[Ejemplo 1. Raíces en intervalo ] [ Ejemplo 2. Raíces en intervalo ] ..
Ejemplo 1 . Raíces en intervalo
Referencia: Burden 7Ed Capítulo 1.1 Ejemplo 2 p11; Burden 9Ed p8
Para la expresión mostrada encuentre una solución en el intervalo [0,1],
x^5 -2x^3 + 3x^2 -1 = 0considere nombrar a la parte izquierda de la ecuación como f(x), para encontrar la solucion como f(x) = 0.
f(x) = x^5 -2x^3 + 3x^2 -1dado que al evaluar en los extremos del intervalo [0,1]:
f(0) = (0)^5 -2(0)3 + 3(0)^2 -1 = -1 f(1) = 1^5 -2(1)^3 + 3(1)^2 -1 = 1Los valores de la función en los extremos son -1 y 1, existe cambio de signo, y dado que f es contínua, por el teorema del valor intermedio existe un valor de x en el intervalo, tal que se satisface que el valor de la función es cero.
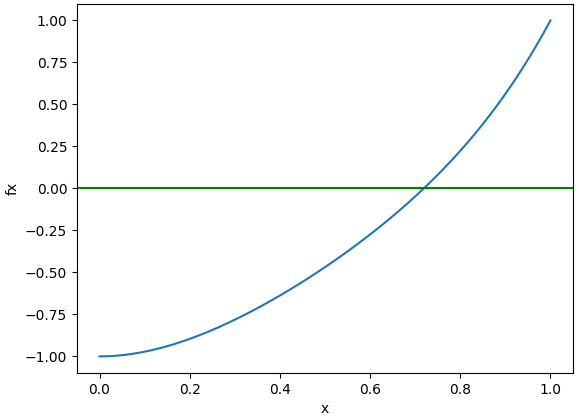
La gráfica de la ecuación muestra el punto o raíz a buscar:
Se pueden dividir en muchas muestras el intervalo x=[a,b] y buscar los puntos xi donde la función f(xi) cambia de signo.
Usando un algoritmo con muestras = 1001 se encuentra que existen dos puntos donde se encuentra la raíz.
raiz entre posiciones i: [ 479. 480.] entre los valores: [ xi, fi] [[ 0.7185 -0.00162876] [ 0.72 0.00219576]]
Algoritmo en Python
En el intervalo [a,b] se crean nuevos puntos de muestras para realizar la gráfica. Las muestras se usan para buscar un nuevo intervalo entre x[i] y x[i+1] donde ocurre un cambio de signo en f(x[i]).
# Burden Capítulo 1.1 Ejemplo 2 p11, pdf 21 # raices del polinomio en [a,b] import numpy as np import matplotlib.pyplot as plt funcionx = lambda x: x**5 - 2*(x**3) + 3*(x**2) -1 # INGRESO a = 0 b = 1.5 muestras = 1001 # PROCEDIMIENTO xi = np.linspace(a,b,muestras) fi = funcionx(xi) # Busca cambios de signo donde=[] # donde[i,xi,fi] for i in range(0,muestras-1,1): antes = fi[i] despues = fi[i+1] signo = (np.sign(antes))*(np.sign(despues)) if (signo<0): donde.append([i,xi[i],antes]) donde.append([i+1,xi[i+1],despues]) donde = np.array(donde) # SALIDA print('raiz entre posiciones i: ', donde[:,0]) print('entre los valores: ') print(' [ xi, fi]') print(donde[:,1:]) # GRAFICA plt.plot(xi,fi) plt.xlabel('x') plt.ylabel('fx') plt.axhline(y=0, color='g') plt.show()
Al observar los resultados, realice sus comentarios y recomendaciones relacionadas con la respuesta obtenida para mejorar la respuesta
Usando Scipy.Optimize
Continuando con el uso de funciones de scipy se obtiene una de las raíces, empezando la búsqueda desde 0.4.
raiz en : [ 0.71913933] >>>
para la otra raíz usar un nuevo punto de partida. Compare respuestas con el método anterior.
las instrucciones usadas son:
# Burden Capítulo 1.1 Ejemplo 2 p11, pdf 21 # raices del polinomio en [a,b] import numpy as np import scipy.optimize as opt fx = lambda x: x**5 - 2*(x**3) + 3*(x**2) -1 # INGRESO a = 0 b = 1.5 x0 = 0.4 # PROCEDIMIENTO # fx pasa por cero, cerca de x0 donde = opt.fsolve(fx,x0) # SALIDA print('raiz en : ', donde)
[Ejemplo 1. Raíces en intervalo ] [ Ejemplo 2. Raíces en intervalo ] ..
Ejemplo 2 . Raíces en intervalo
Referencia: Burden 7Ed cap1.1 Ejercicio 1. p15, Burden 9Ed p15
Demuestre que las siguientes ecuaciones tienen al menos una solución en los intervalos dados
x \cos (x) - 2 x^{2} + 3 x -1 = 0en el intervalo [0.2, 0.3] y [1.2, 1.3]
2.1 Desarrollo analítico
Del «teorema del valor intermedio«, si hay cambio de signo al evaluar la función en los puntos x=0.2 y x=0.3, debe existir un punto c donde se cumple la expresión.
f(x) = x \cos (x) - 2 x^{2} + 3 x -1 f(0.2) = 0.2 \cos (0.2) - 2 (0.2)^2 +3(0.2) -1 = -0.2839 f(0.3) = 0.2 \cos (0.3) - 2 (0.3)^2 +3(0.3) -1 = 0.00660094Hay cambio de signo de la función en el intervalo, por lo que la ecuación debe pasar por cero, y se cumple la igualdad.
2.2 Desarrollo numérico con Python
Por simplicidad se usa la ventana iterativa. Se evalúa la función en los puntos extremos del intervalo y con los resultados se continúa de forma semejante a la sección de desarrollo analítico.
>>> import numpy as np >>> fx = lambda x: x*np.cos(x) - 2*(x**2) + 3*x -1 >>> fx(0.2) -0.28398668443175157 >>> fx(0.3) 0.0066009467376817454
es decir, por cambio de signo, debe haber un cruce por cero de la función en el intervalo.
2.3 Desarrollo con gráfica
Como existen varios intervalos, [0.2, 0.3] y [1.2, 1.3] se unifican los intervalos entre los extremos x=[0.2, 1.3].
Para la gráfica se crean 100 tramos (pasos o divisiones) en el intervalo que equivalen a 101 muestras en el intervalo
>>> muestras=101 >>> xi = np.linspace(0.2,1.3,muestras) >>> fi = fx(xi) >>> xi array([ 0.2 , 0.211, 0.222, 0.233, 0.244, 0.255, 0.266, 0.277, ... 1.256, 1.267, 1.278, 1.289, 1.3 ]) >>> fi array([-0.28398668, -0.24972157, -0.21601609, -0.18287411, -0.15029943, ..., -0.13225152])
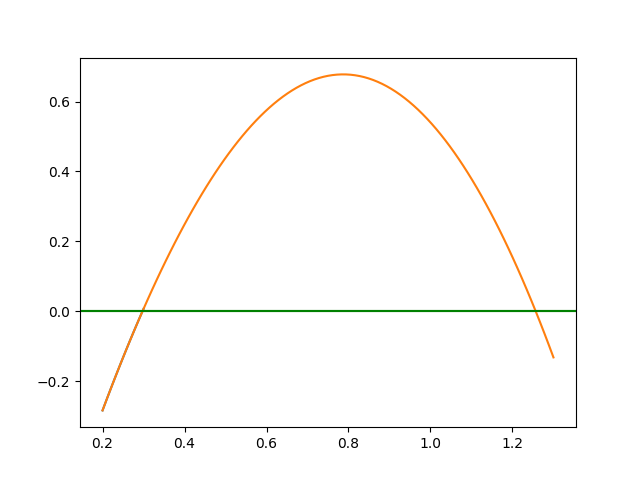
Una gráfica permite observar mejor la función en el intervalo.
Se necesita llamar a la librería matplotlib.pyplot que se resume como plt.
>>> import matplotlib.pyplot as plt >>> plt.plot(xi,fi) [<matplotlib.lines.Line2D object at 0x0000020C67820E80>] >>> plt.axhline(0,color='g') <matplotlib.lines.Line2D object at 0x0000020C678204E0> >>> plt.show()
plt.plot() crea la gráfica con los vectores xi y fi , añadiendo como referencia en este caso una linea horizontal que pasa por cero, usando plt.axhline(). Finalmente se muestra la gráfica con plt.show().
De la gráfica, fácilmente se puede observar que existen dos puntos «c» que cumplen con la igualdad y que se encuentran en los intervalos de evaluación, con lo que se comprueba que existe solución en los intervalos presentados en el problema.
Resumen de instrucciones Python
# Raices en intervalo - Ejemplo02 import numpy as np import matplotlib.pyplot as plt fx = lambda x: x*np.cos(x) - 2*(x**2) + 3*x -1 # INGRESO a = 0.2 b = 1.3 muestras = 101 # PROCEDIMIENTO xi = np.linspace(a,b,muestras) fi = fx(xi) # SALIDA - GRAFICA plt.plot(xi,fi) plt.axhline(0,color='g') plt.show()
Tarea: continúe con el ejercicio usando la función de scipy.optimize.fsolve() y compare resultados.
[Ejemplo 1. Raíces en intervalo ] [ Ejemplo 2. Raíces en intervalo ]
3. Tarea
Continuar con el ejercicio observando que si el dominio es [-2,2] se tiene que:

gráfica obtenida con:
# Burden Capítulo 1.1 Ejemplo 2 p11, pdf 21 # raices del polinomio en [a,b] import numpy as np import matplotlib.pyplot as plt funcionx = lambda x: x**5 - 2*(x**3) + 3*(x**2) -1 # INGRESO a = -2 b = 2 muestras = 1001 # PROCEDIMIENTO xi = np.linspace(a,b,muestras) yi = funcionx(xi) # SALIDA plt.plot(xi,yi) plt.axhline(0, color='green') plt.axvline(0, color='green') plt.show()
[Ejemplo 1. Raíces en intervalo ] [ Ejemplo 2. Raíces en intervalo ]