Referencia: Burden 9Ed. ejemplo 1 p50
La ecuación mostrada tiene una raiz en [1,2], ya que f(1)=-5 y f(2)=14 y existe cambio de signo. Muestre los resultados parciales del algoritmo de la bisección con una tolerancia de 0.0001
f(x) = x^3 + 4x^2 -10 =0Desarrollo Analítico
Como parte del desarrollo del ejercicio se presenta las iteraciones para el algoritmo, tradicionalmente realizadas con una calculadora.
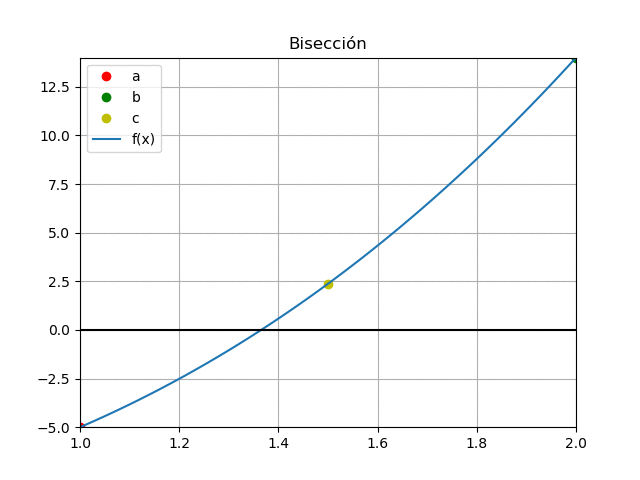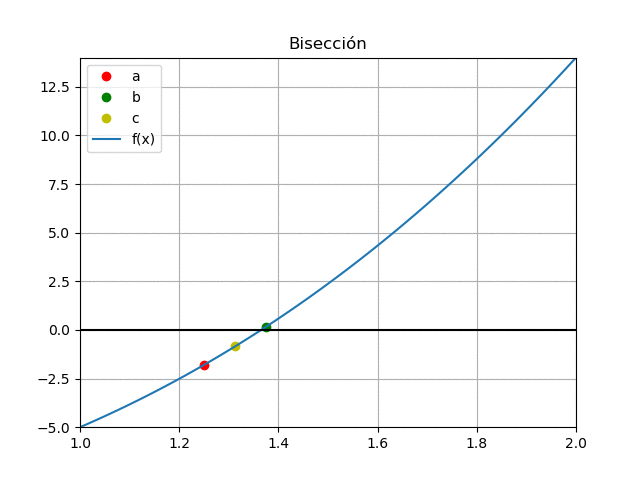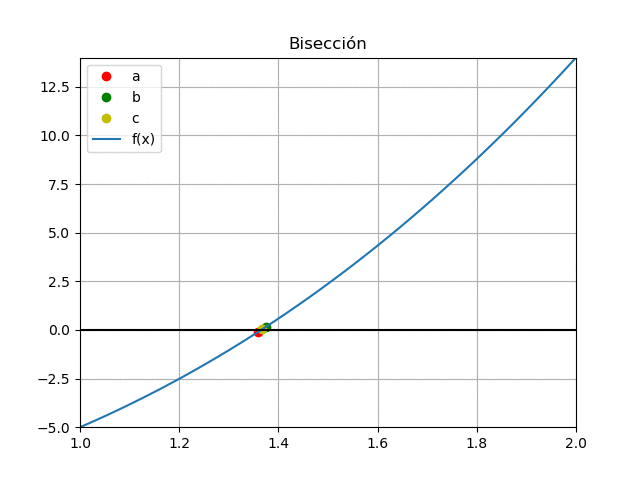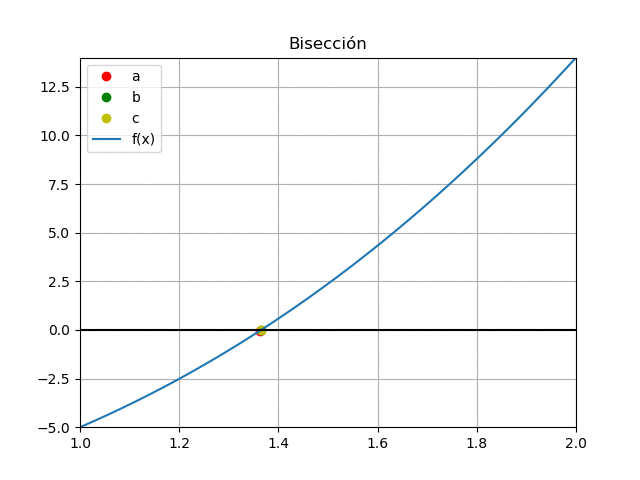
iteración 1
a = 1, b=2 c = \frac{a+b}{2} = \frac{1+2}{2} = 1.5 f(1) = (1)^3 + 4(1)^2 -10 = -5 f(1.5) = (1.5)^3 + 4(1.5)^2 -10= 2.37 f(2) = (2)^3 + 4(2)^2 -10 =14 tramo = 2-1 =1cambio de signo a la izquierda
a = 1, b= c = 1.5iteración 2
a = 1, b=1.5 c = \frac{1+1.5}{2} = 1.25 f(1) = -5 f(1.25) = (1.25)^3 + 4(1.25)^2 -10 = -1.794 f(1.5) = 2.37 tramo = 1.5-1 = 0.5cambio de signo a la derecha
a = c = 1.25, b=1.5iteración 3
continuar como tarea.
La tabla resume los valores de las iteraciones
| i | a | c | b | f(a) | f(c) | f(b) | tramo |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1.5 | 2 | -5 | 2.37 | 14 | 1 |
| 2 | 1 | 1.25 | 1.5 | -5 | -1.794 | 2.37 | 0.5 |
| 3 | 1.25 | … | 1.5 |
La misma tabla se puede relizar con un algoritmo para tener los resultados más rápido y observar el comportamiento del método.
Observe los resultados de f(c), principalmente en la iteracion i=9 con tramo=0.004, respecto a la obtenida en la última iteración.
[i, a, c, b, f(a), f(c), f(b), tramo] 1 1.000 1.500 2.000 -5.000 2.375 14.000 1.000 2 1.000 1.250 1.500 -5.000 -1.797 2.375 0.500 3 1.250 1.375 1.500 -1.797 0.162 2.375 0.250 4 1.250 1.312 1.375 -1.797 -0.848 0.162 0.125 5 1.312 1.344 1.375 -0.848 -0.351 0.162 0.062 6 1.344 1.359 1.375 -0.351 -0.096 0.162 0.031 7 1.359 1.367 1.375 -0.096 0.032 0.162 0.016 8 1.359 1.363 1.367 -0.096 -0.032 0.032 0.008 9 1.363 1.365 1.367 -0.032 0.000 0.032 0.004 10 1.363 1.364 1.365 -0.032 -0.016 0.000 0.002 11 1.364 1.365 1.365 -0.016 -0.008 0.000 0.001 raiz: 1.36474609375 >>>
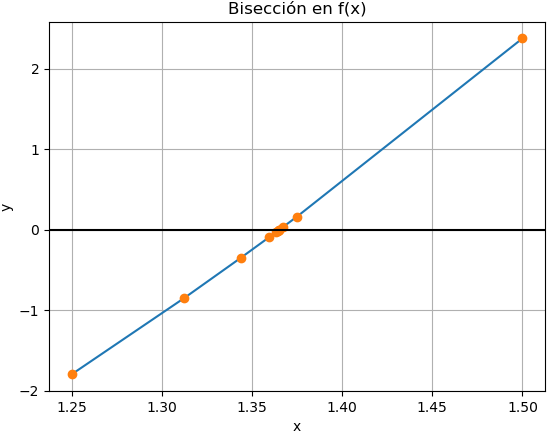
Se grafican los puntos [c,f(c)] de la tabla para obsevar el resultado de forma gráfica, resaltando que los puntos al final se aglomeran alrededor de la solución o raiz de la ecuación.
Escriba sus observaciones y preguntas sobre los resultados.
Algoritmo en Python
El video presenta el desarrollo básico conceptual del algoritmo en Python para una comprensión del proceso de creación algoritmica.
Algoritmo básico del video
# Algoritmo de Bisección # [a,b] se escogen de la gráfica de la función # error = tolera import numpy as np import matplotlib.pyplot as plt # INGRESO fx = lambda x: x**3 + 4*x**2 - 10 a = 1 b = 2 tolera = 0.001 # PROCEDIMIENTO tramo = b-a while not(tramo<tolera): c = (a+b)/2 fa = fx(a) fb = fx(b) fc = fx(c) cambia = np.sign(fa)*np.sign(fc) if cambia < 0: a = a b = c if cambia > 0: a = c b = b tramo = b-a # SALIDA print(' raiz en: ', c) print('error en tramo: ', tramo)
Mejorando el algoritmo
El algoritmo presentado en el video se puede mejorar, por ejemplo simplificando los dos condicionales en uno.
Considere que siempre se evalúa la función en tres puntos y se puede optimizar sustituyendo los valores de los extremos y solo evaluando el centro.
El resultado se mejorar usando los valores finales del último intervalo [a,b] y obteniendo una nueva midad ‘c’ al final.
Para mostrar la tabla de la sección anterior se agregan los resultados parciales a una tabla que permita mostrar el resultado al final
# Algoritmo de Bisección # [a,b] se escogen de la gráfica de la función # error = tolera import numpy as np # INGRESO fx = lambda x: x**3 + 4*x**2 - 10 a = 1 b = 2 tolera = 0.001 # PROCEDIMIENTO tabla = [] tramo = b-a fa = fx(a) fb = fx(b) i = 1 while (tramo>tolera): c = (a+b)/2 fc = fx(c) tabla.append([i,a,c,b,fa,fc,fb,tramo]) i = i + 1 cambia = np.sign(fa)*np.sign(fc) if (cambia<0): b = c fb = fc else: a=c fa = fc tramo = b-a c = (a+b)/2 fc = fx(c) tabla.append([i,a,c,b,fa,fc,fb,tramo]) tabla = np.array(tabla) raiz = c # SALIDA np.set_printoptions(precision = 4) print('[ i, a, c, b, f(a), f(c), f(b), tramo]') # print(tabla) # Tabla con formato n=len(tabla) for i in range(0,n,1): unafila = tabla[i] formato = '{:.0f}'+' '+(len(unafila)-1)*'{:.3f} ' unafila = formato.format(*unafila) print(unafila) print('raiz: ',raiz)
El ultimo complemento al algoritmo consiste en realizar la gráfica, seleccionando solo las columnas correspondientes a [c,f(c)].
Se ordenan los datos en forma ascendente antes de graficarlos usando solo sus índices con np.argsort(xi)
# Algoritmo de Bisección # GRAFICA import matplotlib.pyplot as plt xi = tabla[:,2] yi = tabla[:,5] # ordena los puntos para la grafica orden = np.argsort(xi) xi = xi[orden] yi = yi[orden] plt.plot(xi,yi) plt.plot(xi,yi,'o') plt.axhline(0, color="black") plt.xlabel('x') plt.ylabel('y') plt.title('Bisección en f(x)') plt.grid() plt.show()
Scipy.optimize.bisect
El método de la bisección se encuentra también implementado en las libreria Scipy, que también puede ser usado de la forma:
>>> import scipy.optimize as opt >>> opt.bisect(fx,1,2,xtol=0.001) 1.3642578125
que es el valor de la variable ‘a’ de la tabla para la última iteración del ejercicio. Lo que muestra que el algoritmo realizado tiene un valor más aproximado.
Sin embargo por didáctica y mejor comprensión de los métodos y su implementación en algoritmos que es parte del objetivo de aprendizaje, se continuará desarrollando la forma básica en Python.
Referencia: https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.bisect.html