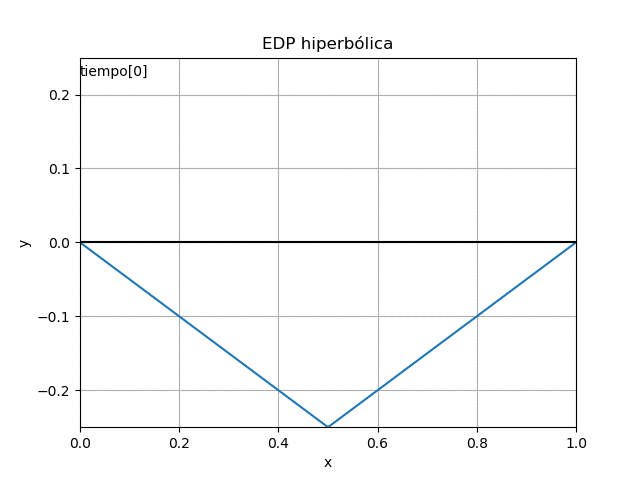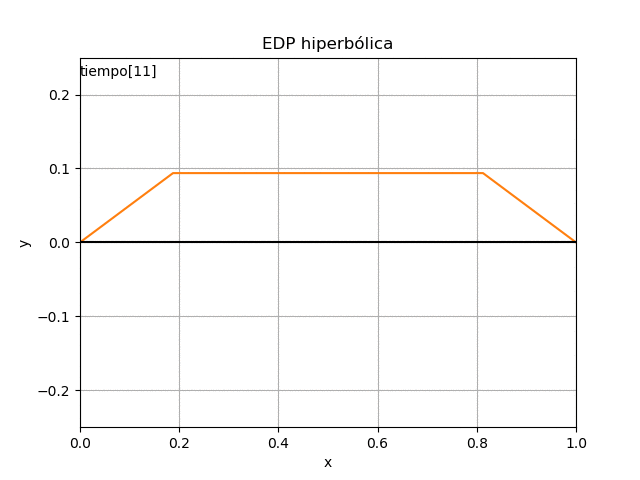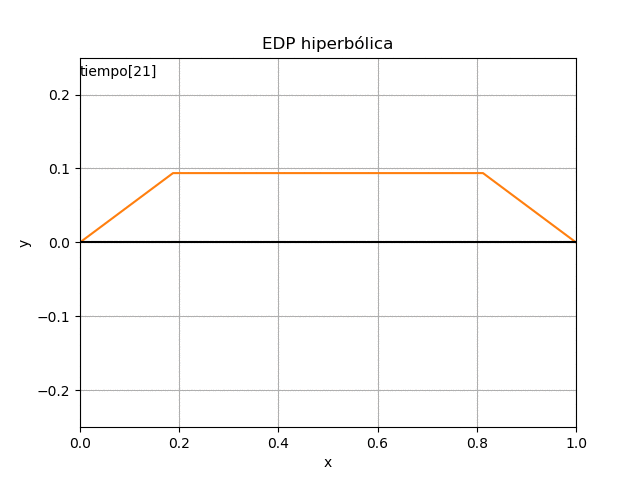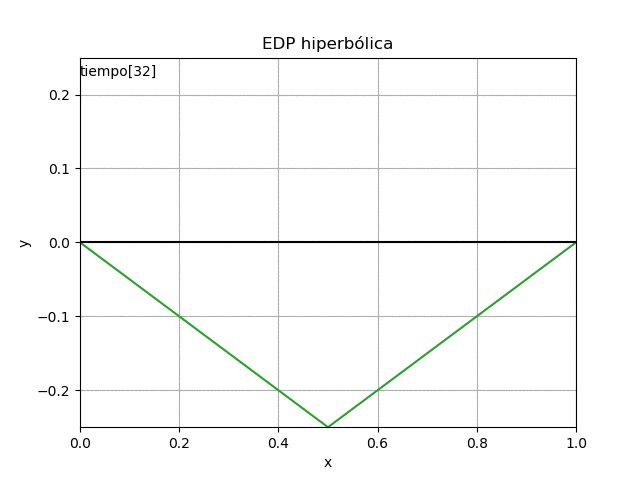
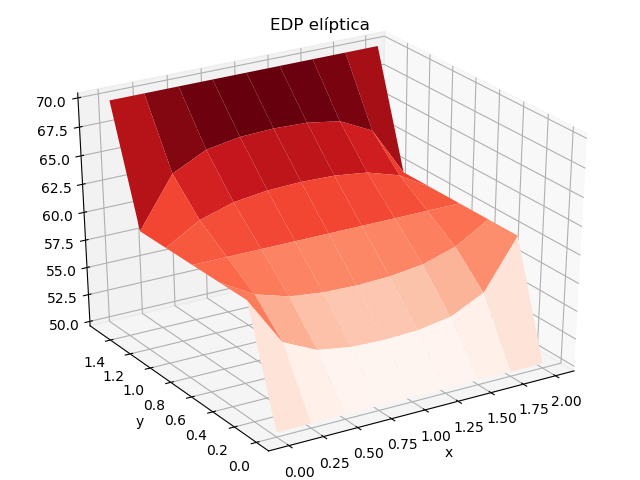
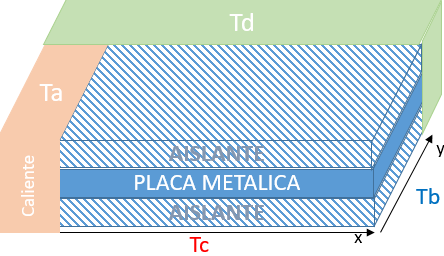
con el resultado desarrollado en EDP elípticas para:
\frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{ \partial y^2} = 0
y con el supuesto que: \lambda = \frac{(\Delta y)^2}{(\Delta x)^2} = 1
se puede plantear que:
u_{i+1,j}-4u_{i,j}+u_{i-1,j} + u_{i,j+1} +u_{i,j-1} = 0
con lo que para el método implícito, se plantea un sistema de ecuaciones para determinar los valores en cada punto desconocido.
j=1, i =1
u_{2,1}-4u_{1,1}+u_{0,1} + u_{1,2} +u_{1,0} = 0
u_{2,1}-4u_{1,1}+Ta + u_{1,2} +Tc= 0
-4u_{1,1}+u_{2,1}+u_{1,2} = -(Tc+Ta)
j=1, i =2
u_{3,1}-4u_{2,1}+u_{1,1} + u_{2,2} +u_{2,0} = 0
u_{3,1}-4u_{2,1}+u_{1,1} + u_{2,2} +Tc = 0
u_{1,1}-4u_{2,1}+u_{3,1}+ u_{2,2}= -Tc
j=1, i=3
u_{4,1}-4u_{3,1}+u_{2,1} + u_{3,2} +u_{3,0} = 0
Tb-4u_{3,1}+u_{2,1} + u_{3,2} +Tc = 0
u_{2,1} -4u_{3,1} + u_{3,2} = -(Tc+Tb)
j=2, i=1
u_{2,2}-4u_{1,2}+u_{0,2} + u_{1,3} +u_{1,1} = 0
u_{2,2}-4u_{1,2}+Ta + u_{1,3} +u_{1,1} = 0
-4u_{1,2}+u_{2,2}+u_{1,1}+u_{1,3} = -Ta
j = 2, i = 2
u_{1,2}-4u_{2,2}+u_{3,2} + u_{2,3} +u_{2,1} = 0
j = 2, i = 3
u_{4,2}-4u_{3,2}+u_{2,2} + u_{3,3} +u_{3,1} = 0
Tb-4u_{3,2}+u_{2,2} + u_{3,3} +u_{3,1} = 0
u_{2,2} -4u_{3,2}+ u_{3,3} +u_{3,1} = -Tb
j=3, i = 1
u_{2,3}-4u_{1,3}+u_{0,3} + u_{1,4} +u_{1,2} = 0
u_{2,3}-4u_{1,3}+Ta + Td +u_{1,2} = 0
-4u_{1,3}+u_{2,3}+u_{1,2} = -(Td+Ta)
j=3, i = 2
u_{3,3}-4u_{2,3}+u_{1,3} + u_{2,4} +u_{2,2} = 0
u_{3,3}-4u_{2,3}+u_{1,3} + Td +u_{2,2} = 0
+u_{1,3} -4u_{2,3}+u_{3,3} +u_{2,2} = -Td
j=3, i=3
u_{4,3}-4u_{3,3}+u_{2,3} + u_{3,4} +u_{3,2} = 0
Tb-4u_{3,3}+u_{2,3} + Td +u_{3,2} = 0
u_{2,3}-4u_{3,3}+u_{3,2} = -(Td+Tb)
con las ecuaciones se arma una matriz:
A = np.array([
[-4, 1, 0, 1, 0, 0, 0, 0, 0],
[ 1,-4, 1, 0, 1, 0, 0, 0, 0],
[ 0, 1,-4, 0, 0, 1, 0, 0, 0],
[ 1, 0, 0,-4, 1, 0, 1, 0, 0],
[ 0, 1, 0, 1,-4, 1, 0, 1, 0],
[ 0, 0, 1, 0, 1,-4, 0, 0, 1],
[ 0, 0, 0, 1, 0, 0,-4, 1, 0],
[ 0, 0, 0, 0, 1, 0, 1,-4, 1],
[ 0, 0, 0, 0, 0, 1, 0, 1,-4],
])
B = np.array([-(Tc+Ta),-Tc,-(Tc+Tb),
-Ta, 0, -Tb,
-(Td+Ta),-Td,-(Td+Tb)])
que al resolver el sistema de ecuaciones se obtiene:
>>> Xu
array([ 56.43, 55.71, 56.43, 60. , 60. , 60. , 63.57, 64.29,
63.57])
ingresando los resultados a la matriz u:
xi=
[ 0. 0.5 1. 1.5 2. ]
yj=
[ 0. 0.38 0.75 1.12 1.5 ]
matriz u
[[ 60. 60. 60. 60. 60. ]
[ 50. 56.43 60. 63.57 70. ]
[ 50. 55.71 60. 64.29 70. ]
[ 50. 56.43 60. 63.57 70. ]
[ 60. 60. 60. 60. 60. ]]
>>>
Algoritmo usado para resolver el problema:
# Ecuaciones Diferenciales Parciales
# Elipticas. Método implícito
import numpy as np
# INGRESO
# Condiciones iniciales en los bordes
Ta = 60
Tb = 60
Tc = 50
Td = 70
# dimensiones de la placa
x0 = 0
xn = 2
y0 = 0
yn = 1.5
# discretiza, supone dx=dy
tramosx = 4
tramosy = 4
dx = (xn-x0)/tramosx
dy = (yn-y0)/tramosy
maxitera = 100
tolera = 0.0001
A = np.array([
[-4, 1, 0, 1, 0, 0, 0, 0, 0],
[ 1,-4, 1, 0, 1, 0, 0, 0, 0],
[ 0, 1,-4, 0, 0, 1, 0, 0, 0],
[ 1, 0, 0,-4, 1, 0, 1, 0, 0],
[ 0, 1, 0, 1,-4, 1, 0, 1, 0],
[ 0, 0, 1, 0, 1,-4, 0, 0, 1],
[ 0, 0, 0, 1, 0, 0,-4, 1, 0],
[ 0, 0, 0, 0, 1, 0, 1,-4, 1],
[ 0, 0, 0, 0, 0, 1, 0, 1,-4],
])
B = np.array([-(Tc+Ta),-Tc,-(Tc+Tb),
-Ta,0,-Tb,
-(Td+Ta),-Td,-(Td+Tb)])
# PROCEDIMIENTO
# Resuelve sistema ecuaciones
Xu = np.linalg.solve(A,B)
[nx,mx] = np.shape(A)
xi = np.arange(x0,xn+dx,dx)
yj = np.arange(y0,yn+dy,dy)
n = len(xi)
m = len(yj)
u = np.zeros(shape=(n,m),dtype=float)
u[:,0] = Tc
u[:,m-1] = Td
u[0,:] = Ta
u[n-1,:] = Tb
u[1:1+3,1] = Xu[0:0+3]
u[1:1+3,2] = Xu[3:3+3]
u[1:1+3,3] = Xu[6:6+3]
# SALIDA
np.set_printoptions(precision=2)
print('xi=')
print(xi)
print('yj=')
print(yj)
print('matriz u')
print(u)
La gráfica de resultados se obtiene de forma semejante al ejercicio con método iterativo.
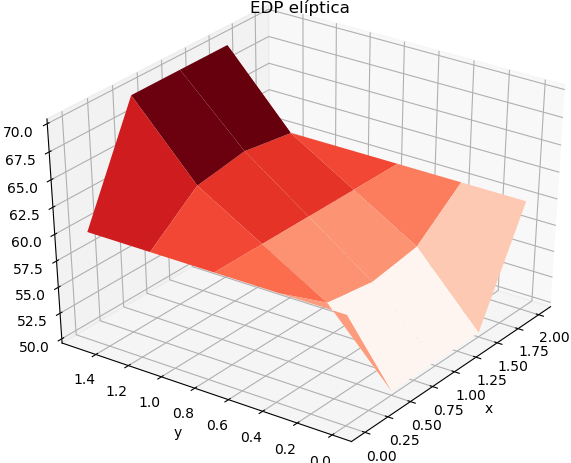
# Gráfica
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
X, Y = np.meshgrid(xi, yj)
U = np.transpose(u) # ajuste de índices fila es x
figura = plt.figure()
ax = Axes3D(figura)
ax.plot_surface(X, Y, U, rstride=1, cstride=1, cmap=cm.Reds)
plt.title('EDP elíptica')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
Se podría estandarizar un poco más el proceso para que sea realizado por el algoritmo y sea más sencillo generar la matriz con más puntos. Tarea.