Categoría: Soluciones

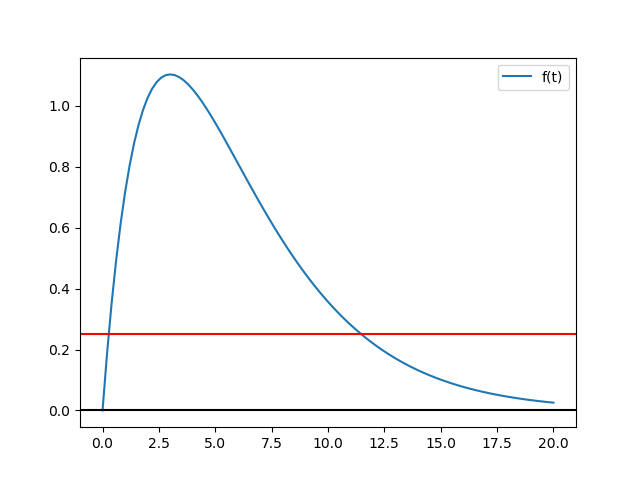
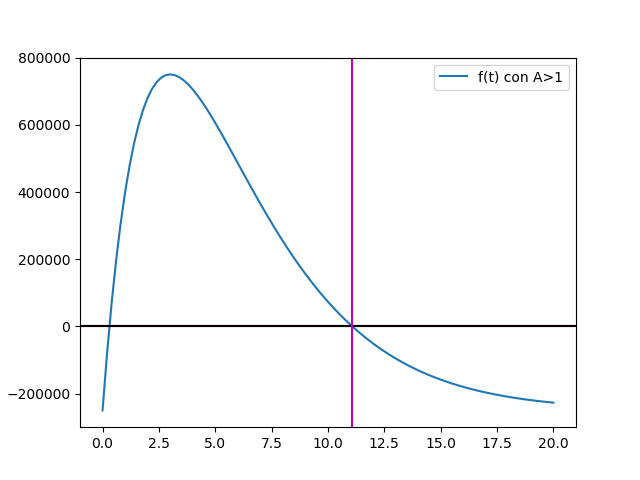
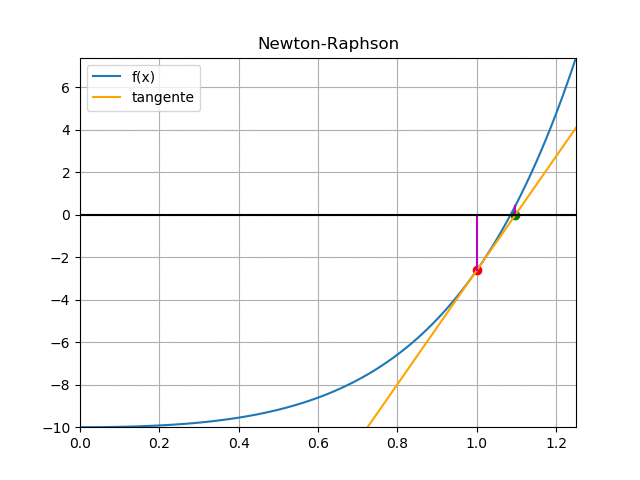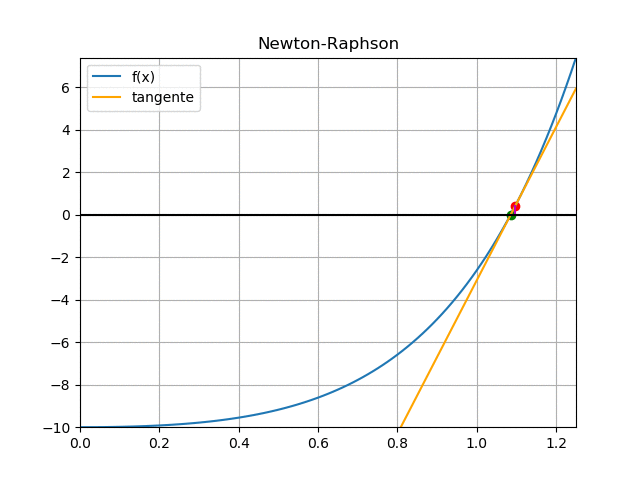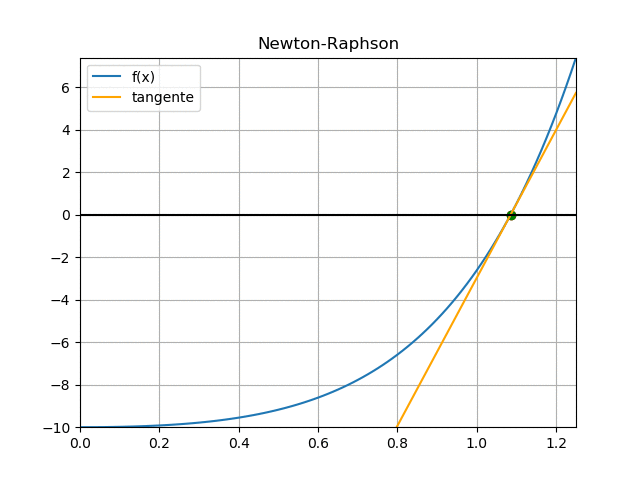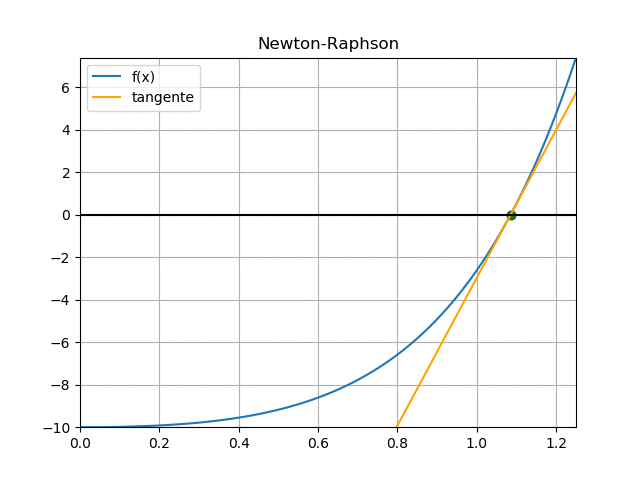
Ejercicio: 1Eva_IT2011_T3_MN Precios unitarios en factura, k

Las ecuaciones basadas en las sumas de cantidad.preciounitario representan el valor pagado en cada factura.

Siendo X_i el precio unitario de cada material:

2x_1 + 5x_2 + 4x_3 = 35 3x_1 + 9x_2 + 8x_3 = k 5x_1 + 3x_2 + x_3 = 17

se escriben en la forma matricial Ax=B

\begin{bmatrix} 2 && 5 && 4 \\ 3 && 9 && 8 \\ 5 && 3 && 1 \end{bmatrix}.\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}=\begin{bmatrix} 35 \\ k \\ 17 \end{bmatrix}

luego se escribe la matriz aumentada:

\begin{bmatrix} 2 && 5 && 4 && 35\\ 3 && 9 && 8 && k\\ 5 && 3 && 1 && 17\end{bmatrix}

se pivotea por filas buscando tener una matriz diagonal dominante,

\begin{bmatrix} 5 && 3 && 1 && 17 \\ 3 && 9 && 8 && k\\ 2 && 5 && 4 && 35\\\end{bmatrix}

Luego se usa el procedimiento de eliminación hacia adelante,

\begin{bmatrix} 5 && 3 && 1 && 17 \\ 3-5\frac{3}{5} && 9-3\frac{3}{5} && 8-1\frac{3}{5} && k-17\frac{3}{5} \\ 2-5\frac{2}{5} && 5-3\frac{2}{5} && 4-1\frac{2}{5} && 35-17\frac{2}{5} \end{bmatrix} \begin{bmatrix} 5 && 3 && 1 && 17 \\ 0 && \frac{36}{5} && \frac{37}{5} && k-\frac{51}{5} \\ 0 && \frac{19}{5} && \frac{18}{5} && \frac{141}{5} \end{bmatrix} \begin{bmatrix} 5 && 3 && 1 && 17 \\ 0 && 36 && 37 && 5k-51 \\ 0 && 19 && 18 && 141 \end{bmatrix} \begin{bmatrix} 5 && 3 && 1 && 17 \\ 0 && 36 && 37 && 5k-51 \\ 0 && 19-36\frac{19}{36} && 18-37\frac{19}{36} && 141-(5k-51)\frac{19}{36} \end{bmatrix} \begin{bmatrix} 5 && 3 && 1 && 17 \\ 0 && 36 && 37 && 5k-51 \\ 0 && 0 && \frac{-55}{36} && \frac{6045-5k}{36} \end{bmatrix}

multiplicando la última fila por 36,

\begin{bmatrix} 5 && 3 && 1 && 17 \\ 0 && 36 && 37 && 5k-51 \\ 0 && 0 && -55 && 6045-5k \end{bmatrix}

con lo que se pueden obtener cada precio unitario en función de k.
Como variante, se continua siguiendo el procedimieno de Gauss, dejando como tarea el uso de Gauss-Jordan

-55x_3 = 6045-5k x_3 = -\frac{6045-5k}{55} 36 x_2 + 37 x_3 = 5k-51 x_2 = \frac{1}{36}(5k-51 - 37 x_3) x_2 = \frac{1}{36} \Big( 5k-51 - 37 \big(-\frac{6045-5k}{55}\big) \Big) 5x_1 + 3 x_2 +x_3 = 17 x_1 = \frac{1}{5} \Big[ 17 - 3 x_2 - x_3 \Big] x_1 = \frac{1}{5} \Big[17-3\frac{1}{36} \Big( 5k-21 - 37 \big(-\frac{6045-5k}{55}\big) \Big) - \Big( -\frac{6045-5k}{55} \Big) \Big]

para luego simplificar las expresiones (tarea).

En el literal c se indica que el valor de k es 65, con lo que se requiere sustituir en la solución el valor de K para encontrar los precios unitarios.

\begin{bmatrix} 5 && 3 && 1 && 17 \\ 3 && 9 && 8 && 65\\ 2 && 5 && 4 && 35\\\end{bmatrix}

Se encuentra que:

el vector solución X es:

[[-0.18181818]
 [ 5.18181818]
 [ 2.36363636]]

Lo que muestra que debe existir un error en el planteamiento del enunciado, considerando que los precios NO deberían ser negativos como sucede con el primer precio unitario de la respuesta.

que es lo que suponemos ser trata de corregir en el literal d, al indicar que se cambie en la matriz el valor de 5 por 5.1. Los resultados en éste caso son más coherentes con el enunciado. Todas las soluciones son positivas.

A = np.array([[ 5.1, 3  , 1],
              [ 3. , 9  , 8],
              [ 2. , 5.1, 4]])
B1 = np.array([ 17, 65, 35])

el vector solución X es:
[[0.33596838]
 [3.88669302]
 [3.62648221]]

El error relativo de los precios encontrados entre las ecuaciones planteadas es:

diferencia = [0.335968-0.181818,
              3.886693-5.181818, 
              3.626482-2.363636]
           = [0.154150, -1.295125, 1.262845]
error(dolares) = max|diferencia| = 1.295125
Por las magnitudes de los precios, el error se aprecia
usando el error relativo referenciado 
al mayor valor de la nueva solución
error relativo = 1.295125/3.886693 = 0.333220
es decir de aproximadamente 33%

Para revisar otra causa del error se analiza el número de condición de la matriz:

>>> A
array([[5.1, 3. , 1. ],
       [3. , 9. , 8. ],
       [2. , 5.1, 4. ]])
>>> np.linalg.cond(A)
60.28297696795716

El número de condición resulta lejano a 1, por lo que para éste problema:
pequeños cambios en la matriz de entrada producen grandes cambios en los resultados.

por ejemplo: un 0.1/5= 0.02 que es un 2% de variación en la entrada produce un cambio del 33% en el resultado.

Ejercicio: 1Eva_IT2011_T1_MN Fondo de inversión

Se desarrolla para la función:

C(t)=Ate^{-t/3}

siguiento las instrucciones por partes, se obtienen los siguientes resultados:
los valores resultantes:

derivada de la función: 
-x*exp(-x/3)/3 + exp(-x/3)
valor maximo en : 
3.0000001192092896
A para un millon: 
906093.94282
el valor de t para la meta es: 
11.0779035867

las instrucciones en python para observar la función son:

# 1ra Evaluación I Término 2011
# Tema 1. Fondo de Inversion
import numpy as np
import matplotlib.pyplot as plt

ft = lambda t: t*np.exp(-t/3)

a=0
b=20
tolera = 0.000001
muestras = 101
meta = 0.25
# PROCEDIMIENTO
# Observar la función entre [a,b]
ti = np.linspace(a,b,muestras)
fti = ft(ti)

# Salida
# Gráfica
plt.plot(ti,fti, label='f(t)')
plt.axhline(meta, color = 'r')
plt.axhline(0, color = 'k')
plt.legend()
plt.show()

Para desarrollar el literal a), donde se busca el valor máximo, usando la derivada de la función cuando existe el cruce por cero.
Para la derivada se usa la forma simbólica de la función, que se convierte a forma numérica lambda para evaluarla de forma más fácil.

# Literal a) usando derivada simbólica
import sympy as sp
x = sp.Symbol('x')
fxs = x*sp.exp(-x/3)
dfxs = fxs.diff(x,1)

# convierte la expresión a lambda
dfxn = sp.utilities.lambdify(x,dfxs,'numpy')
dfxni = dfxn(ti)
print('derivada de la función: ')
print(dfxs)
# Gráfica de la derivada.
plt.plot(ti,dfxni, label='df(t)/dt')
plt.axhline(0, color = 'k')
plt.legend()
plt.show()

derivada de la función: 
-x*exp(-x/3)/3 + exp(-x/3)

Se busca la raiz con algún método, por ejemplo bisección.

# Busca el máximo en dfxni
def biseccion(funcionx,a,b,tolera):
    fa = funcionx(a)
    fb = funcionx(b)
    tramo = np.abs(b-a)
    while (tramo>=tolera):
        c = (a+b)/2
        fc = funcionx(c)
        cambia = np.sign(fa)*np.sign(fc)
        if (cambia<0):
            b = c
            fb = fc
        else:
            a = c
            fa = fc
        tramo = np.abs(b-a)
    return(c)

# usa función para encontrar el máximo
raizmax = biseccion(dfxn, a, b, tolera)
verifica =  dfxn(raizmax)
print('valor maximo en : ')
print(raizmax)

# que el máximo sea un millon
tmax = raizmax
A = (1000000)/ft(tmax)
print('A para un millon: ')
print(A)

valor maximo en : 3.0000001192092896
A para un millon: 906093.94282

Para el literal b, se busca la laiz usando el metodo de Newton-Raphson como se indica en el enunciado.
En la función nueva se usa el valor de A encontrado, y la meta establecida.
Se obtiene la misa derivada del problema anterio multiplicada por A, por ser solo un factor que multiplica a la función original. El valor de meta es una constante, que se convierte en cero al derivar.

# literal b), buscar cumplir meta de 0.25 millones
def newtonraphson(funcionx, fxderiva, c, tolera):
    tramo = abs(2*tolera)
    while (tramo>=tolera):
        xnuevo = c - funcionx(c)/fxderiva(c)
        tramo = abs(xnuevo-c)
        c = xnuevo
    return(c)

ft1 = lambda t: A*t*np.exp(-t/3) - 250000
# usar método de newton,
# puede usar la misma derivada multiplicada por A
dft1s = A*(fxs.diff(x,1))
dft1 = sp.utilities.lambdify(x,dft1s,'numpy')
c = 10

raiz4 = newtonraphson(ft1, dft1, c, tolera)
ft1i = ft1(ti)

print('el valor de t para la meta es: ')
print(raiz4)

# Gráfica
plt.plot(ti,ft1i, label = 'f(t) con A>1')
plt.axhline(meta, color = 'r')
plt.axhline(0, color = 'k')
plt.axvline(raiz4, color = 'm')
plt.legend()
plt.show()

el valor de t para la meta es: 11.0779035867

Ejercicio: 1Eva_IT2011_T1 Encontrar α en integral

Desarrollo Analítico

Se iguala la ecuación al valor buscado = 10, y se resuelve

\int_{\alpha}^{2\alpha} x e^{x}dx = 10

siendo: μ = x , δv = e^x, δu = δx , v = e^x

\int u dv = uv - \int v \delta u xe^x \Big|_{\alpha}^{2 \alpha} - \int_{\alpha}^{2\alpha} e^{x}dx - 10 = 0 2\alpha e^{2 \alpha} -\alpha e^{\alpha} - (e^{2\alpha} - e^{\alpha}) - 10 = 0 (2\alpha-1)e^{2 \alpha}+ (1-\alpha) e^{\alpha} - 10 = 0

la función a usar en el método es

f(\alpha) = (2\alpha-1)e^{2 \alpha}+ (1-\alpha)e^{\alpha} -10

Se obtiene la derivada para el método de Newton Raphson

f'(\alpha) = 2e^{2 \alpha} + 2(2\alpha-1)e^{2 \alpha} - e^{\alpha} + (1-\alpha) e^{\alpha} f'(\alpha) = (2 + 2(2\alpha-1))e^{2 \alpha} +(-1 + (1-\alpha)) e^{\alpha} f'(\alpha) = 4\alpha e^{2 \alpha} -\alpha e^{\alpha}

la fórmula para el método de Newton-Raphson

\alpha_{i+1} = \alpha_i - \frac{f(\alpha)}{f'(\alpha)}

se prueba con α₀ = 1, se evita el valor de cero por la indeterminación que se da por f'(0) = 0

iteración 1:

f(1) = (2(1)-1)e^{2(1)}+ (1-(1))e^{(1)} -10 f'(1) = 4(1) e^{2 (1)} -(1) e^{(1)} \alpha_{1} = 1- \frac{f(1)}{f'(1)}

\alpha_{1} = 1.0973
error = 0.0973

iteración 2:
f(2) = (2(1.0973)-1)e^{2(1.0973)}+ (1-(1.0973))e^{(1.0973)} -10

f'(2) = 4(1.0973) e^{2 (1.0973)} -(1.0973) e^{(1.0973)} \alpha_{2} = 1.0973 - \frac{f(1.0973)}{f'(1.0973)}

\alpha_{2} = 1.0853
error = 0.011941

iteración 3:
f(3) = (2(1.0853)-1)e^{2(1.0853)}+ (1-(1.0853))e^{(1.0853)} -10

f'(3) = 4(1.0853) e^{2 (1.0853)} -(1.0853) e^{(1.0853)} \alpha_{3} = 1.0853- \frac{f(1.0853)}{f'(1.0853)}

\alpha_{3} = 1.0851
error = 0.00021951

[  xi,          xnuevo,      f(xi),      f'(xi),       tramo ]
[  1.           1.0973      -2.6109      26.8379       0.0973]
[  1.0973e+00   1.0853e+00   4.3118e-01   3.6110e+01   1.1941e-02]
[  1.0853e+00   1.0851e+00   7.6468e-03   3.4836e+01   2.1951e-04]
[  1.0851e+00   1.0851e+00   2.5287e-06   3.4813e+01   7.2637e-08]
raiz:  1.08512526549

se obtiene el valor de la raíz con 4 iteraciones, con error de aproximación de 7.2637e-08

Desarrollo con Python

Ejercicio: 1Eva_IT2010_T2_MN Uso de televisores

El enunciado indica encontrar el máximo y luego el mínimo, por lo que la curva bajo análisis es la derivada de la función dp(x)/dx.

Adicionalmente, para encontrar los puntos se requiere usar el método de Newton-Raphson que corresponden a las raíces de dp(x)/dx. La función bajo análisis ahora es la derivada y para el método se su la derivada: d²p(x)/dx².

Al usar el computador para las fórmulas, se usa la forma simbólica de la función p(x), para obtener dpx y d2px.

primera derivada: 
-3.13469387755102*x*exp(-8*x/7) + 2.74285714285714*exp(-8*x/7) + 13.7142857142857*exp(-24*x/7)*sin(12*x/7) - 6.85714285714286*exp(-24*x/7)*cos(12*x/7)
segunda derivada: 
(3.58250728862974*x - 6.26938775510204 - 35.265306122449*exp(-16*x/7)*sin(12*x/7) + 47.0204081632653*exp(-16*x/7)*cos(12*x/7))*exp(-8*x/7)

La gráfica requiere la evaluación las funciones, que por simplicidad de evaluación, su formas simbólicas se convierten a su forma ‘lambda’.

Con la gráfica se verifica que la raiz de dp(x)/dx (en naranja) pasa por el máximo y mínimo de p(x) (en azul).

que se obtienen con las siguientes instrucciones en python:

# 1ra Evaluación I Término 2010
# tema 2. encendido tv
# Tarea: aplicar el método de Newton-Raphson
# solo se muestra la función y sus derivadas 1 y 2
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt

# función bajo análisis en forma simbólica
x = sp.Symbol('x')
pxs = (1/2.5)*(-10*sp.sin(12*x/7)*sp.exp(-24*x/7) + (48*x/7)*sp.exp(-8*x/7)+0.8)

# derivadas
dpxs = pxs.diff(x,1)
d2pxs = pxs.diff(x,2)

# SALIDA
print('primera derivada: ')
print(dpxs)
print('segunda derivada: ')
print(d2pxs)

# conversion a lambda
pxn = sp.utilities.lambdify(x,pxs, 'numpy')
dpxn = sp.utilities.lambdify(x,dpxs, 'numpy')
d2pxn = sp.utilities.lambdify(x,d2pxs, 'numpy')

# observar gráfica
a = 0
b = 4
muestras
tolera = 0.0001

xi = np.linspace(a,b, muestras)
pxi = pxn(xi)
dpxi = dpxn(xi)
d2pxi = d2pxn(xi)

# Gráfica
plt.plot(xi,pxi, label = 'pxi')
plt.plot(xi,dpxi, label = 'dpxi')
plt.plot(xi,d2pxi, label = 'd2pxi')
plt.axhline(0)
plt.legend()
plt.show()

# Tarea: encontrar la raiz de dpxn
# usando el método de Newton-Raphson

Ejercicio: 1Eva_IT2010_T1_MN Demanda y producción sin,log

Desarrollo Analítico

Para la demanda, el intervalo de existencia es [0,3]

demanda(t) = sin(t)

Para la oferta, el intervalo de existencia inicia en 1, limitado por la demanda [1,3]

oferta(t) = ln(t)

la oferta satisface la demanda cuando ambas son iguales

demanda(t) = oferta(t) sin(t) = ln(t)

por lo que el tiempo t se encuentra con algun método para determinar la raiz de:

sin(t) - ln(t) = 0 f(t) = sin(t) - ln(t)

Observe que las curvas de oferta y demanda se intersectan en el mismo punto en el eje x que la función f(t).

Use un método para encontrar el valor t que satisface la ecuación.

---

Algoritmo en Python

instrucciones para la gráfica, no para el algoritmo de búsqueda de raiz que es tarea.

# 1Eva_IT2010_T1_MN Demanda y producción sin,log
# Solo para analizar el problema
# Tarea: Añadir algoritmo de buscar raiz.
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
# demanda
ad = 0
bd = 3
muestrasd = 31
# oferta
ao = 1
bo = 3
muestras0  = 21

demanda = lambda t: np.sin(t)
oferta = lambda t: np.log(t)
f = lambda t: demanda(t)-oferta(t)

# PROCEDIMIENTO
tid = np.linspace(ad,bd,muestrasd)
demandai = demanda(tid)

tio = np.linspace(ao,bo,muestras0)
ofertai = oferta(tio)

fi = f(tio)

# SALIDA
plt.plot(tid,demandai, label='demanda')
plt.plot(tio,ofertai, label ='oferta')
plt.plot(tio,fi,label='f(t)= demanda-oferta')
plt.axhline(0,color='black')
plt.axvline(2.2185, color = 'magenta')
plt.xlabel('tiempo')
plt.ylabel('unidades')
plt.legend()
plt.grid()
plt.show()

Ejercicio: 3Eva_IT2009_T3 Integrar Simpson compuesta

La fórmula a integrar es:

\int_0^1 \frac{\cos (2x)}{x^{1/3}} \delta x

Que tiene la forma:

da como resultado:

el área bajo la curva es:  0.879822622256

Algoritmo en Python

# 3Eva_IT2009_T3 Integrar Simpson compuesta
import numpy as np
import matplotlib.pyplot as plt

funcionx = lambda x: np.cos(2*x)/(x**(1/3))

# INGRESO
a = 0.00001
b = 1
tramos = 10000

# PROCEDIMIENTO
h = (b-a)/tramos
x = a
area = 0
for i in range(0,tramos,2):
    deltaA = (h/3)*(funcionx(x)+4*funcionx(x+h)+funcionx(x+2*h))
    area = area + deltaA
    x = x + 2*h
    
# para la gráfica
xi = np.linspace(a,b,tramos+1)
fxi = funcionx(xi)

print('el área bajo la curva es: ', area)

# Gráfica
plt.plot(xi,fxi)
plt.title('Funcion a integrar')
plt.grid()
plt.xlabel('x')
plt.show()

Tarea: convertir a función el cálculo de Simpson

Ejercicio: 1Eva_IT2009_T2 Materiales y Productos 3×4

1. Plantear el sistema de ecuaciones

0.2 x0 + 0.5 x1 + 0.4 x2 + 0.2 x3 = 10
0.3 x0 +  0  x1 + 0.5 x2 + 0.6 x3 = 12
0.4 x0 + 0.5 x1 + 0.1 x2 + 0.2 x3 = 15

Observe que hay más incógnitas que ecuaciones.

Para equiparar las ecuaciones con el número de incógnitas, podriamos suponer que uno de los productos NO se fabricará. por ejempo el producto x₃ que podría hacerse igual a cero. Supone que la variable libre es x₃ .

Para mantener la forma de las ecuaciones para otros valores de x₃, se pasa la variable y su coeficiente a la derecha.

0.2 x0 + 0.5 x1 + 0.4 x2 = 10 - 0.2 x3 
0.3 x0 +  0  x1 + 0.5 x2 = 12 - 0.6 x3 
0.4 x0 + 0.5 x1 + 0.1 x2 = 15 - 0.2 x3 

Para analizar el ejercicio, se supondrá que el valor de x₃ = 0, lo que permite usar el modelo del problema como A.X=B .En caso de que x₃ sea diferente de cero,  el vector B modifica, y se puede proceder con el sistema de ecuaciones.

2. Convertir a la forma matricial AX = B

Siendo así, suponiendo que x₃ = 0, el ejercicio se puede desarrollar usando:

A = np.array([[0.2, 0.5, 0.4],
              [0.3, 0.0, 0.5],
              [0.4, 0.5, 0.1]])
B = np.array([[10],
              [12],
              [15]])

que luego armar el algoritmo y su ejecución, obtendría una solución semejante:

array([[ 32.10526316],
       [  3.36842105],
       [  4.73684211]])

Nota: Para desarrollar, se recomienda seguir los pasos indicados en:

http://blog.espol.edu.ec/analisisnumerico/unidad-03-y-04-sistema-de-ecuaciones-pasos/

Encontrada la solución, modifique el algoritmo para calcular B en función de x₃, pregunte el valor al inicio, y vuelva a calcular.

x3 = float(input('cantidad a producir de cuarto producto: ')

Observe el rango para x₃, por ejemplo que debe ser mayor o igual que cero, pues no hay producción negativa. De producir solamente ése un producto, el valor máximo de unidades a obtener no superaría lo posible con la cantidad de materiales disponible.

Ejemplo:

x3 = 1
B3 = np.array([[0.2],
	       [0.6],
	       [0.2]])
Bnuevo = B - x3*B3

>>> Bnuevo
array([[  9.8],
       [ 11.4],
       [ 14.8]])

Y se vuelve a generar el sistema A.X=Bnuevo

Observación: Algunos productos se fabrican por unidades, no necesesariamente por peso o volumen. ¿comentarios al respecto?

 

Ejercicio: 1Eva_IT2009_T1 Demanda de producto

Desarrollo analítico

– igualar la ecuación al valor buscado, 80

200 t e^{-0.75t} = 80

– forma estándar de la ecuación para el método f(x) = 0:

f(t) = 200 t e^{-0.75t} - 80

– derivada de la ecuación

f'(t) = 200 e^{-0.75t} + 200 t (-0.75) e^{-0.75t} f'(t) = 200 e^{-0.75t}(1-0.75t)

– fórmula del método de Newton-Raphson

t_{i+1} = t_i - \frac{f(t)}{f'(t)}

– Punto inicial. Como la variable es t, tiempo, el rango de análisis es t>0
El valor inicial de búsqueda se selecciona t₀ = 1

iteración 1:

t_{1} = 1 - \frac{200 (1) e^{-0.75(1)} - 80}{200 e^{-0.75(1)}(1-0.75(1))}

error = 0.6128

iteración 2:

t_{2} = 0.3872 - \frac{200 (0.3872) e^{-0.75(0.3872)} - 80}{200 e^{-0.75(0.3872)}(1-0.75(0.3872))}

error = 0.208

iteracion 3:

t_{3} = 0.5952 - \frac{200 (0.5952) e^{-0.75(0.5952)} - 80}{200 e^{-0.75(0.5952)}(1-0.75(0.5952))}

error = 5.3972e-02
…
tabla de iteraciones

[  xi,       xnuevo,   f(xi),   f'(xi),    tramo]
[  1.        0.3872   14.4733   23.6183   0.6128]
[  0.3872    0.5952  -22.0776  106.1511   0.208 ]
[  5.9518e-01   6.4916e-01  -3.8242e+00   7.0855e+01   5.3972e-02]
[  6.4916e-01   6.5252e-01  -2.1246e-01   6.3069e+01   3.3686e-03]
[  6.5252e-01   6.5254e-01  -7.9031e-04   6.2600e+01   1.2625e-05]
raiz:  0.65253630273

Se obtiene el valor de la raíz con 5 iteraciones, y un error de 1.2625e-05

---

Desarrollo con Python

Tarea: desarrollar el literal b

Ejercicio: 1Eva_IIT2008_T3_MN Ganancia en inversión

Se usan para cada par ordenado, punto, la evaluación del polinomio para generar las ecuaciones:

[[3.2, 5.12],
 [3.8, 6.42],
 [4.2, 7.25],
 [4.5, 6.85]]

modelo propuesto:

f(x) = a_1 x^3 + a_2 x^2 + a_3 x + a_4

usando los datos

a_1 (3.2)^3 + a_2 (3.2)^2 + a_3 (3.2) + a_4 = 5.12 a_1 (3.8)^3 + a_2 (3.8)^2 + a_3 (3.8) + a_4 = 6.42 a_1 (4.2)^3 + a_2 (4.2)^2 + a_3 (4.2) + a_4 = 7.25 a_1 (4.5)^3 + a_2 (4.5)^2 + a_3 (4.5) + a_4 = 6.85

Se convierte a la forma Ax=B
\begin{bmatrix} (3.2)^3 && (3.2)^2 && (3.2) && 1 \\ (3.8)^3 && (3.8)^2 && (3.8) && 1 \\ (4.2)^3 && (4.2)^2 && (4.2) && 1 \\ (4.5)^3 && (4.5)^2 && (4.5) && 1 \end{bmatrix} . \begin{bmatrix} a_1 \\ a_2 \\ a_3 \\ a_4 \end{bmatrix} = \begin{bmatrix} 5.12 \\ 6.42 \\ 7.25 \\6.85 \end{bmatrix}

Se crea la matriz aumentada

\begin{bmatrix} (3.2)^3 && (3.2)^2 && (3.2) && 1 && 5.12\\ (3.8)^3 && (3.8)^2 && (3.8) && 1 && 6.42 \\ (4.2)^3 && (4.2)^2 && (4.2) && 1 && 7.25 \\ (4.5)^3 && (4.5)^2 && (4.5) && 1 && 6.85 \end{bmatrix}

Se pivotea por filas:

\begin{bmatrix} (4.5)^3 && (4.5)^2 && (4.5) && 1 && 6.85 \\ (4.2)^3 && (4.2)^2 && (4.2) && 1 && 7.25 \\ (3.8)^3 && (3.8)^2 && (3.8) && 1 && 6.42 \\ (3.2)^3 && (3.2)^2 && (3.2) && 1 && 5.12 \end{bmatrix}

Como se pide un método directo, se inicia con el algoritmo de eliminación hacia adelante

\begin{bmatrix} (4.5)^3 && (4.5)^2 && (4.5) \\ (4.2)^3 - (4.5)^3\frac{(4.2)^3}{(4.5)^3} && (4.2)^2 - (4.5)^2\frac{(4.2)^3}{(4.5)^3} && (4.2) - (4.5)\frac{(4.2)^3}{(4.5)^3} \\ (3.8)^3 - (4.5)^3\frac{(3.8)^3}{(4.5)^3} && (3.8)^2 - (4.5)^2\frac{(3.8)^3}{(4.5)^3} && (3.8) -(4.5)\frac{(3.8)^3}{(4.5)^3} \\ (3.2)^3 - (4.5)^3\frac{(3.2)^3}{(4.5)^3} && (3.2)^2 -(4.5)^2\frac{(3.2)^3}{(4.5)^3} && (3.2) - (4.5)\frac{(3.2)^3}{(4.5)^3} \end{bmatrix}

continua a la derecha de la matriz:

\begin{bmatrix} 1 && 6.85 \\ 1 - 1\frac{(4.2)^3}{(4.5)^3} && 7.25 - 6.85\frac{(4.2)^3}{(4.5)^3} \\ 1 -1\frac{(3.8)^3}{(4.5)^3} && 6.42 - 6.85\frac{(3.8)^3}{(4.5)^3}\\1 -1\frac{(3.2)^3}{(4.5)^3} && 5.12-6.85\frac{(3.2)^3}{(4.5)^3} \end{bmatrix}

[[91.125  20.25   4.5    1.     6.85 ]
 [ 0.      1.176  0.541  0.186  1.680]
 [ 0.      2.246  1.090  0.397  2.295]
 [ 0.      2.958  1.581  0.640  2.656]]
Elimina hacia adelante
[[91.125  20.250  4.500  1.000  6.850]
 [ 0.      1.176  0.541  0.186  1.680]
 [ 0.      0.     0.056  0.040 -0.915]
 [ 0.      0.     0.220  0.170 -1.571]]
Elimina hacia adelante
[[91.125  20.250  4.500  1.000  6.850]
 [ 0.      1.176  0.541  0.186  1.680]
 [ 0.      0.000  0.056  0.040 -0.915]
 [ 0.      0.000  0.000  0.010  2.006]]
Elimina hacia adelante
[[91.125  20.250  4.500  1.000  6.850]
 [ 0.      1.176  0.541  0.186  1.680]
 [ 0.      0.     0.056  0.040 -0.915]
 [ 0.      0.     0.     0.010  2.006]]
Elimina hacia atras
[[1. 0. 0. 0.   -3.67490842]
 [0. 1. 0. 0.   41.06730769]
 [0. 0. 1. 0. -149.92086081]
 [0. 0. 0. 1.  184.75692308]]
el vector solución X es:
[[  -3.67490842]
 [  41.06730769]
 [-149.92086081]
 [ 184.75692308]]

verificar que A.X = B
[[6.85]
 [7.25]
 [6.42]
 [5.12]]

con lo que el polinomio buscado es:

f(x) = -3.67490842 x^3 + 41.06730769 x^2 + -149.92086081 x + 184.75692308

que genera la siguiente gráfica:

para encontrar la cantidad necesaria a invertir y obtener 6.0 de ganancia en f(x):

6.0 = -3.67490842 x^3 + 41.06730769 x^2 + -149.92086081 x + 184.75692308

que para usar en el algoritmo se realiza se reordena como g(x) = 0

-3.67490842 x^3 + 41.06730769 x^2 +

-149.92086081 x + 184.75692308 - 6.0 = 0
y se aplica la búsqueda de raices en el rango [a, b] que de la gráfica se estima en [3.2, 3.8]

La ejecución del algoritmo de búsqueda queda como tarea.

---

Algoritmo en python para obtener la gráfica y respuesta a la matriz:

# Método de Gauss-Jordan ,
# Recibe las matrices A,B
# presenta solucion X que cumple: A.X=B
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
puntos = np.array([[3.2, 5.12],
                   [3.8, 6.42],
                   [4.2, 7.25],
                   [4.5, 6.85]])

A = np.array([[4.5**3 , 4.5**2 , 4.5 , 1],
              [4.2**3 , 4.2**2 , 4.2 , 1],
              [3.8**3 , 3.8**2 , 3.8 , 1],
              [3.2**3 , 3.2**2 , 3.2, 1]])

B = np.array([[6.85],
              [7.25],
              [6.42],
              [5.12]])

# PROCEDIMIENTO
casicero = 1e-15 # 0
AB = np.concatenate((A,B),axis=1)
tamano = np.shape(AB)
n = tamano[0]
m = tamano[1]

print('matriz aumentada: ')
print(AB)
# Gauss elimina hacia adelante
# tarea: verificar términos cero
for i in range(0,n,1):
    pivote = AB[i,i]
    adelante = i+1 
    for k in range(adelante,n,1):
        if (np.abs(pivote)>=casicero):
            factor = AB[k,i]/pivote
            AB[k,:] = AB[k,:] - factor*AB[i,:]
    print('Elimina hacia adelante')
    print(AB)

# Gauss-Jordan elimina hacia atras
ultfila = n-1
ultcolumna = m-1
for i in range(ultfila,0-1,-1):
    # Normaliza a 1 elemento diagonal
    AB[i,:] = AB[i,:]/AB[i,i]
    pivote = AB[i,i] # uno
    # arriba de la fila i
    atras = i-1 
    for k in range(atras,0-1,-1):
        if (np.abs(AB[k,i])>=casicero):
            factor = pivote/AB[k,i]
            AB[k,:] = AB[k,:]*factor - AB[i,:]
        else:
            factor= 'division para cero'
print('Elimina hacia atras')
print(AB)

X = AB[:,ultcolumna]

# Verifica resultado
verifica = np.dot(A,X)

# SALIDA
print('el vector solución X es:')
print(np.transpose([X]))

print('verificar que A.X = B')
print(np.transpose([verifica]))

# Revisa polinomio
a = np.min(puntos[:,0])
b = np.max(puntos[:,0])
muestras = 51

px = lambda x: X[0]*x**3 + X[1]*x**2 +X[2]*x + X[3]
xi = np.linspace(a,b,muestras)
pxi = px(xi)

# gráfica
plt.plot(xi,pxi)
plt.plot(puntos[:,0],puntos[:,1],'ro')
plt.show()

Ejercicio: 1Eva_IIT2008_T1 Distribuidores de productos

Siguiendo las instrucciones del enunciado, el promedio de precios del nodo A, se conforma de los precios en los nodos aledaños menos el costo de transporte.

precio en X₁ para A = precio en nodo_A – costo de transporte_A

siguiendo el mismo procedimiento,

precio en X₁ para A: (3.1-0.2)
precio de X₁ para B: (2.8-0.3)
precio de X₁ para C: (2.7-0.4)
precio de X₁ para X₂: (X₂-0.1)
precio de X₁ para X₃: (X₃-0.5)

x_1 = \frac{1}{5} \Big[ (3.1-0.2)+(2.8-0.3)+(2.7-0.4)+ +(x_2-0.1)+(x_3-0.5)\Big] x_1 = \frac{1}{5} \Big[ 2.9+2.5 +2.3+x_2+x_3-0.6\Big] x_1 = \frac{1}{5} (7.1+x_2+x_3) 5x_1 = 7.1+x_2+x_3 5x_1-x_2-x_3 = 7.1

Se continua con el mismo proceso para los siguientes nodos:

x_2 = \frac{1}{4} \Big[ (3.2-0.5)+(3.4-0.3) +(x_1-0.1)+(x_3-0.2)\Big] 4x_2 = (3.2-0.5)+(3.4-0.3) +(x_1-0.1)+(x_3-0.2) 4x_2 = 2.7+3.1 +x_1+x_3-0.3 -x_1+4x_2-x_3 = 5.5

Para X₃

x_3 = \frac{1}{4} \Big[ (3.3-0.3)+(2.9-0.2) +(x_1-0.5)+(x_2-0.2)\Big] 4x_3 = 3.0+2.7+x_1+x_2-0.7 4x_3 = 5+x_1+x_2 -x_1-x_2+4x_3= 5

El sistema de ecuaciones se convierte en:

\begin{cases} 5x_1-x_2-x_3 = 7.1 \\ -x_1+4x_2-x_3 = 5.5 \\-x_1-x_2+4x_3= 5 \end{cases}

Para resolve se convierte a la forma Ax=B

\begin{bmatrix} 5 && -1 && -1 \\ -1 && 4 && -1 \\ -1 && -1 && 4 \end{bmatrix} . \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 7.1 \\ 5.5 \\5 \end{bmatrix}

En los métodos directos se usa la forma de matriz aumentada

\begin{bmatrix} 5 && -1 && -1 && 7.1 \\ -1 && 4 && -1 && 5.5 \\ -1 && -1 && 4 && 5 \end{bmatrix}

pivoteo: no es necesario, pues la matriz ya está ordenada de forma diagonalmente dominante.

Eliminación hacia adelante
1ra Iteración

\begin{bmatrix} 5 && -1 && -1 && 7.1 \\ -1-5\big(\frac{-1}{5}\big) && 4 -(-1)\big(\frac{-1}{5}\big) && -1 -(-1)\big(\frac{-1}{5}\big) && 5.5-7.1\big(\frac{-1}{5}\big) \\ -1-5\big(\frac{-1}{5}\big) && -1-(-1)1\big(\frac{-1}{5}\big) && 4-(-1)\big(\frac{-1}{5}\big) && 5-7.1\big(\frac{-1}{5}\big) \end{bmatrix} \begin{bmatrix} 5 && -1 && -1 && 7.1 \\ 0 && 3.8 && -1.2 && 6.92 \\ 0 && -1.2 && 3.8 && 6.42 \end{bmatrix}

Eliminación hacia adelante
2da Iteración

Elimina hacia adelante
[[ 5.         -1.         -1.          7.1       ]
 [ 0.          3.8        -1.2         6.92      ]
 [ 0.          0.          3.42105263  8.60526316]]

Eliminación hacia atras, continuando el desarrollo de forma semejante a los pasos anteriores se obtiene:

Elimina hacia atras
[[ 1.         -0.         -0.          2.44615385]
 [ 0.          1.         -0.          2.61538462]
 [ 0.          0.          1.          2.51538462]]
el vector solución X es:
[[2.44615385]
 [2.61538462]
 [2.51538462]]
verificar que A.X = B
[[7.1]
 [5.5]
 [5. ]]

---

Para el literal b se usa como referencia el número de condición:

>>> np.linalg.cond(A)
2.5274158815808474

El número de condición es cercano a 1, dado que la matriz A es diagonalmente dominante pues los valores mayores de la fila se encuentran en la diagonal. Como el número de condición es cercano a 1 el sistema converge usando métodos iterativos.

La selección del vector inicial para las iteraciones siguiendo el enunciado del problema, se evita el vector cero dado que el precio de un producto para una fabrica no puede ser cero. Se observa los valores de los precios, y se encuentra que el rango de existencia en los nodos es [ 2.7, 3.4] que restando el valor de transporte podrían ser un valor menor a 2.7. Por lo que un buen vector inicial será [2,2,2]

Queda como tarea las iteraciones por un método Jacobi.