Ejercicio: 1Eva_2023PAOI_T1 Desacople de cohete de dos etapas
literal a. Planteamiento
La ecuación a usar según el enunciado es y usando los valores dados es:
v = u \ln\Big(\frac{m_0}{m_0-qt}\Big) - gt 800 = 1870 \ln\Big(\frac{195000}{195000-2500 t}\Big) - 9.8 tcon lo que la función para buscar la raíz es:
f(t) = 1870 \ln\Big(\frac{195000}{195000-2500 t}\Big) - 9.8 t -800Literal b. Intervalo de búsqueda
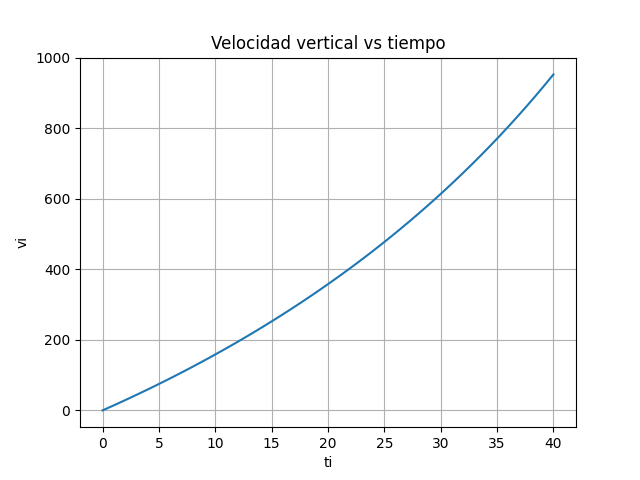
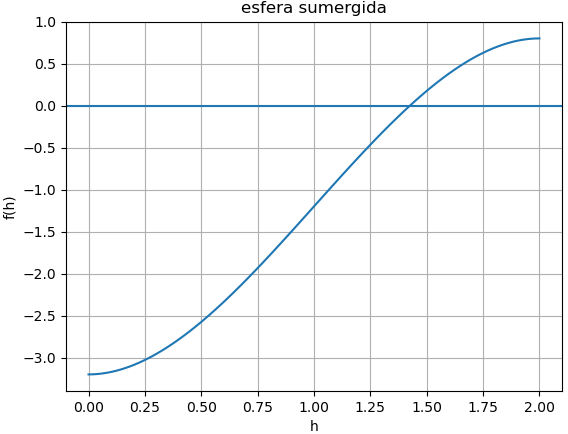
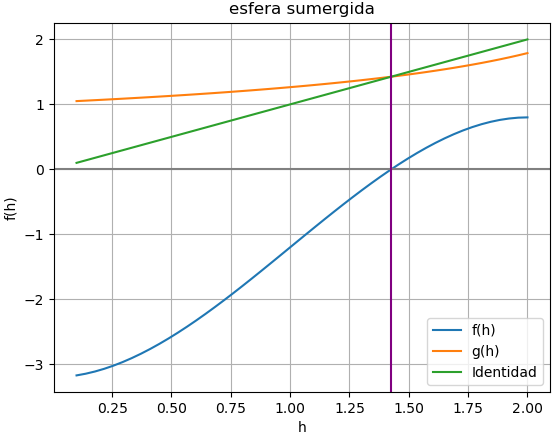
Para el intervalo de búsqueda se puede usar una gráfica e interpretar el punto a buscar alrededor de 800 m/s. Que de la gráfica se observa que un intervalo alrededor de 35 sería válido para el método de la Bisección. Para otros métodos abiertos, también es posible deducir un punto t0.
La validación se muestra con la primera iteración al evaluar f(30) que es negativo y f(40) que es de signo positivo.
# 1Eva_2023PAOI_T1 Desacople de cohete de dos etapas import numpy as np import matplotlib.pyplot as plt # INGRESO v = lambda t: 1870*np.log(195000/(195000-2500*t))-9.8*t a = 0 b = 40 tramos = 51 # PROCEDIMIENTO ti = np.linspace(a,b,tramos) vi = v(ti) # SALIDA plt.plot(ti,vi) plt.xlabel('ti') plt.ylabel('vi') plt.title('Velocidad vertical vs tiempo') plt.grid() plt.show()
literal c. Desarrollo con algoritmo de Bisección
itera =0, intervalo [30,40]
f(30) = 1870 \ln\Big(\frac{195000}{195000-2500 (30)}\Big) - 9.8 (30) -800 = -186.100 f(40) = 1870 \ln\Big(\frac{195000}{195000-2500 (40)}\Big) - 9.8 (40) -800 = 152.759 c= \frac{a+b}{2}= \frac{30+40}{2} = 35 f(35) = 1870 \ln\Big(\frac{195000}{195000-2500 (35)}\Big) - 9.8 (35) -800 = -29.399error = tramo = |40-30| = 10
como f(a) y f(c) son del mismo signo, el intervalo nuevo será [35,40]
itera =1 , intervalo [35,40]
c= \frac{35+40}{2} = 37.5 f(37.5) = 1870 \ln\Big(\frac{195000}{195000-2500 (37.5)}\Big) - 9.8 (37.5) -800 = 58.111error = tramo = |40-35| = 5
como f(c) y f(b) son del mismo signo, el intervalo nuevo será [35,37.5]
itera =2 , intervalo [35,37.5]
c= \frac{37.5+35}{2} = 36.25 f(36.25) = 1870 \ln\Big(\frac{195000}{195000-2500 (36.25)}\Big) - 9.8 (36.25) -800 = 13.518error = tramo = |37.5-35| = 2.5
como f(c) y f(b) son del mismo signo, el intervalo nuevo será [35,36.25]
[ i, a, c, b, f(a), f(c), f(b), tramo] 1 30.000 35.000 40.000 -186.100 -29.399 152.759 10.000 2 35.000 37.500 40.000 -29.399 58.111 152.759 5.000 3 35.000 36.250 37.500 -29.399 13.518 58.111 2.500 4 35.000 35.625 36.250 -29.399 -8.144 13.518 1.250 5 35.625 35.938 36.250 -8.144 2.635 13.518 0.625 6 35.625 35.781 35.938 -8.144 -2.767 2.635 0.312 7 35.781 35.859 35.938 -2.767 -0.069 2.635 0.156 8 35.859 35.898 35.938 -0.069 1.282 2.635 0.078 raiz: 35.8984375 >>>
literal d. tolerancia y errores
La tolerancia depende de la escala a la que se mide y el instrumento de medición. Si consideramos décimas de segundo la tolerancia será de 10-1. ó 0.1
Los errores entre iteraciones se muestran en el literal anterior.
literal e. convergencia
Los errores en cada iteración disminuye, lo que muestra que el método converge. Luego de 8 iteraciones se encuentra el tiempo ti a usar como 35.8 s.
Se adjunta el algoritmo de la bisección ajustado para el ejercicio. La gráfica es complementaria a la presentada en el literal b, que puede ser incorporada al mismo algoritmo para la presentación.
Instrucciones en Python
# Algoritmo de Bisección # 1Eva_2023PAOI_T1 Desacople de cohete de dos etapas import numpy as np # INGRESO fx = lambda t: 1870*np.log(195000/(195000-2500*t))-9.8*t -800 a = 30 b = 40 tolera = 0.1 # PROCEDIMIENTO tabla = [] tramo = b-a fa = fx(a) fb = fx(b) i = 1 while (tramo>tolera): c = (a+b)/2 fc = fx(c) tabla.append([i,a,c,b,fa,fc,fb,tramo]) i = i + 1 cambia = np.sign(fa)*np.sign(fc) if (cambia<0): b = c fb = fc else: a=c fa = fc tramo = b-a c = (a+b)/2 fc = fx(c) tabla.append([i,a,c,b,fa,fc,fb,tramo]) tabla = np.array(tabla) raiz = c # SALIDA np.set_printoptions(precision = 4) print('[ i, a, c, b, f(a), f(c), f(b), tramo]') # print(tabla) # Tabla con formato n=len(tabla) for i in range(0,n,1): unafila = tabla[i] formato = '{:.0f}'+' '+(len(unafila)-1)*'{:.3f} ' unafila = formato.format(*unafila) print(unafila) print('raiz: ',raiz)