Referencia: Sympy ODE solver. Stewart James. Cálculo de varias variables. 17.2 p1148 pdf545. Lathi Ejemplo 2.1.a p155, Ejemplo 2.9 p175, Oppenheim 2.4.1 p117, ejemplo 1 de Modelo entrada-salida,
Continuando con el ejercicio de la sección anterior de una ecuación diferencial ordinaria, lineal y de coeficientes constantes, se obtuvo la solución homogénea o ecuación complementaria con dsolve(). Para el desarrollo analítico de la solución se requieren describir los pasos tales como la ecuación auxiliar, como se describe a continuación como un ejercicio de análisis de expresiones con Sympy.
Ejemplo 1. Ecuación diferencial de un circuito RLC, ecuación complementaria.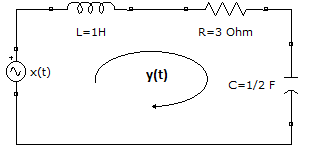
El circuito RLC con entrada x(t) de la figura tiene una corriente y(t) o salida del sistema que se representa por medio de una ecuación diferencial.
\frac{d^{2}y(t)}{dt^{2}} + 3\frac{dy(t)}{dt} + 2y(t) = \frac{dx(t)}{dt}Las condiciones iniciales del sistema a tiempo t=0 son y(0)=0 , y'(0)=-5
1. Ecuación diferencial y condiciones de frontera o iniciales
La ecuación diferencial del ejercicio con Sympy se escribe con el operador sym.diff(y,t,1). Indicando la variable independiente ‘t‘, que ‘y‘ es una función y el orden de la derivada con 1. esquema que se mantiene para la descripción de las condiciones iniciales.
# ecuacion: lado izquierdo = lado derecho # Left Hand Side = Right Hand Side LHS = sym.diff(y(t),t,2) + 3*sym.diff(y(t),t,1) + 2*y(t) RHS = sym.diff(x(t),t,1) ecuacion = sym.Eq(LHS,RHS) # condiciones de frontera o iniciales y_cond = {y(0) : 0, sym.diff(y(t),t,1).subs(t,0) : -5}
2. Clasificar la ecuación diferencial ordinaria
Sympy permite revisar el tipo de EDO a resolver usando la instrucción:
>>> sym.classify_ode(ecuacion, y(t)) ('factorable', 'nth_linear_constant_coeff_variation_of_parameters', 'nth_linear_constant_coeff_variation_of_parameters_Integral') >>>
3. Ecuación homogenea
Para el análisis de la respuesta del circuito, se inicia haciendo la entrada x(t)=0, también conocida como ecuación para «respuesta a entrada cero» o ecuación homogenea.
En el algoritmo, La ecuación homogénea se obtiene al substituir x(t)=0 en cada lado de la ecuación, que también es un paso para encontrar la respuesta a entrada cero. La ecuacion homogenea se escribe de la forma f(t)=0.
# ecuación homogénea x(t)=0, entrada cero
RHSx0 = ecuacion.rhs.subs(x(t),0).doit()
LHSx0 = ecuacion.lhs.subs(x(t),0).doit()
homogenea = LHSx0 - RHSx0
4. Ecuación auxiliar o característica.
En la ecuación homogenea , se procede a sustituir en la ecuación el operador dy/dt de la derivada con una variable r elevada al orden de la derivada de cada término . El resultado es una ecuación algebraica que se analiza encontrando las raíces de r.
r ^2 + 3r +2 = 0Los valores de ‘r’ que resuelven la ecuación permiten estimar la forma de la solución para y(t) conocida como la ecuación general
Se usan diferentes formas para mostrar la ecuación auxiliar, pues en algunos casos se requiere usar la forma de factores, en otros casos los valores de las raíces y las veces que se producen. Formas usadas para generar diagramas de polos y ceros, o expresiones de transformada de Laplace. Motivo por el que los resultados se los presenta en un diccionario, y asi usar la respuesta que sea de interés en cada caso.
homogenea :
2
d d
2*y(t) + 3*--(y(t)) + ---(y(t)) = 0
dt 2
dt
auxiliar : r**2 + 3*r + 2
Q : r**2 + 3*r + 2
Q_factor : (r + 1)*(r + 2)
Q_raiz : {-1: 1, -2: 1}
>>>
Instrucciones con Python
# Ecuación Diferencial Ordinaria EDO # ecuación auxiliar o característica # Lathi 2.1.a pdf 155, (D^2+ 3D + 2)y = Dx import sympy as sym # INGRESO t = sym.Symbol('t', real=True) r = sym.Symbol('r') y = sym.Function('y') x = sym.Function('x') # ecuacion: lado izquierdo = lado derecho # Left Hand Side = Right Hand Side LHS = sym.diff(y(t),t,2) + 3*sym.diff(y(t),t,1) + 2*y(t) RHS = sym.diff(x(t),t,1) ecuacion = sym.Eq(LHS,RHS) # condiciones de frontera o iniciales y_cond = {y(0) : 0, sym.diff(y(t),t,1).subs(t,0) : -5} # PROCEDIMIENTO def edo_lineal_auxiliar(ecuacion, t = sym.Symbol('t'),r = sym.Symbol('r'), y = sym.Function('y'),x = sym.Function('x')): ''' ecuacion auxiliar o caracteristica de EDO t independiente ''' # ecuación homogénea x(t)=0, entrada cero RHSx0 = ecuacion.rhs.subs(x(t),0).doit() LHSx0 = ecuacion.lhs.subs(x(t),0).doit() homogenea = LHSx0 - RHSx0 homogenea = sym.expand(homogenea,t) # ecuación auxiliar o característica Q = 0*r term_suma = sym.Add.make_args(homogenea) for term_k in term_suma: orden_k = sym.ode_order(term_k,y) coef = 1 # coefientes del término suma factor_mul = sym.Mul.make_args(term_k) for factor_k in factor_mul: cond = factor_k.has(sym.Derivative) cond = cond or factor_k.has(y(t)) if not(cond): coef = coef*factor_k Q = Q + coef*(r**orden_k) # Q factores y raices Q_factor = sym.factor(Q,r) Q_poly = sym.poly(Q,r) Q_raiz = sym.roots(Q_poly) auxiliar = {'homogenea' : sym.Eq(homogenea,0), 'auxiliar' : Q, 'Q' : Q, 'Q_factor' : Q_factor, 'Q_raiz' : Q_raiz } return(auxiliar) # analiza la ecuación diferencial edo_tipo = sym.classify_ode(ecuacion, y(t)) auxiliar = edo_lineal_auxiliar(ecuacion,t,r) # SALIDA print('clasifica EDO:') for untipo in edo_tipo: print(' ',untipo) print('ecuacion auxiliar:') for entrada in auxiliar: print(' ',entrada,':',auxiliar[entrada])
Otra forma de mostrar el resultado es usando un procedimiento creado para mostrar elementos del diccionario según corresponda a cada tipo. el procedimiento se adjunta al final.
Las funciones se incorporan a los algoritmos del curso en matg1052.py
6. Ecuación diferencial, ecuación general y complementaria con Sympy-Python
La ecuación general se encuentra con la instrucción sym.dsolve(), sin condiciones iniciales, por que el resultado presenta constantes Ci por determinar.
# solucion general de ecuación homogénea
general = sym.dsolve(homogenea, y(t))
general = general.expand()
el resultado para el ejercicio es
general :
-t -2*t
y(t) = C1*e + C2*e
Para encontrar los valores de las constantes, se aplica cada una de las condiciones iniciales a la ecuación general, obteniendo un sistema de ecuaciones.
# Aplica condiciones iniciales o de frontera eq_condicion = [] for cond_k in y_cond: # cada condición valor_k = y_cond[cond_k] orden_k = sym.ode_order(cond_k,y) if orden_k==0: # condicion frontera t_k = cond_k.args[0] # f(t_k) expr_k = general.rhs.subs(t,t_k) else: # orden_k>0 # f.diff(t,orden_k).subs(t,t_k) subs_param = cond_k.args[2] # en valores t_k = subs_param.args[0] # primer valor dyk = general.rhs.diff(t,orden_k) expr_k = dyk.subs(t,t_k) eq_condicion.append(sym.Eq(valor_k,expr_k))
con el siguiente resultado:
eq_condicion : 0 = C1 + C2 -5 = -C1 - 2*C2
El sistema de ecuaciones se resuelve con la instrucción
constante = sym.solve(eq_condicion)
que entrega un diccionario con cada valor de la constante
constante : {C1: -5, C2: 5}
La ecuación complementaria se obtiene al sustituir en la ecuación general los valores de las constantes.
El resultado del algoritmo
homogenea :
2
d d
2*y(t) + 3*--(y(t)) + ---(y(t)) = 0
dt 2
dt
general :
-t -2*t
y(t) = C1*e + C2*e
eq_condicion :
0 = C1 + C2
-5 = -C1 - 2*C2
constante : {C1: -5, C2: 5}
complementaria :
-t -2*t
y(t) = - 5*e + 5*e
>>>
Instrucciones con Python
Las instrucciones detalladas se presentan en el algoritmo integrado.
# Solución complementaria a una Ecuación Diferencial Ordinaria EDO # Lathi 2.1.a pdf 155, (D^2+ 3D + 2)y = Dx import sympy as sym equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] import matg1052 as fcnm # INGRESO t = sym.Symbol('t', real=True) r = sym.Symbol('r') y = sym.Function('y') x = sym.Function('x') # ecuacion: lado izquierdo = lado derecho # Left Hand Side = Right Hand Side LHS = sym.diff(y(t),t,2) + 3*sym.diff(y(t),t,1) + 2*y(t) RHS = sym.diff(x(t),t,1) ecuacion = sym.Eq(LHS,RHS) # condiciones de frontera o iniciales y_cond = {y(0) : 0, sym.diff(y(t),t,1).subs(t,0) : -5} # PROCEDIMIENTO def edo_lineal_complemento(ecuacion,y_cond): # ecuación homogénea x(t)=0, entrada cero RHSx0 = ecuacion.rhs.subs(x(t),0).doit() LHSx0 = ecuacion.lhs.subs(x(t),0).doit() homogenea = LHSx0 - RHSx0 # solucion general de ecuación homogénea general = sym.dsolve(homogenea, y(t)) general = general.expand() # Aplica condiciones iniciales o de frontera eq_condicion = [] for cond_k in y_cond: # cada condición valor_k = y_cond[cond_k] orden_k = sym.ode_order(cond_k,y) if orden_k==0: # condicion frontera t_k = cond_k.args[0] # f(t_k) expr_k = general.rhs.subs(t,t_k) else: # orden_k>0 subs_param = cond_k.args[2] # en valores t_k = subs_param.args[0] # primer valor dyk = sym.diff(general.rhs,t,orden_k) expr_k = dyk.subs(t,t_k) eq_condicion.append(sym.Eq(valor_k,expr_k)) constante = sym.solve(eq_condicion) # ecuacion complementaria # reemplaza las constantes en general yc = general for Ci in constante: yc = yc.subs(Ci, constante[Ci]) complemento = {'homogenea' : sym.Eq(homogenea,0), 'general' : general, 'eq_condicion' : eq_condicion, 'constante' : constante, 'complementaria' : yc} return(complemento) # analiza ecuacion diferencial edo_tipo = sym.classify_ode(ecuacion, y(t)) auxiliar = fcnm.edo_lineal_auxiliar(ecuacion,t,r) complemento = edo_lineal_complemento(ecuacion,y_cond) yc = complemento['complementaria'].rhs # SALIDA print('clasifica EDO:') for elemento in edo_tipo: print(' ',elemento) fcnm.print_resultado_dict(auxiliar) fcnm.print_resultado_dict(complemento)
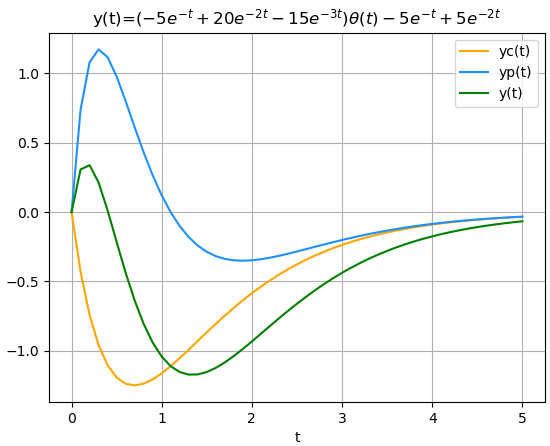
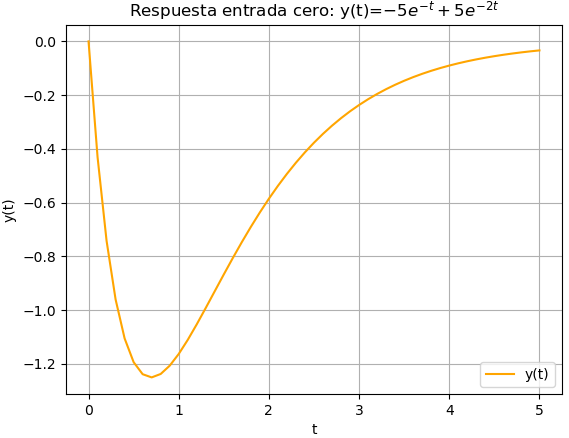
7. Gráfica de la ecuación complementaria yc
Para la gráfica se procede a convertir la ecuación yc en la forma numérica con sym.lambdify(). Se usa un intervalo de tiempo entre [0,5] y 51 muestras con el siguiente resultado:
Instrucciones en Python
# GRAFICA ------------------ import numpy as np import matplotlib.pyplot as plt # INGRESO t_a = 0 ; t_b = 5 # intervalo tiempo [t_a,t_b] muestras = 51 # PROCEDIMIENTO yt = sym.lambdify(t,yc, modules=equivalentes) ti = np.linspace(t_a,t_b,muestras) yi = yt(ti) # Grafica plt.plot(ti,yi, color='orange', label='yc(t)') untitulo = 'yc(t)=$'+ str(sym.latex(yc))+'$' plt.title(untitulo) plt.xlabel('t') plt.ylabel('yc(t)') plt.legend() plt.grid() plt.show()
8. Mostrar el resultado del diccionario según el tipo de entrada
Para mostrar los resultados de una forma más fácil de leer, se usará sym.pprint() para las ecuaciones, y print() simple para los demás elementos del resultado
def print_resultado_dict(resultado): ''' print de diccionario resultado formato de pantalla ''' for entrada in resultado: tipo = type(resultado[entrada]) if tipo == sym.core.relational.Equality: print(entrada,':') sym.pprint(resultado[entrada]) elif tipo==list or tipo==tuple: tipoelem = type(resultado[entrada][0]) if tipoelem==sym.core.relational.Equality: print(entrada,':') for fila in resultado[entrada]: sym.pprint(fila) else: print(entrada,':') for fila in resultado[entrada]: print(' ',fila) else: print(entrada,':',resultado[entrada]) return()