Etiqueta: raíces de ecuaciones

3ra Evaluación 2020-2021 PAO I. 22/Septiembre/2020

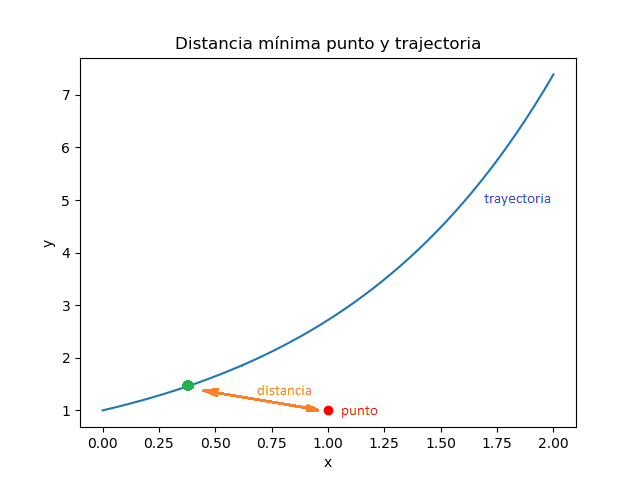
Tema 1. (30 puntos) Calcule el punto de la curva en el plano x-y definida por la función

y = e^{-x} , x ∈ R

que se encuentra más cercano al punto(1, 1).

a. Encuentre un intervalo apropiado para aproximar este valor mediante el método de Newton.

b. Usando este método, elabore una tabla que contenga las columnas de la tabla mostrada:

i	xi	f(xi)	Ei
0
1
2
3

donde f(x) = 0 define el problema a resolver y

E_i = |x_i+1 − x_i|, i≥0.

Use como criterio de parada E_i ≤ 10⁻⁷.
Para los cálculos utilice todos los decimales que muestra la calculadora.

Rúbrica: literal a (5 puntos), planteamiento del método (5 puntos). iteraciones (15 puntos), cálculo de errores (5 puntos)

Referencia: NASA: Cinco asteroides se aproximan a la Tierra; los dos primeros este fin de semana. 11 de Julio, 2020. https://www.eluniverso.com/noticias/2020/07/11/nota/7901811/nasa-asteroides-planeta-tierra

Un asteroide recién descubierto pasará este jueves muy cerca de la Tierra. 23 de septiembre, 2020. https://www.eluniverso.com/noticias/2020/09/23/nota/7987777/asteroide-recien-descubierto-pasara-este-jueves-muy-cerca-tierra

1ra Evaluación II Término 2019-2020. 26/Noviembre/2019. MATG1013

Tema 1. (30 puntos). Considere la sucesión

\Big( x_n \Big)_{n=0}^{+ \infty}

cuya ecuación recursiva es:

x_n = g(x) = \sqrt{3 + x_{n-1}}

para n  ∈ Ν

a) ¿Se puede afirmar que ∀x ∈ [1,3], g(x) ∈ [1,3]?

b) Pruebe que g es una función contractiva en el intervalo [1,3] y estime el valor de la constante de Lipschitz (cota de la derivada de g)

c) Realice 5 iteraciones partiendo del dato inicial x₀ =2, y determine el orden de convergencia.

d) Encuentre el valor teórico de x^* al cual converge la sucesión y estime el error absolito en la iteración 5.

e) Realice 5 iteraciones con el método de bisección en el intervalo [1,3] para aproximar el punto fijo de la función g(x).

Rúbrica: literal a (3 puntos), literal b (3 puntos), literal c (10 puntos), literal d (4 puntos), literal e (10 puntos)

---

Referencia: Burden 9Ed. Definición 10.5 p633, Theorem 2.4 P62;
Contracción https://es.wikipedia.org/wiki/Contracci%C3%B3n_(espacio_m%C3%A9trico).
Función lipschitziana https://es.wikipedia.org/wiki/Funci%C3%B3n_lipschitziana

 

1ra Evaluación I Término 2019-2020. 2/Julio/2019. MATG1013

Tema 2. (30 puntos) Un cable en forma catenaria es aquel que cuelga entre dos puntos que no se encuentran sobre la misma línea vertical. Como se muestra en la figura 1, no está sujeta a más carga que su propio peso. Así, su peso en N/m actúa como una carga uniforme por unidad de longitud a lo largo del cable.

En la figura 2, se ilustra un diagrama de cuerpo libre de una sección AB, donde T_A y T_B son las fuerzas de tensión en el extremo.

Con base en los balances de fuerzas horizontal y vertical, se obtiene para el cable el siguiente modelo:

y = \frac{T_A}{w} cosh \Big( \frac{w}{T_A}x \Big) + y_0 - \frac{T_A}{w}

Donde la altura y del cable está en función de la distancia x.

Además se tiene que:

cosh(z) = \frac{e^z+ e^{-z}}{2}

Utilice el método de Newton-Raphson para hallar el valor del parámetro T_A dado los valores de los parámetros w=12, y₀=6 de modelo que el cable tenga una altura de 15 metros para x=50

Rúbrica: Planteamiento del problema (10 puntos), obtener la derivada (5 puntos), plantear el método (5 puntos), iteraciones (5 puntos), verificar tolerancia (5 puntos)

---

Nota: Todos los temas deben mostrar evidencia del desarrollo del método numérico planteado.

Referencia: Chapra 5Ed Problema 8.17 p219 pdf243. Sears&Zemanski Vol1 12Ed problema 5.63. Cuerda con masa p173. https://es.wikipedia.org/wiki/Catenaria

1ra Evaluación II Término 2018-2019. 10/Noviembre/2018. MATG1013

Tema 4. Para pagar una hipoteca de una casa durante n periodos de tiempo se usa la fórmula:

P = A\Big(\frac{1-(1+i)^{-n}}{i} \Big)

En ésta ecuación, P es el valor presente de la casa, A es el valor del pago periódico de la deuda durante n periodos y la tasa de interés por periodo es i.

Suponga que la casa tiene un valor presente de 70000 dólares y deberá ser pagada mediante 1200 dólares mensuales por 25 años (300 meses).

a) Plantee la ecuación

b) Encuentre un intervalo para i donde haya un cambio de signo en la función

c) Aplique el método de Newton

1ra Evaluación II Término 2018-2019. 10/Noviembre/2018. MATG1013

Tema 2. Aproxime con un grado de exactitud de 0.0001 el valor de x que en la gráfica de y=e^x está más cerca al punto P(1,1).

a) Plantear la ecuación

b) Hallar un intervalo de existencia y de convergencia

---

Referencias: 

Gigante asteroide con su propia Luna pasará en cercanías de la Tierra . https://www.eluniverso.com/noticias/2019/05/23/nota/7344362/gigante-asteroide-su-propia-luna-pasara-cercanias-tierra

 Un asteroide dos veces más grande que un avión Boeing 747 pasará muy cerca la Tierra. https://www.eluniverso.com/noticias/2018/08/28/nota/6927335/asteroide-dos-veces-mas-grande-que-avion-pasara-muy-cerca-tierra

 

Referencia: https://spaceplace.nasa.gov/comet-quest/sp/

1ra Evaluación I Término 2018-2019. 26/junio/2018. MATG1013

Tema 2. (25 puntos) Sea g:[a,b] → R una función continua tal que g(x) ∈ [a,b] para toda x ∈ [a,b] .
Suponga además que g es una función contractiva en [a,b] esto es
\forall x,y \in [a,b]: |g(x)-g(y)| \lt |x-y|

Demuestre o refute las siguientes afirmaciones:

a) g tiene al menos un punto fijo en [a,b]

b) g tiene un punto fijo único en [a,b]

Rúbrica:
Literal a. Construye la función f(x)=x-g(x)=0 , verifica el cambio de signo de f(x) en los extremos del intervalo y concluye que p =g(p) (hasta 15 puntos),
literal b. Supone dos puntos fijos, calcula | p-q |, utiliza la propiedad contractiva y concluye que se produce una contradicción (hasta 10 puntos)

3ra Evaluación II Término 2017-2018. Febrero 20, 2018. MATG1013

Tema 1. Sea g: [a,b] →ℜe (reales) una función diferenciable tal que g(x) ∈ [a,b], para toda x ∈ [a,b]. Demuestre o refute las siguientes afirmaciones.

a) g tiene al menos un punto fijo en [a,b]

b) g tiene un punto fijo único en [a,b]