Referencia: Van Rossum 4.4 p21, Rodriguez 3.4.3.a p33, Downey 7.4
En algunos problemas existen bloques de operaciones que se repiten. Estas operaciones se pueden repetir hasta que se cumpla una condición o repetir mientras se cumpla una condición. Las estructuras de control incorporan lazos, bucles o ciclos para repetir: repita-hasta, mientras-repita (while) y «para»(for).
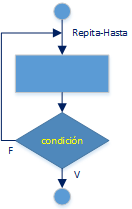
Lazo/Bucle/Ciclo: Repita-Hasta (do-while/while not)
Ejemplo: Para aprobar un curso o materia de estudio se debe superar la nota mínima para aprobar (60/100).
La condición para continuar al siguiente curso que se aplica en el Bucle se escribe como nota<60/100. En el diagrama de flujo la condición se presenta al final del bloque de operaciones, en el algoritmo en Python se escribe al inicio.
nota = 0 # nota inicial while (nota<60/100): print('tomar el curso') print('hacer el examen') nota = input('nota final:')
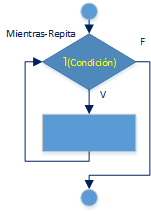
Lazo/Bucle/Ciclo: Mientras- Repita (while-do)
Ejemplo: Es el procedimiento usado en las evaluaciones para nivel o curso de idiomas (inglés).
El estudiante primero realiza un examen, si no obtiene la calificación mínima debe tomar el nivel/curso A, caso contrario puede pasar al nivel/curso B.
La condición para continuar en el lazo o bucle nota<60/100, se evalúa antes de usar el bloque de operaciones, tanto en el diagrama de flujo como en el algoritmo.
nota = 0 # nota inicial print('hacer el examen de ingles') nota = input('nota final:') while not(nota<60/100): print('tomar el curso de ingles') print('hacer el examen de ingles') nota = input('nota final:')
Para el planteamiento del ejercicio o problema al escribir el algoritmo, se selecciona el lazo “repita-hasta” o “mientras-repita” según sea más sencillo de expresar o leer en el planteamiento del ejercicio. Sin embargo, se puede intercambiar la forma del lazo usando la negación del condicional y cambiando la posición del condicional (inicio o al final).
Por ejemplo en matemáticas la expresión se lee:
f(n) \sum_1^n 1/n«sumatoria desde 1 hasta n de la expresión matemática 1/n«. En el algoritmo, se establecen los límites como desde i=1 hasta que i llegue a n,evitando que se hagan cálculos para i>n.
fn = 0 n = 4 i = 1 # desde i=1 while not(i>n): # hasta i llege a n, evite i>n fn = fn + 1/i i = i+1 print(fn)
referencia del ejercicio: 1Eva_IT2009_T1 Suma de serie con signo alternado
Recomendación: De ser necesario para continuar, revisar la sección de Conceptos Básicos, contadores y acumuladores.
Ejemplo 1
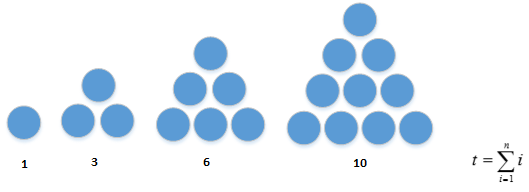
Referencia: 1Eva_IIIT2003_T2 Números triangulares
Realice un algoritmo para encontrar el término n-ésimo de la secuencia de números triangulares.
Un número triangular puede entenderse como el número de elementos usados para formar una pirámide plana, como se muestra en la figura.

Desarrollo:
Usando la analogía de la construcción de una pirámide, se observa que para construir un piso se usa un bloque, para añadir el piso 2 se usan 2 bloques, para añadir el piso 3 se usan 3 bloques, etc.
Cuántos es la variable de ingreso que indica el número de pisos que se construirán.
Para iniciar los trabajos, se anuncia la construcción del primer piso y que se han usado 0 bloques.
En el procedimiento de construcción de la pirámide, piso es una variable tipo contador; usados es una variable tipo acumulador que registra los bloques usados en la construcción de cada piso. Se construye un nuevo piso, acumulando los bloques usados hasta que se hayan construido los pisos de la variable cuántos.
La variable de salida que muestra el valor resultante es: usados.
# Ejemplo 1. Numeros triangulares # INGRESO cuantos = int(input('cuantos pisos: ')) # PROCEDIMIENTO usados = 0 piso = 1 while not(piso>cuantos): usados = usados + piso piso = piso + 1 # SALIDA print(usados)
cuantos pisos: 4 10 >>>
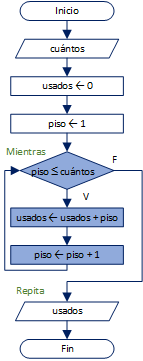
El ejemplo se desarrolló usando el lazo Repita-Hasta.
Sin embargo, si se quiere cambiar el estilo usando el lazo Mientras-Repita, se lo expresa cambiando el condicional al inicio y negando la expresión:
Repita-Hasta: (pisos>cuántos) // construir pisos hasta que // se completen los pedidos // en la variable cuántos while not(pisos>cuántos) while (pisos≤ cuántos) //Construir pisos mientras //sean menores e iguales a //los pedidos en la variable cuántos.
Ejemplo 2
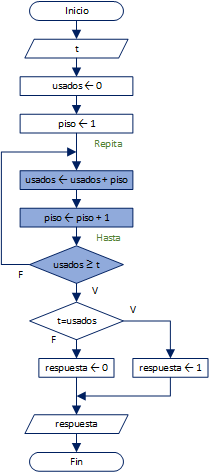
Extendiendo el ejercicio anterior, construya un algoritmo para determinar si un número t es triangular.
Para esto el lazo se debe controlar mediante el número de bloques usados comparados con el número t.
Si los usados son iguales o mayores a t, no es necesario continuar el proceso pues se obtuvo un resultado afirmativo, o los usados superan lo requerido y el número t no es triangular.
Puede mostrarse la respuesta como un valor verdadero (1) o falso (0) al comparar la igualdad entre t y usados.
La diferencia de las estructuras se puede observar entre el diagrama de Flujo anterior y el presentado.
Instrucciones en Python
# Ejemplo 2. Numero triangular # Ingreso t = int(input('número a revisar: ')) # Procedimiento usados = 0 piso = 1 while not (usados>=t): usados = usados + piso piso = piso + 1 if (t==usados): respuesta = 1 else: respuesta = 0 # Salida print(respuesta)
>>> número a revisar: 10 1 >>> número a revisar: 7 0 >>>
Propuesta: Realizar el ejercicio usando la forma mientras-repita.
Referencia: Elementos esenciales para programación: Algoritmos y Estructuras de Datos Latin Project. Primera Edición 2014. Sección 4.2. p.69