1Eva 2004-2005-2006 – Página 2 – Fundamentos de Programación

2014-03-052023-02-04

1Eva_IT2005_T1 Prueba de escritorio, algoritmo

Parcial I Término 2005 – 2006. Julio 05, 2005 /ICM00794

Tema 1. (10puntos) Para el siguiente algoritmo, muestre la prueba de escritorio para encontrar el valor final de tr siendo los valores ingresados de vu=70 y ur=4.

// Algoritmo
vu ← 0;
Mientras (vu<1)
    Ingrese (vu);
repita
ur ← 0;
Mientras (ur<1)
    ingrese (ur);
repita
tr ← 0;
mientras (ur<=vu)
    rc ← fix(vu/ur); //división entera vu/ur
    sb ← mod(vu,ur); //residuo división vu/ur
    tr ← tr+rc;
    vu ← rc+sb;
repita
mostrar (tr);

Prueba de escritorio:
vu	ur	tr	rc	sb

.
.
……	…..	……	…..	…..

2014-03-052023-02-04

1Eva_IIT2005_T1 Paridad y binario a decimal

Parcial II Término 2005 – 2006. Diciembre 06, 2005 /ICM00794

Tema 1. (20 puntos) Suponga un vector de n componentes.
Almacene en cada celda un número aleatorio binario de una cifra.

a) Determine si la cantidad de 1’s es par o impar
b) Calcule y muestre el equivalente numérico decimal del número binario almacenado.

Ejemplo:
vector(i)	1	0	0	1	1	1	0	1

cantidad de 1´s: impar
Equivalente decimal: 157₁₀

vector = [1,0,0,1,1,1,0,1]

2014-03-042023-02-04

1Eva_IIT2004_T4 Matriz de paridad

Parcial II Término 2004 – 2005. Diciembre, 2004 /ICM00794

Tema 4. (25 puntos) Se necesita transmitir una matriz de 7 filas y 7 columnas conteniendo “bits” (ceros o unos).

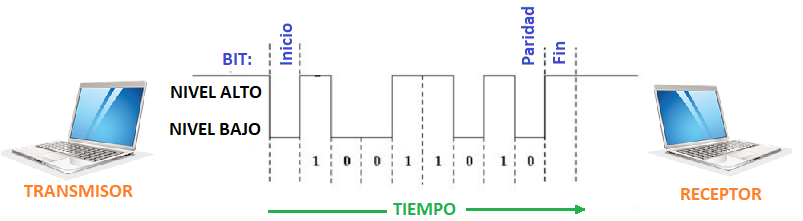
Antes de transmitirla se debe agregar una columna a la derecha conteniendo ceros o unos, de tal manera que las 7 filas tengan paridad par, es decir que la cantidad de unos en cada fila sea par. Este cero o uno adicional se denomina bit de paridad.

Realice un algoritmo que genere aleatoriamente la matriz de 7×7 llena con ceros y unos, agregue el bit de paridad en cada fila y muestre la matriz resultante.

Ejemplo: Matriz
Datos							Paridad
1	0	1	1	1	0	1	1
0	1	0	1	1	0	1	0
1	1	1	1	1	0	1	0
1	0	1	1	0	1	1	1
1	0	1	0	0	1	0	1
1	0	1	0	0	0	1	0
1	1	1	1	0	1	1	0

Ejemplo:
Para la primera fila: 1011101 1
La suma de los primeros 7 bits es 5, que es un resultado impar.

Para que la suma de toda la fila sea par se debe añadir un bit 1 adicional que es el bit de paridad.

Si suma ahora los 8 bits, incluyendo el bit de paridad, el resultado es 6 que es un número par, cumpliendo así con lo requerido.

Sugerencia: Resuelva primero para una fila, luego repita el resultado para las siguientes filas.
Referencia:
https://es.wikipedia.org/wiki/Paridad_(telecomunicaciones)

matriz = [[1,0,1,1,1,0,1,1],
          [0,1,0,1,1,0,1,0],
          [1,1,1,1,1,0,1,0],
          [1,0,1,1,0,1,1,1],
          [1,0,1,0,0,1,0,1],
          [1,0,1,0,0,0,1,0],
          [1,1,1,1,0,1,1,0]]

2014-03-042023-02-04

1Eva_IIT2004_T3 Estimar π por Montecarlo

Parcial II Término 2004 – 2005, Diciembre, 2004 /ICM00794

Tema 3. (25 puntos) Encuentre un valor aproximado de la constante π con el siguiente procedimiento.

Considere un círculo de radio unitario, centrado en el origen e inscrito en un cuadrado:

Dado el valor n, genere las coordenadas x, y para n puntos.

Asigne valores aleatorios reales entre 0 y 1 y cuente cuantos puntos caen dentro del cuadrante de círculo.

Si llamamos a este contador k, se puede establecer la siguiente relación aproximada suponiendo n grande:

\frac{k}{n} = \frac{\frac{1}{4} \text{del área del círculo}}{\frac{1}{4} \text{del área del cuadrado}}

\frac{\frac{1}{4}\pi(1)^2}{\frac{1}{4} (2)^2}=\frac{\pi}{4}

\frac{k}{n} =\frac{\pi}{4}

Donde se puede obtener el valor aproximado de π a partir de k y n.

Rúbrica: Puntos de coordenadas aleatorias dentro del cuadrado (5 puntos), verificar punto dentro del círculo (5 puntos), conteo de puntos dentro del círculo (5 puntos), calcular el valor de π (5 puntos). Algoritmo estructurado (5 puntos)

Referencia: Fontana di Trevi, https://es.wikipedia.org/wiki/Fontana_di_Trevi

2014-03-042023-02-04

1Eva_IIT2004_T2 Apuestas a números con dados

Parcial II Término 2004 – 2005. Diciembre, 2004 /ICM00794

Tema 2. (25 puntos) Simule en un algoritmo el juego descrito entre dos personas: A y B.
Muestre cuál jugador gana el juego y cuántos turnos se tuvieron que jugar.

Inicialmente cada una tiene $20
En cada turno se lanza un dado
Si sale 6 o 4, A gana $3 y B pierde $3
Si sale 2, ninguno gana ni pierde
Si sale 1, A pierde $6 y B gana $6
Si sale 3 o 5, A pierde $1 y B gana $1

El juego termina cuando una de las dos personas pierde todo su dinero.

2014-03-042023-02-04

1Eva_IIT2004_T1 Nicómano de Gerasa

Parcial II Término 2004 – 2005. Diciembre, 2004 /ICM00794

Para cada tema describa un algoritmo con un Diagrama de Flujo, Seudolenguaje , o Matlab

Tema 1. (25 puntos) Nicómano de Gerasa descubrió la siguiente propiedad de los números naturales:

Al sumar el primer impar se obtiene el primer cubo:	1 = 1
Al sumar los dos siguientes impares se obtiene el segundo cubo:	3+5 = 8
Al sumar los tres siguientes impares se obtiene el tercer cubo:	7+9+11 = 27
Al sumar los cuatro siguientes impares se obtiene el cuarto cubo:	13+15+17+19 = 64 Etc…

Con esta propiedad, para un n dado, calcule y muestre los cubos de los primeros n números naturales.

2014-03-042023-02-04

1Eva_IT2004_T4 Verificar matriz simétrica

Parcial I Término 2004 – 2005. Julio 06, 2004 /ICM00794

Tema 4. (25 puntos) Se dice que una matriz cuadrada A de orden n es simétrica, si se cumple que:

∀ i, ∀j (a_ij = a_ji) 1 ≤ i ≤n 1 ≤ j ≤n	1	2	3	4
	2	1	5	6
	3	5	1	7
	4	6	7	1

Escriba un algoritmo que permita ingresar los elementos de una matriz A con un orden n≤10 y verifique si la matriz es simétrica.

La matriz presentada es simética respecto a la diagonal, es decir matriz[f,c] = matriz[c.f]

Nota: símbolo ∀ «Para todo»

import numpy as np
matriz = [[1,2,3,4],
          [2,1,5,6],
          [3,5,1,7],
          [4,6,7,1]]

matriz = np.array(matriz,dtype=float)

El resultado debería mostrar:

"Es simétrica"
>>>

Si usa la matriz:

matriz = [[1,4,3,2],
          [2,1,5,6],
          [3,5,1,7],
          [4,6,7,1]]

matriz = np.array(matriz,dtype=float)

el resultado será:

"No es simétrica"

2014-03-042023-02-04

1Eva_IT2004_T3 Sortear parejas para tenis

Parcial I Término 2004 – 2005. Julio 06, 2004 /ICM00794

Tema 3. (25 puntos) Se tiene una lista de códigos de 25 personas de género masculino numerados del 1 al 25 y otra lista de códigos de 25 personas de género femenino numerados del 26 al 50.

a) Escriba un algoritmo para sortear parejas mixtas de tenis, tal que a cada persona de género masculino le asigne aleatoriamente una persona de género femenino. Muestre las parejas resultantes.

b) Muestre los códigos de género femenino que se encuentran en mas de una ocasión.

c) Muestre los códigos de género femenino que no aparecen en asignación alguna

2014-03-042023-02-04

1Eva_IT2004_T2 Verificar ISBN

Parcial I Término 2004 – 2005. Julio 06, 2004 /ICM00794

Tema 2. (25 puntos) El número estándar internacional de un libro (ISBN: International Standard Book Number) es un código de 10 dígitos. La última cifra es un dígito verificador que indica si el ISBN está correcto.

El dígito verificador es obtenido mediante la operación residuo de S para 11, donde S es la suma de:

una vez el primer dígito,
mas dos veces el segundo dígito,
mas tres veces el tercer dígito,
. . . ,
mas nueve veces el noveno dígito.

Ejemplo:
 la suma S para el ISBN 9684443242 es:
 1*9+2*6+3*8+4*4+5*4+6*4+7*3+8*2+9*4 = 178
 El dígito verificador es el residuo(178/11) 
 que es igual a 2.

a) Escriba un algoritmo que lea un número ISBN que verifique si éste es o no correcto.

b) Realice la prueba de escritorio de su algoritmo, utilizando el ISBN 9701702533.

Referencia: ¿Qué es un ISBN? isbn-international.org. https://www.isbn-international.org/es/content/%C2%BFqu%C3%A9-es-un-isbn

2014-03-042023-02-04

1Eva_IT2004_T1 Aleatorios en región sombreada

Parcial I Término 2004 – 2005. Julio 06, 2004 /ICM00794

Tema 1. (25 puntos) Escriba un algoritmo que genere aleatoriamente 1000 pares ordenados (x,y), donde x e y son números reales con 2 cifras decimales, tales que: franjaplano

0.00 ≤ x ≤ 4.00

0.00 ≤ y ≤ 4.00

Su algoritmo deberá determinar la cantidad de puntos que se ubicaron dentro de la región sombreada mostrada en la figura.

Rúbrica: Generar n pares aleatorios (5 puntos), verificar punto debajo de frontera superior (5 puntos), verificar punto por encima de frontera inferior (5 puntos). Conteo de puntos en franja (5 puntos). Algoritmo estructurado (5 puntos)