1Eva 2013-2014-2015 – Página 2 – Fundamentos de Programación

2016-02-052023-02-04

1Eva_IIT2015_T2 Monopolio simplificado

1ra Evaluación II Término 2015-2016. Diciembre 8, 2015 /ICM00794

Tema 2. (30 puntos) Para una versión simplificada de Monopolio con 4 jugadores se tiene que: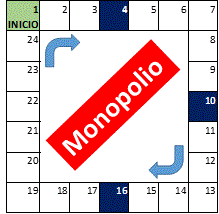

Al inicio, todos los jugadores ubican su ficha en la casilla 1 con $1500.
El tablero es de recorrido cíclico de 24 casillas.
Se juega por turnos avanzando con la suma del lanzamiento de dos dados.
Un jugador al caer en las casillas de “Casualidad” (4, 10, 16) debe pagar $100 a otro jugador escogido aleatoriamente.
Cada jugador tiene cinco casillas como “propiedades”; si un jugador cae en la propiedad de otro le deberá pagar del derecho de ocupación un valor determinado al lanzar un dado y multiplicarlo por 10.

Considere que:

El jugador 1 es propietario de las casillas 2, 8, 13, 19, 22.
El jugador 2 es propietario de las casillas 3, 7, 11, 17 y 24.
El jugador 3 es propietario de las casillas 5, 9, 15, 20 y 23.
El jugador 4 es propietario de las casillas 6, 12, 14, 18 y 21
Cada vez que un jugador pase por “Inicio” recibirá $200.

Realice un algoritmo que simule el juego hasta que uno de los jugadores quede en bancarrota (sin dinero). Al final, indique el jugador que se quedó en la bancarrota y el dinero que obtuvo cada jugador.

Rúbrica: control de saldos de jugadores y turnos (5 puntos), ubicación de jugadores (5 puntos), uso apropiado de aleatorios (5 puntos), casualidades y paso por inicio (5puntos), control de propiedades (5 puntos). Respuesta y Algoritmo estructurado (5 puntos).

2016-02-052023-02-04

1Eva_IIT2015_T1 Conjetura múltiplo de 3

1ra Evaluación II Término 2015-2016. Diciembre 8, 2015 /ICM00794

Tema 1. (25 puntos) “Si partimos de un número natural que sea múltiplo de 3 y sumamos los cubos de sus cifras, a este resultado le aplicamos la misma operación sucesivamente, llegaremos siempre al número 153.”

Elabore un algoritmo que permita ingresar un número entero de cuatro cifras que sea múltiplo de 3 y verifique si se cumple esta conjetura.

Ejemplo: 1375
 No es múltiplo de 3
 Respuesta: No cumple

Ejemplo: 1374
 Si es múltiplo de 3
 1374 → 1³ + 3³ + 7³ + 4³ = 435
 435 → 4³ + 3³ + 5³ = 216
 216→ 225 → 141 → 66 → 432 → 99 → 1458 → 702 → 351 → 153
 Respuesta: Si cumple

Referencia: https://en.wikipedia.org/wiki/Narcissistic_number. Los 153 peces en la red. Juan 21:11 NVI

Rúbrica: Ingreso y validación (5 puntos), acumular cubos de dígitos (10 puntos), control de secuencia (5 puntos). Respuesta y algoritmo estructurado (5 puntos).

2016-02-052023-02-04

1Eva_IT2015_T4 Asignar voluntarios a bloques por tipo de capacitación

1ra Evaluación I Término 2015-2016. Julio 7, 2015 /ICM00794

Tema 4. (20 puntos) Para el evento del Parque Samanes por la visita del Papa en Guayaquil el área del Parque se dividió en 32 bloques que tendrían el apoyo de voluntarios capacitados como se describe en el tema anterior.

Realice un algoritmo que reciba el listado de n voluntarios y su tipo de capacitación, resultado del tema anterior, y los distribuya para cada bloque del parque por orden de lista y de forma equitativa por tipo de capacitación.

Muestre un nuevo listado indicando los voluntarios asignados a cada bloque.

Ejemplo: para n=8, m=4, bloques=2
 El máximo por tipo de capacitación= 8/4=2
 El máximo por tipo capacitación por cada bloque = (2/2)=1

voluntario	capacita [voluntario]	bloque [voluntario]
1	3	1
2	1	1
3	4	1
4	3	2
5	1	2
6	2	1
7	2	2
8	4	2

Nota: Un voluntario solo puede atender un bloque. Suponga que n es múltiplo de m.

Sugerencia: inicie asignando solo para un tipo y un bloque, revise el tipo de capacitación de cada voluntario y asigne siempre que el conteo sea menor que máximo por tipo y bloque, caso contrario cambie de bloque, reinicie los contadores y continúe asignando con el nuevo bloque hasta completar todos los voluntarios. Repita el proceso cambiando el tipo.

Rúbrica: ingreso (5 puntos), asignar ordenadamente al bloque (10 puntos), asignar equitativamente por tipo (5 puntos)

2016-02-052023-02-04

1Eva_IT2015_T3 Capacitar a voluntarios seleccionados aleatoriamente

1ra Evaluación I Término 2015-2016. Julio 7, 2015 /ICM00794

Tema 3. (30 puntos) Se registraron voluntarios para colaborar en el evento del Parque Samanes por la visita del Papa a Guayaquil.

Para capacitar a los voluntarios, identificados por un número, se requiere formar grupos equitativos (igual cantidad) para: orientar a las personas en al ingreso y salida, portar letreros y banderas, distribuir agua, prestar atención a discapacitados y quienes pudiesen tener algún problema de salud, entre otras.

Realice un algoritmo para distribuir a n voluntarios en m tipos de capacitación en forma aleatoria, no repetida y equitativa; luego muestre el listado que indica la capacitación que recibirá cada voluntario.

Ejemplo: para n=8, m=4, maxtipo= 8/4 =2

voluntario	capacita [voluntario]
1	3
2	1
3	4
4	3
5	1
6	2
7	2
8	4

Nota: Un voluntario solo puede asistir a una capacitación. Suponga que n es múltiplo de m.

Referencia: La república. Quito y Guayaquil ultiman detalles para visita del papa Francisco a Ecuador. 02.07.2015. http://www.larepublica.ec/blog/sociedad/2015/06/30/quito-y-guayaquil-ultiman-detalles-para-visita-del-papa-francisco-a-ecuador/

Rúbrica: ingreso y validación (5 puntos), sorteo capacitación única (5 puntos), cupos de capacitación (15 puntos), mostrar resultados (5 puntos).

2016-02-052023-02-04

1Eva_IT2015_T2 Impuesto a herencia

1ra Evaluación I Término 2015-2016. Julio 7, 2015 /ICM00794

Tema 2. (25 puntos) El 5 de junio de 2015, la Asamblea Nacional recibió un proyecto de ley en materia económica con calidad de urgente conocido como “Ley de Herencias”.

El proyecto reformaría el porcentaje del impuesto sobre las herencias, el cual es progresivo basado en equivalentes al salario básico (SB). Al Año 2015, el salario básico (SB) se estableció en $354,00.

Para el impuesto, considerando solo el caso por cada heredero directo, dado un valor de herencia y el número de herederos, se calcula el valor equivalente en salarios básicos (SB). Usando la tabla se determina el rango aplicable, para calcular el impuesto se suman: el “impuesto a fracción básica” y la “tarifa” multiplicada por el excedente; el resultado buscado es el valor convertido a dólares.

Elabore un algoritmo que dado el valor de herencia, el número de herederos y el salario básico en dólares ($), calcule el valor propuesto del impuesto en dólares.

“Artículo 4. Tarifas para liquidar este impuesto son: a. En caso de los beneficiarios sea legitimarios del causante o donante, según corresponda, se aplicará la siguiente tabla:”

*Tabla expresada en número de Salarios Básicos (SB)*
Rango Aplicable		impuesto	tarifa
Fracción Básica	Exceso hasta	fracción básica	fracción excedente
–	100	–	–
100	200	–	2,50 %
200	400	2,5	7,50 %
400	800	17,5	17,50 %
800	1600	87,5	32,50 %
1600	en adelante	347,5	47,50 %

*Ejemplo:*
Valor de herencia ($)	$ 200.000,00
Número de herederos:	2
Salario básico	$ 354,00
Equivale (SB):	(200.000,00/2) /354,00= 282,4859
rango aplicable (SB)	200 a 400
Fracción Excedente (SB)	282,4859-200= 82,4859
Impuesto en SB	2,5+82,4859*(7,50%)= 8,6864
Impuesto por heredero en ($)	8,6864*$354= $3.074,99

Nota: Se usa solo un escenario para la evaluación algorítmica tomando como referencia de cálculo un literal del artículo.

Referencias: Oficio No. MINFIN-DM-2015-0333, 05-jun-2015, Quito. www.eluniverso.com. Conozca el proyecto de ley para el impuesto a las herencias en Ecuador, 2015/06/05. http://www.eluniverso.com/sites/default/files/archivos/2015/06/rd_215732correa_215732_304958.pdf

Rúbrica: ingreso (5 puntos), transformar unidades (5 puntos), determinar parámetros por rangos (10 puntos), resultado (5 puntos)

2016-02-052023-02-04

1Eva_IT2015_T1 algoritmo multiplicar

1ra Evaluación I Término 2015-2016. Julio 7, 2015 /ICM00794

Tema 1. (25 puntos) Un procedimiento matemático para multiplicar dos números enteros con valores entre 1 y 1000 se describe en el siguiente ejemplo:

Se desea conocer el producto de dos números:	997 y 991
Obtenga los resultados de las restas:	1000-997 = 3 1000-991 = 9
Sume los resultados de las restas:	3 + 9 = 12
Reste de 1000 el resultado de la suma anterior:	1000-12 = 988
Multiplique este resultado por 1000:	988 x 1000 = 988000
Multiplique los resultados de las restas iniciales:	3 x 9 = 27
La suma de los dos últimos resultados es el producto deseado:	988000+27 = 988027

Escriba un algoritmo que verifique que esta regla se cumple para cada producto a x b. Las variables a y b son enteros positivos entre 1 y un valor que puede llegar hasta 1000. Muestre la respuesta mediante un mensaje.

Rúbrica: ingreso y validación (5 puntos), procedimiento matemático (5 puntos), comprobar que cumple para a (5 puntos), comprobar que cumple para b (5 puntos), Algoritmo estructurado (5 puntos)

2015-01-142023-03-15

1Eva_IIT2014_T1 Verificar si a y b son Números amigos

1ra Evaluación II Término 2014-2015. Diciembre 9, 2014 /ICM00794

Tema 1. (20 puntos) Dos números enteros positivos a y b son amigos sí solo sí la suma de los divisores de a es igual al número b, y la suma de los divisores de b es igual al número a.

Ejemplo:
números:	a = 220	b = 284
divisores de número:	1, 2, 4, 5, 10, 11, 20, 22, 44, 55 y 110,	1, 2, 4, 71 y 142,
suma de divisores	284	220

Escriba un algoritmo para determinar si dos números enteros a y b son amigos o no.

Rúbrica: ingresar y validar positivos (5 puntos), buscar divisores (10 puntos), acumular divisores (3 puntos) determinar si son amigos (2 puntos).

2015-01-142023-02-04

1Eva_IT2014_T4 Jugadores para escuela de Fútbol

1ra Evaluación I Término 2014-2015. Julio 1, 2014 /ICM00794

Tema 4. (30 puntos) En una escuela de fútbol se inscriben n jugadores identificados con su número en la lista de asistencia y un código que identifica su mejor habilidad en la cancha. Al ingresar la habilidad por jugador, se validan los códigos.

Para entrenamiento se forman dos equipos de 11 jugadores seleccionados de forma aleatoria, cada equipo debe contener:

un portero, cuatro defensas, dos para medio campo y cuatro delanteros.

Escriba un algoritmo para ayudar a este entrenador a elegir aleatoriamente a los jugadores de ambos equipos y muestre los jugadores de cada equipo.
Observe que un jugador no puede pertenecer a más de un equipo.

Suponga que se registran siempre más jugadores por especialidad que lo necesario. Ejemplo n>40

Código	Habilidad
1	Portero
2	Defensa
3	Mediocampo
4	delantero

j	habilidad(j)	equipo(j)
1	2	0
2	2	0
3	3	2
4	1	1
5	4	0
6	4	1
…	…	…

Rúbrica: Ingreso y validación (5 puntos), selección aleatoria (5 puntos), no repetida (10 puntos), por grupos (5 puntos), salida (5 puntos)

2015-01-142023-02-04

1Eva_IT2014_T3 Pirámide Publifast

1ra Evaluación I Término 2014-2015. Julio 1, 2014 /ICM00794

Tema 3. (25 puntos) Nuevamente el juego de la pirámide fue usado como una estafa para muchos ciudadanos, en ésta ocasión usando publicidad en redes sociales.

Para demostrar que éste tipo de negocios es limitado, escriba un algoritmo que simule la situación conforme a la siguiente descripción:

Inicialmente hay una persona en la pirámide conocida como el promotor
En cada mes, para recibir los beneficios cada persona en la pirámide debe invitar un número fijo de k personas. Suponga que la pirámide crece uniforme cada mes con los invitados.
Cada persona al ingresar a la pirámide debe aportar una cuota en dólares.
El crecimiento ya no es posible cuando la cantidad de personas en la pirámide resulta ser mayor al número de personas en capacidad de aportar dinero a la pirámide. Ej: los habitantes m de un país.

Al final muestre cuántos meses funcionó la pirámide, cuántas personas formaron parte y el dinero recaudado.

Observación: La pirámide termina cuando ya no quedan suficientes nuevos aportantes. Por lo que lo recaudado es solo hasta ese mes.
Ref: http://www.eluniverso.com/noticias/2014/06/11/nota/3066307/sedujo-forma-facil-duplicar-su-dinero-web

Rúbrica: control de ciclos (5 puntos), control de crecimiento (10 puntos), resultados (10 puntos)

2015-01-142023-02-04

1Eva_IT2014_T1 Cuadrado de Cinco

1ra Evaluación I Término 2014-2015. Julio 1, 2014 /ICM00794

Tema 1. (20 puntos) Se dice que el cuadrado de cualquier número terminado en 5 se forma como el producto de las decenas y (decenas+1), añadiendo a la derecha del resultado el 25. Si el número es menor que 100 se calcula fácilmente con la tabla de multiplicar como se muestra en los ejemplos:

Operación	decena	decena+1	añadir	resultado
25²	2	3	6	625
85²	8	9	72	7225

25², la decena que es 2, se multiplica por 3 que es la decena+1, resulta 6 que se añade a la derecha 25 y su resultado es 625.

85², se calcularía como 8×9=72, se añade a la derecha 25, el resultado es 7225.

Elabore un algoritmo que valide el proceso para los números terminados en cinco dentro del rango entre 5 y m (ejemplo 1000). Al final muestre si se cumple lo descrito, en caso de ser incorrecto, mostrar el primer número para el que no se cumple.

Rúbrica: Operaciones con los dígitos (10 puntos), Validación rango (10 puntos).