Publicado en

2Eva_IIT2011_T3 Movimientos del caballo en ajedrez sobre una matriz/arreglo

2da Evaluación II Término 2011-2012, Enero 31, 2012 /ICM00794

Tema 3. (25 puntos)

En un tablero de ajedrez (8×8 casillas), la ficha del caballo puede moverse entre casillas, siguiendo las siguientes reglas:

  • Las direcciones se consideran horizontales o verticales.
  • Se mueve dos casillas en una dirección, y luego una casilla en cualquier dirección perpendicular al movimiento anterior.

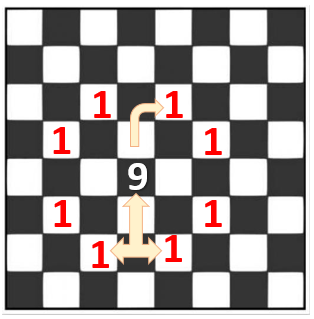
En la figura se muestra un ejemplo de la ubicación del caballo con el número 9 y las casillas donde se puede mover se marcan con 1.

muevecaballo(5,4)


a) Realice una función muevecaballo(f,c) que reciba las coordenadas de la ubicación del caballo en el tablero de ajedrez, asigne el valor de 1 a las casillas en las cuales puede moverse y entrega la matriz resultante.

Nota: considerar los límites del tablero y que el tablero esta ocupado solo por el caballo.

b) Escriba un programa que:

  • genere una matriz contrincante con la función ubicaficha(6,8) del tema anterior,
  • solicite las coordenadas f y c del caballo en el tablero,
  • genere otra matriz tablero con la función muevecaballo(f,c), y
  • simule el juego contando y mostrando los números que el caballo puede atacar en la matriz contrincante.

Rúbrica: Definición de función (5 puntos), ubicación de movimientos (10 puntos), Programa (10 puntos).

Referencia: Ajedrez – El caballo – 02: Explicación del movimiento del caballo

 

Publicado en

2Eva_IIT2011_T1 Algoritmo de Euclides MCD

2da Evaluación II Término 2011-2012, Enero 31, 2012 /ICM00794

Tema 1 (20 puntos). El Algoritmo de Euclides es considerado el más antiguo y no trivial para encontrar el “máximo común divisor” (mcd) entre dos números a y b.
El paso esencial que garantiza la validez del algoritmo consiste en mostrar que el mcd de a y b es:

  • considerar que a > b  y b≥0
  • si b es cero, mcd es igual a a
  • en otro caso, si b>0, es igual al mcd entre b y el residuo de a dividido por b

Realice una función recursiva mcdeuclides(a,b) siguiendo el algoritmo de Euclides, y muestre una prueba de escritorio para a=15 y b=6.

Rúbrica: Definición de función (5 puntos), Recursividad (10 puntos), Prueba de escritorio (5puntos).

Prueba de escritorio:

>>> mcd_euclides(15,6)
a:  15 b:  6 residuo: 3
a:  6 b:  3 residuo: 0
3
>>> mcd_euclides(72,16)
a:  72 b:  16 residuo: 8
a:  16 b:  8 residuo: 0
8
>>>
Publicado en

2Eva_IT2011_T4 Números Romanos a decimal

2da Evaluación I Término 2011, Agosto 30, 2011 /ICM00794

Tema 4 (25 puntos). Realice un programa que reciba una cadena de caracteres, que representa un número romano y la convierta a número en base decimal.

El equivalente de números romanos se muestra en la tabla, y para la conversión considere solo las siguientes reglas:

 Tabla de equivalentes
Romano I V X L C D M
Decimal 1 5 10 50 100 500 1000
  • Si a la derecha de una cifra romana de escribe otra igual o menor, el valor de ésta se suma a la anterior.
  • Si entre dos cifras romanas cualesquiera existe otra menor, ésta restará su valor a la siguiente. Casos para I, X y C
  • En ningún número se puede poner una misma letra más de tres veces seguidas.
  • Suponga que la cadena de caracteres corresponde a un número romano válido.
Ejemplos:
Romano: CLXIII C L X I I I
Decimal: 163 +100 +50 +10 +1 +1 +1
Romano: CXLIX C X L I X
Decimal: 149 +100 -10 +50 -1 +10

Rúbrica: cálculo de equivalencias aditivas (10 puntos), equivalencias con signo menos (15 puntos)

Publicado en

2Eva_IT2011_T3 Cuadrado semimágico

2da Evaluación I Término 2011, Agosto 30, 2011 /ICM00794

Tema 3 (25 puntos). Llamemos cuadrado «semi-mágico» a una matriz cuadrada conteniendo números de tal manera que cada suma parcial de la primera fila, última fila, primera columna, última columna y cada una de las dos diagonales, producen el mismo resultado.

Ejemplo:
1 3 6 2 = 12
7 4 1 4
1 6 4 3
3 4 2 3 = 12
 =  =  =
12 12 12 12

Escriba un programa que solicite: el tamaño n del cuadrado y el máximo de intentos a realizar, para llenar aleatoriamente una matriz de nxn con enteros positivos de una cifra, hasta que la matriz sea un cuadrado «semi-mágico».

Muestre la matriz resultante y la cantidad de intentos realizados, si se logró el objetivo.

Rúbrica: generación de matriz (5 puntos), determinar si es semi-mágico (15 puntos), control de intentos y resultados (5 puntos)

Publicado en

2Eva_IT2011_T2 Votar por nombre del puente

2da Evaluación I Término 2011, Agosto 30, 2011 /ICM00794

Tema 2 (35 puntos). Al finalizar la construcción del Cuarto Puente, el Ministerio de Transporte y Obras Públicas nombrará al complejo vial mediante votaciones electrónicas entre cuatro nombres.

Realice un programa que permita administrar las votaciones mediante el siguiente menú:

  1. Ingresa y valida voto.- se registra cédula, nombre y voto. Se descarta el registro si el voto es repetido; puede validar usando la función del tema anterior.
  2. Muestra registrados y descartados. – Presenta los contadores de votos registrados y descartados por reintento del votante.
  3. Resultado de votación.- Muestra los resultados de la votación y el ganador.
  4. Salir.
Ejemplo de Nombres:
 (1) Unidad Nacional
 (2) Carlos Pérez Perazo
 (3) Rafael Mendoza Avilés
 (4) Otro por presentar….

Sugerencia: Pedir los datos y registrarlos solamente si vota por primera vez. Copiar las cédulas válidas en un vector y usar la función enlista(,) del tema anterior para validar las cédulas repetidas.
Referencia: “Un concurso eliminará los nombres de tres viaductos” www.eluniverso.com – 30. Agosto. 2011

Rúbrica: Menú (5 puntos). Definición y uso de estructura de datos (5 puntos). Validación de votos y uso de función (10 puntos). Mostrar registrados y descartados (5 puntos). Resultados de votación (10 puntos)  

Publicado en

2Eva_IT2011_T1 Buscar valor en lista

2da Evaluación I Término 2011, Agosto 30, 2011 /ICM00794

Tema 1 (15 puntos). Realice una función enlista(número,vector) que reciba un número entero y un vector que contiene una lista de números, revise si el número se encuentra en el vector.
Las respuestas serán: si esta en lista (1), si no está en lista (0).

i vector(i)
1 456
2 654
3 234
4 987
5 876 
Ejemplo:
>> enlista(789,vector)
 ans= 0
>> enlista(234,vector)
 ans=1

Rúbrica: Definición de función (5 puntos), revisión (5 puntos), respuestas (5 puntos)

 

Publicado en

2Eva_IIT2010_T4 Elegir representante con 50% votación

2da Evaluación II Término 2010, Febrero 01, 2011 /ICM00794

Tema 4 (30 puntos). Un grupo de n personas debe elegir a su representante.

Será elegido si tiene al menos la mitad de los votos, caso contrario se deberá repetir la votación desde el inicio.

Cada persona es identificada con un número entero entre 1 y n y cualquiera de las personas puede ser elegida.

Escriba un programa para el proceso electoral con el siguiente menú:

  1. Inicializar votación: Poner contadores y registros de n votos en cero para nueva votación.
  2. Ingresar los votos: se ingresa el número identificador del votante y luego el identificador de su candidato. Validar que el votante realice un solo voto.
  3. Determinar ganador: si lo hubo, mostrar cuál fue y si la votación cumple con mayoría requerida.
  4. Mostrar estado de votación: Muestra cantidad de votos realizados y la cantidad que aún no votan.
  5. Salir

Sugerencia: Use un vector de n componentes para almacenar el conteo de votos de cada una de las n personas. Utilice otro vector para registrar quienes ya han votado.

Rúbrica: Menú (5 puntos). Ingreso y validación (10 puntos). Ganador y validar mayoría (10 puntos). Mostrar estado (5 puntos).

 

Publicado en

2Eva_IIT2010_T3 Validar registro de revocatoria en CNE

2da Evaluación II Término 2010, Febrero 01, 2011 /ICM00794

Tema 3 (25 puntos). El Consejo Nacional Electoral (CNE) para iniciar un proceso de revocatoria de mandato de alcaldes, requiere en la solicitud la presentación de al menos el 10% de firmas del registro electoral.

Para realizar la revisión de los datos presentados para este proceso se dispone de:

  • Las cédulas del padrón en un arreglo de tamaño n
  • Las cédulas de solicitantes de la revocatoria en un arreglo lista de tamaño m

a) Realice una función registrados(padrón, lista) que indique cuántas de las cédulas de la lista están registradas en el padrón. Suponga que no hay datos repetidos.

i Padrón(i) j lista(j)
1 0912345678 1 0987654321
2 0987654321 2 0567896543
3 0754321234 … …
4 0765432456 m
5 0567896543
… …
n

b) Realice un programa que solicite el ingreso de los arreglos padrón y lista, usando las funciones únicos() del tema anterior y registrados() , valide los datos de la lista para informar si los datos cumplen con al menos el 10% del padrón.

Referencia: “11 procesos de revocatoria se decidirán en febrero”. Enero 12, 2011. – “El presidente del CNE sugiere una reforma para normar la revocatoria”. Diciembre 16, 2011. http://www.eluniverso.com

Rúbrica: Definición y uso de las funciones (10 puntos). Algoritmo “registrados” (10 puntos). Programa integral (5 puntos)

 

Publicado en

2Eva_IIT2010_T2 Mostrar valores únicos en vector

2da Evaluación II Término 2010, Febrero 01, 2011 /ICM00794

Tema 2 (20 puntos) Realice la función únicos(vector) que recibe un vector de n enteros y entrega otro vector conformado por los elementos no repetidos.

Considerar que el tamaño del vector resultante puede ser menor al tamaño del vector ingresado.

i vector(i) j resultado(j)
1 12345 1 12345
2 64279 2 64279
3 12345 3 74351
4 74351 4 67531
5 12345 m 5 76524
6 67531
n 7 76524

Rúbrica: Definición de la función (5 puntos). Determinar elementos no repetidos (5 puntos). Vector sin elementos repetidos (10 puntos).

vector = [12345, 64279, 12345, 74351, 12345, 67531, 76524]
unicos = [12345, 64279, 74351, 67531, 76524]
Publicado en

2Eva_IIT2010_T1 Juego con fichas rojas y azules

2da Evaluación II Término 2010, Febrero 01, 2011 /ICM00794

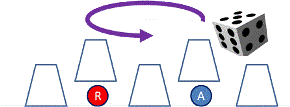Tema 1 (25 puntos) El “Juego Lucky” utiliza cuatro fichas rojas (‘R’), una ficha azul (‘A’) y un dado.

  • LuckySe cubren cada ficha con un vaso y aleatoriamente se alinean los vasos.
  • Al reemplazar la ficha azul por el valor del dado y las rojas por 0 se formará un número equivalente.
  • El jugador puede realizar dos cambios de posición entre los vasos sin levantarlos.
  • Al cambiar las posiciones se informa al jugador si el número equivalente: aumentó, es igual o disminuyó.
  • Al final, se descubren las fichas mostrando los puntos logrados, formado por el número equivalente.

a) Realice una función puntos(cadena,valor) que reciba una cadena de caracteres entre ‘R’ y ‘A’, reemplace la letra ‘R’ por 0 y la letra ‘A’ por valor, entregue el equivalente numérico de puntos obtenidos.

b) Escriba un programa que simule el juego preguntando cuántas rondas se jugarán, al final mostrará los puntos acumulados por el jugador.

Ejemplo:
>> puntos('RRRAR',5)
 ans = 50
>> puntos('RARRR',5)
 ans = 5000

Nota: Utilice una cadena de caracteres para simular las fichas y sus posiciones.

Rúbrica: Definición y uso de función (10 puntos). Cambio de posiciones (5 puntos). Mostrar cambios de valor (5 puntos). Programa integral (5 puntos)