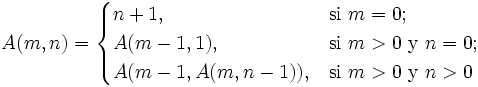3Eva 2004-2005-2006 – Fundamentos de Programación

2015-01-112023-02-04

3Eva_IIT2006_T1 Crear usuarios en lista de nombres

3ra Evaluación II Término 2006-2007, Febrero 6, 2007 /ICM00794

Tema 1. (20 Puntos) Los “nombres de usuario” para una compañía se crean a partir de los nombres y el apellido paterno de sus empleados conformado de ocho (8) letras, usando una letra de cada nombre y el resto de su apellido.

a) Realice una función en matlab user(nombre1,nombre2,apellidop) que reciba los nombres y apellido paterno de un empleado y devuelva su “nombre de usuario”.

b) Escriba un programa en Matlab que registre en una lista los nombres de los n empleados de la compañía y muestre el listado de los “nombres de usuario”

Ejemplo:
Nombre1	Nombre2	Apellido Paterno	Usuario
Juan	Pedro	Rodriguez	jprodrig

2014-03-112022-07-30

3Eva_IIT2006_T4 Beneficiarios de Bono Desarrollo Humano

3ra Evaluación II Término 2006-2007, Febrero 6, 2007 /ICM00794

Tema 4. (30 puntos) El Bono de Desarrollo Humano se ofrece a madres solteras, ancianos y discapacitados, de los cuales se registra los nombres, apellidos, provincia, ciudad y tipo.

Realice un programa para ayudar al Ministerio de Bienestar social para gestionar el registro de los beneficiarios y que tenga el siguiente menú:

1. Ingresar un beneficiario Nombre, apellido, provincia, ciudad, tipo y pagado.
2. Mostrar el número de registrados por provincia
3. Mostrar el número de registrados por tipo
4. Mostrar el total de beneficiarios, y el monto por pagar.
5. Salir

Ejemplo de lista de beneficiarios:
Nombre	Apellido	Provincia	Ciudad	Tipo	Pagado
Juan	Piguave	Guayas	Playas	(2) Anciano	0
Maria	Gomez	Manabí	Manta	(1) Madre Soltera	30
Pedro	Guerra	Pichincha	Sto. Domingo	(3) Discapacitado	30

Nota: Puede codificar a número las provincias y el tipo de beneficiario para facilitar el conteo.

2014-03-112022-07-30

3Eva_IIT2006_T3 Números Primos más cercanos

3ra Evaluación II Término 2006-2007, Febrero 6, 2007 /ICM00794

Tema 3. (30 Puntos) Dada una lista de n números, obtener el número primo más cercano a cada uno de los números. En caso de que el número de la lista sea un número primo, ese número es el más cercano.

a) Escriba una función primo(n) que determine si el numero n es primo.

b) Realice un programa que revise de una lista, los números enteros, los inmediatos inferiores y superiores hasta encontrar un número primo y llene la tabla resultante.

*Ejemplo: Sea* n = 6
Números		Primo superior	Primo inferior
100	→	101	97
246	→	251	241
2	→	2
333	→	337	331
2007	→	2011	2003

2014-03-112022-12-17

3Eva_IIT2006_T2 Generar triángulo de Pascal

3ra Evaluación II Término 2006-2007, Febrero 6, 2007 /ICM00794

Tema 2. (20 Puntos) El triángulo de Pascal, es un triángulo de números enteros, infinito y simétrico.

Se genera de arriba hacia abajo con la propiedad de que sus extremos siempre son 1, y que sus números interiores son la suma de los dos inmediatos superiores.

Escriba un programa en matlab que genere un triángulo de Pascal para n filas, y muestre la suma de sus números pares.

Sugerencia: Usando una matriz cuadrada, en la primera columna y la diagonal llene de unos. Luego realice las operaciones en la parte triangular inferior.

2014-03-112022-07-30

3Eva_IT2006_T4 Juego planta bombas (buscaminas)

3ra Evaluación I Término 2006-2007, Septiembre 12, 2006 /ICM00794

Tema 4. (30 puntos) Un juego de guerra consiste en delimitar el área del enemigo para ser explorada por paracaidistas en ejercicios de prueba y error.

El enemigo planta bombas en el área para protección a prueba de paracaidistas.

El juego consiste en enviar un paracaidista a una coordenada del área enemiga y si aterriza exitosamente, explore el área a su alrededor e informe al centro de comando, cuántas bombas existen alrededor de su coordenada.

a) Realice una función plantabombas(m, n) que dada una cantidad de m bombas, coloque en el área definida por una matriz cuadrada de tamaño n las bombas de manera aleatoria y no repetida.
Considere que m siempre es menor que n².

b) Realice un programa, que pida las coordenadas de aterrizaje de un paracaidista, utilice la función del tema anterior, valide si el paracaidista logro llegar a salvo, e informe de cuantas bombas existen a su alrededor.

Nota: Las coordenadas no pueden ser de los límites de la matriz.

x\y	1	2	3
1	0	1	1
2	0	paracaidista	0
3	1	0	1
4

Bombas cercanas a matriz[2,2]=4

2014-03-112022-07-30

3Eva_IT2006_T3 Tabular cuotas y saldo de deuda

3ra Evaluación I Término 2006-2007, Septiembre 12, 2006 /ICM00794

Tema 3. (25 puntos) Una empresa de venta y financiación de vehículos ofrece a sus clientes planes de pago con cuotas mensuales.

El vendedor dispondrá de un programa que calcule la cantidad de meses que le tomará a su cliente pagar la totalidad de la deuda de acuerdo a los parámetros definidos.

p: Precio de Vehículo
r: Tasa de interés mensual en porcentaje
cuota: Cuota mensual

a) Realice una función saldo(r, cuota, saldoanterior) que calcule el saldo mensual conociendo la tasa de interés, la cuota y el saldo anterior.

b) Realice un programa que usando la función saldo, determine en cuántos meses el cliente terminaría de pagar su deuda.

Mes	Intereses	Cuota	Saldo
0	–	–	8.000,00
1	80,00	300,00	7.780,00
2	77,80	300,00	7.557,80
3	75,58	300.00	saldo
4	…	…	0

2014-03-112022-07-30

3Eva_IT2006_T2 Intercalar palabras pastestring(a,b,p)

3ra Evaluación I Término 2006-2007, Septiembre 12, 2006 /ICM00794

Tema 2. (25puntos) Implemente una función en matlab llamada PasteString(a, b, p) que dadas dos cadenas a y b, inserte después de la posición p de primera, a la segunda cadena y retorne la nueva cadena.

Ejemplo:
Si la primera cadena es “FUNDAMENTOS”, 
la segunda “PROG” y p es 4, 
el resultado será “FUNDPROGAMENTOS”

2014-03-112022-12-17

3Eva_IT2006_T1 Ackerman recursiva

3ra Evaluación I Término 2006-2007, Septiembre 12, 2006 /ICM00794

Tema 1. (20puntos) Debido a su definición, profundamente recursiva, la función de Ackermann se utiliza con frecuencia para comparar compiladores en cuanto a su habilidad para optimizar la recursión. Dicha función se define a continuación:

a) Realice una función ackerman(m, n) en matlab, que encuentre el resultado de Ackerman para n y m dados.

b) Realice la prueba de escritorio para ackerman(1, 2).

2014-03-092022-12-17

3Eva_IT2005_T4 Tabla de Pozo millonario

Mejoramiento I Término 2005 – 2006. Septiembre 13, 2005 /ICM00794

Tema 4 (15 puntos) En el juego del Pozo Millonario, similar al juego de bingo, una tabla se genera con 15 números aleatorios entre 1 y 25.

Realice un algoritmo para generar una tabla de Pozo Millonario considerando que:

Los números en la tabla NO son repetidos
Los números se presentan ordenados de forma ascendente

Referencia: http://www.loteria.com.ec

Rúbrica: Números NO repetidos (10 puntos). Presentados ordenados en forma ascendente (5 puntos).

2014-03-092022-12-17

3Eva_IT2005_T3 Calcular millas de viajero

Mejoramiento I Término 2005 – 2006. Septiembre 13, 2005 /ICM00794

Tema 3. (30 puntos).Para el cálculo de las millas de viajero frecuente promocionadas por las aerolíneas, se requiere las coordenadas cartesianas de un mapa que corresponden a las ciudades entre las que el viajero usa un boleto.

a) Escriba una función distancia(x₁,y₁,x₂,y₂) que dados dos puntos cartesianos, que retorne la distancia entre ellos.

b) Escriba un programa que en una estructura almacene los nombres de las ciudades y los puntos (x,y) por donde el viajero inicia su viaje, sigue su recorrido y retorna a su ciudad de origen y calcule, la distancia total recorrida entre todos los puntos usando la función distancia.

Ciudad	X	Y	Distancia Recorrida
Guayaquil	0	0	0
Riobamba	5	1	5.099
Quito	4	3	2.236
Manta	1	2	3.162
Guayaquil	0	0	2.236
Millas Acumuladas:			12.733