Categoría: Soluciones

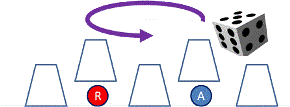
Ejercicio: 2Eva_IIT2010_T1 Juego con fichas rojas y azules

literal a

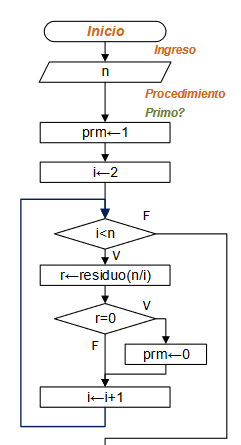
usar la posición relativa para determinar el valor de potencia de 10 para acumular el total al recorrer la cadena.

intercambiar a: 1
 con b: 3
cadena inicial:  RRRAR
puntos vasos sin mover:  30
cadena nueva:  RRRAR
puntos vasos movidos:  30
>>> 
 RESTART: D:/CCPG1001Ejemplos/fichasrojasazules.py 
intercambiar a: 2
 con b: 4
cadena inicial:  RRRAR
puntos vasos sin mover:  30
cadena nueva:  RARRR
puntos vasos movidos:  3000
>>> 

literal b

desarrollado hasta intercambiar caracteres entre las posiciones a,b

Tarea: realizar varias «rondas»

Instrucciones Python

# 2Eva_IIT2010_T1 Juego con fichas rojas y azules
import random as rnd

# literal a
def puntos(cadena,valor):
    n = len(cadena)
    total = 0
    for i in range(0,n,1):
        base = 10**(n-1-i)
        if cadena[i]=='A':
            total = total + valor*base
        if cadena[i]=='R':
            total = total + 0*base
    return(total)

# literal b
def intercambia(cadena,a,b):
    n = len(cadena)
    orden = []
    for i in range(0,n,1):
        orden.append(i)
    orden[a-1] = b-1
    orden[b-1] = a-1
    nueva = ''
    for i in range(0,n,1):
        posicion = orden[i]
        nueva = nueva + cadena[posicion]
    return(nueva)

# INGRESO
a = int(input('intercambiar a: '))
b = int(input(' con b: '))

n = 5 # cantidad de vasos

# PROCEDIMIENTO
dado = int(rnd.random()*6)+1
cadena = ''
for i in range(0,n,1):
    if i == dado:
        cadena = cadena + 'A'
    else:
        cadena = cadena + 'R'

equivale = puntos(cadena,dado)

nueva = intercambia(cadena,a,b)
equivale2 = puntos(nueva,dado)

# SALIDA
print('cadena inicial: ',cadena)
print('puntos vasos sin mover: ',equivale)
print('cadena nueva: ',nueva)
print('puntos vasos movidos: ',equivale2)

Ejercicio: 1Eva_IIT2010_T3 Juego del amigo secreto

Propuesta de solución en Python: py_pdf, tambien en matlab: m_pdf

Inicie el sorteo con banderas de amigo/amiga en cero,

AmigA = np.zeros(n+1,dtype=int)
AmigO = np.zeros(2*n+1,dtype=int)

para poner luego el valor sorteado a cada uno, si aún no se ha repetido.

dama = int(rnd.random()*n)+(n+1)

El valor repetido se verifica revisando el estado del arreglo en la posición correspondiente, esperando que sea vacio AmigO[dama]==0, solo allí se asigna el amigo y se pasa al siguiente sorteo.

# sortea dama para cada AmigO
i = 1
while (i<=n):
    dama = int(rnd.random()*n)+(n+1)
    if (AmigO[dama]==0):
        AmigO[dama] = i
        i = i+1

ser repite el mismo proceso para el otro género.

---

Instrucciones en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2010_T3 Juego del amigo secreto
# Propuesta de solucion. edelros@espol.edu.ec

import numpy as np
import random as rnd

# INGRESO
n = int(input('¿número de parejas?: '))

# PROCEDIMIENTO
AmigA = np.zeros(n+1,dtype=int)
AmigO = np.zeros(2*n+1,dtype=int)

# sortea dama para cada AmigO
i = 1
while (i<=n):
    dama = int(rnd.random()*n)+(n+1)
    if (AmigO[dama]==0):
        AmigO[dama] = i
        i = i+1

# sortea caballero para cada AmigA
j = n+1
while (j<=(2*n)):
    caballero = int(rnd.random()*n)+1
    if (AmigA[caballero]==0):
        AmigA[caballero] = j
        j = j+1

# SALIDA
print('pareja de caballeros')
i = 1
while (i<=n):
    print(i,' , ',AmigA[i])
    i = i+1
    
print('pareja de damas')
j = n+1
while (j<=(2*n)):
    print(j,' , ',AmigO[j])
    j = j+1

Resultado del algoritmo

¿número de parejas?: 4
pareja de caballeros
1  ,  5
2  ,  8
3  ,  7
4  ,  6
pareja de damas
5  ,  3
6  ,  4
7  ,  1
8  ,  2
>>> 

---

Diagrama de Flujo

ejercicios resueltos Python 1eva_iit2010_t3 pdf

ejercicios resueltos Matlab 1eva_iit2010_t3 pdf

Ejercicio: 1Eva_IIT2010_T2 Venta de pasajes tren turístico

Solución propuesta:  py_pdf, versión matlab m_pdf

Inicialmente desarrolle la venta para un solo pedido/comprador, así encontrará las partes principales de la venta y hace el primer esquema del procedimiento a seguir.

pedido = int(input('¿cuántos pasajes?: '))
print('   Monedas: 1.Dolar 2.Euro 3.Peso')
moneda = int(input(' ¿Tipo Moneda?: '))
cantidad = float(input(' ¿Cantidad de Dinero?: '))

if (moneda==1):
    valor = cantidad*pesodolar
if (moneda==2):
    valor = cantidad*pesoeuro
if (moneda==3):
    valor = cantidad

pago=pedido*precio

En una segunda versión, agregue las demás opciones de control, tales como contadores y acumuladores para controlarlos turnos o la venta de asientos del tren.

En este proceso se añade un lazo para repetir, y se termina mostrando los resultados de boletos vendidos, el dinero cobrado y el total devuelto.

Tarea: Prestar atención en la venta cuando quedan pocos boletos y el usuario quiere comprar más de los que están disponibles

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2010_T1 Venta de pasajes tren turístico
# Propuesta: edelros@espol.edu.ec

turnomax = int(input('¿cuántos turnos?: '))
capacidad = int(input('capacidad del tren?: ')) 

pesodolar = 2.50
pesoeuro  = 3.25
precio    = 7.00
vendido   = 0
cobrado   = 0.00
devuelto  = 0.00

turno = 1
while (turno<=turnomax and vendido<=capacidad):
    print('Turno:')
    print(turno)
    pedido = int(input('¿cuántos pasajes?: '))
    print('   Monedas: 1.Dolar 2.Euro 3.Peso')
    moneda = int(input(' ¿Tipo Moneda?: '))
    cantidad = float(input(' ¿Cantidad de Dinero?: '))

    if (moneda==1):
        valor = cantidad*pesodolar
    if (moneda==2):
        valor = cantidad*pesoeuro
    if (moneda==3):
        valor = cantidad

    pago=pedido*precio
    if (pago<=valor and((vendido+pedido)<capacidad)):
        vendido = vendido+pedido
        cobrado = cobrado+pago
        cambio  = valor-pago
        devuelto = devuelto+cambio

        print('Se vendieron Boletos: ')
        print(pedido)
        print('su cambio: ')
        print(cambio)
    else:
        print('no es dinero suficiente')

    turno = turno + 1

# SALIDA
print('pasajes vendidos: ')
print(vendido)
print('pesos cobrados: ')
print(cobrado)
print('pesos devueltos: ')
print(devuelto)

Resultado del algoritmo

¿cuántos turnos?: 3
capacidad del tren?: 50
Turno:
1
¿cuántos pasajes?: 3
   Monedas: 1.Dolar 2.Euro 3.Peso
 ¿Tipo Moneda?: 1
 ¿Cantidad de Dinero?: 20
Se vendieron Boletos: 
3
su cambio: 
29.0
Turno:
2
¿cuántos pasajes?: 4
   Monedas: 1.Dolar 2.Euro 3.Peso
 ¿Tipo Moneda?: 2
 ¿Cantidad de Dinero?: 20
Se vendieron Boletos: 
4
su cambio: 
37.0
Turno:
3
¿cuántos pasajes?: 2
   Monedas: 1.Dolar 2.Euro 3.Peso
 ¿Tipo Moneda?: 3
 ¿Cantidad de Dinero?: 30
Se vendieron Boletos: 
2
su cambio: 
16.0
pasajes vendidos: 
9
pesos cobrados: 
63.0
pesos devueltos: 
82.0
>>> 

Diagrama de Flujo

 

 

ejercicios resueltos Python 1eva_iit2010_t2 pdf ejercicios resueltos Matlab 1eva_iit2010_t2 pdf

Ejercicio: 1Eva_IIT2010_T1 Censo de instrucción por género

Propuesta de solución en Python: py_pdf, también en matlab: m_pdf

Los datos se almacenan en vectores y se los tabula/cuenta en una matriz.  Las filas representan la instrucción y columna el género.

Lista de género y nivel de instrucción:

i	Género [i]	Instrucción [i]	Género: 1. Masculino 2. FemeninoInstrucción: 1. Primaria 2. Secundaria 3. Superior
1	1	2
2	2	3
3	1	3
…	…	…
n	…	…

Se usará desde la casilla 1, por lo que el tamaño del arreglo es n+1 al no usar la casilla cero.

n = int(input('¿Cuántos formularios: '))

genero = np.zeros(n+1,dtype=int)
instruccion = np.zeros(n+1,dtype=int)
i = 1
while not(i>n):
    print('Formulario:',i)
    genero[i] = int(input('  genero: '))
    instruccion[i] = int(input('  instruccion: '))
    i = i+1

Se inicializan los contadores al inicializar la matriz para luego procesar los datos de todos los formularios registrados.

Instrucción por género:

	Masculino	Femenino
Primaria
Secundaria
Superior

Para facilitar la lectura del algoritmo se usan como variables f y c para referenciar las filas y columnas. Una forma más larga de solución podría usar contadores individuales para contar primaria/masculino, primaria/femenino, etc.

Tarea: validar el ingreso de género e instrucción por cada formulario

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2010_T1 Censo de instrucción por género
# propuesta: edelros@espol.edu.ec

import numpy as np

#INGRESO
n = int(input('¿Cuántos formularios: '))

genero = np.zeros(n+1,dtype=int)
instruccion = np.zeros(n+1,dtype=int)

i = 1
while not(i>n):
    print('Formulario:',i)
    genero[i] = int(input('  genero: '))
    instruccion[i] = int(input('  instruccion: '))
    i = i+1

# PROCEDIMIENTO
tabla = np.zeros(shape=(3+1,2+1),dtype=int)
i = 1
while not(i>n):
    f = instruccion[i]
    c = genero[i]
    tabla[f,c] = tabla[f,c]+1
    i = i + 1

# SALIDA
print('Instr  M  F ')
f = 1
while not(f>3):
    c = 1
    cadena = ''
    while not(c>2):
        cadena = cadena+' '+str(tabla[f,c])
        c = c + 1
    print('   '+str(f)+': '+cadena)
    f = f + 1

Resultado del algoritmo

¿Cuántos formularios: 5
Formulario: 1
  genero: 1
  instruccion: 2
Formulario: 2
  genero: 1
  instruccion: 2
Formulario: 3
  genero: 2
  instruccion: 1
Formulario: 4
  genero: 2
  instruccion: 1
Formulario: 5
  genero: 2
  instruccion: 3
Instr  M  F 
   1:  0 2
   2:  2 0
   3:  0 1
>>> 

---

Diagrama Flujo Mientras-Repita

ejercicios resueltos Python 1eva_iit2010_t1 pdf

ejercicios resueltos Matlab 1eva_iit2010_t1 pdf

Ejercicio: 2Eva_IT2010_T3 Registrar donantes ONTOT

Propuesta de solución en Python: py_pdf, también en versión matlab: m_pdf

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 2Eva_IT2010_T3 Registrar donantes ONTOT
# propuesta solucion: edelros@espol.edu.ec

import numpy as np
donante = []

opcion = 0
while not(opcion==5):
    print('1. Ingreso de donantes ')
    print('2. Ingresar estado con prueba medica')
    print('3. Consulta por estado de donantes ')
    print('4. Total de donantes/tipo de sangre')
    print('5. Salir')

    opcion = int(input('cual opcion:'))

    if (opcion==1):      
        print('1. Ingreso de donantes ')
        texto  = input('nombre: ')
        numero = input('cedula: ')
        numb   = int(input('anio nacimiento:'))
        print('(1)O-, (2) O+, (3) A-, (4)A+, (5)B-, (6)B+, (7)AB-, (8)AB+')
        sangre = int(input('tipo sanguineo:'))

        estado = 1
        # crea el registro para un donante
        registro = {'nombre':texto,'cedula':numero,
                    'nacim':numb, 'tipos':sangre,
                    'estado':1}
        
        # añade el registro a la tabla donante
        donante.append(registro)

        
    if (opcion==2):
        print('2. Ingresar estado con prueba medica')
        quien  = int(input('cual numero de donante:'))
        cuanto = int(input(' (2) Aceptado , (3) Rechazado :'))
        donante[quien]['estado'] = cuanto
        
    if (opcion==3):
        print('3. Consulta por estado de donantes ')
        cual = int(input('cual estado: '))
        fila = 0
        
        # tamaño de la tabla donante
        n = len(donante)
        while not(fila>=n):
            if (cual==donante[fila]['estado']):
                print(donante[fila]['nombre'])
            fila = fila + 1
        
    if (opcion==4):
        print('4. Total de donantes/tipo de sangre')

        # No se usará la fila 0 de veces
        veces = np.zeros(8+1,dtype=int)
        fila = 0
        while (fila<n):
            k = donante[fila]['tipos']
            veces[k] = veces[k] + 1
            fila = fila + 1
        
        print(veces)
        
    if (opcion==5):
        print(' gracias por usar el software')
        
    if (opcion<1 or opcion>5):
        print('NO ES OPCION DISPONIBLE')

ejercicios resueltos Python 2eva_it2010_t3 pdf

ejercicios resueltos Matlab 2eva_it2010_t3 pdf

Ejercicio: 1Eva_IT2010_T2 Número Omirp

Propuesta de solución en Python: py_pdf, también en versión matlab: m_pdf

Nota: Omirp se lee de derecha a izquierda como primo.

Repasar algoritmo de validación de números primos, también el algoritmo para invertir dígitos de un número. En este ejercicio es necesario usar ambos.

Primero para verificar si el número a verificar es primo, luego para invertir sus dígitos y finalmente verificar si el número con dígitos invertidos también es primo.

Si ambos son primos entonces el número es omirp.

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2010_T2 Número Omirp
# Propuesta: edelros@espol.edu.ec

# INGRESO
n = int(input('numero a validar omirp: '))

# PROCEDIMIENTO

# revisa si es primo
esprimo = 1
i = 2
while (i<n):
    r = n%i
    if r==0:
        esprimo = 0
    i = i+1

# invierte los dígitos del número
m = n
alreves = 0
while (m>0):
    r = m%10
    m = m//10
    alreves = alreves*10 + r

# revisa si alreves es primo
esprimoA = 1
i = 2
while (i<alreves):
    r = alreves%i
    if r==0:
        esprimoA = 0
    i = i + 1

# revisa si es omirp
if (esprimo==1 and esprimoA==1):
    omirp = 1
else:
    omirp = 0

# SALIDA
print('es número omirp: ', omirp)

Resultado del algoritmo

numero a validar omirp: 1597
es número omirp:  1
>>> 
numero a validar omirp: 1598
es número omirp:  0
>>> 

---

Diagrama de Flujo

ejercicios resueltos Python 1eva_it2010_t2 pdf

ejercicios resueltos Matlab 1eva_it2010_t2 pdf

Ejercicio: 1Eva_IT2010_T1 Bono para televisores en Uruguay

Propuesta de solución en Python:

Para el bloque de ingreso de piden la cantidad de modelos, con lo que se puede crear la matriz con columnas cantidad y precio. Se usa una tercera columna para calcular el valor a devolver por cada modelo.

Ejemplo:

Modelo	Cantidad	Precio	Devolver
LCD	250	400	50.000
Plasma	120	1000	60.000
LED	80	3000	120.000
…	…	…	…

Total a Devolver: 230.000

Se suman los valores a devolver para presentar el resultado.

>>> 
¿cuántos modelos?: 3
modelo num: 0
cantidad:250
precio: 400
modelo num: 1
cantidad:120
precio: 1000
modelo num: 2
cantidad:80
precio: 3000
[[   250    400  50000      0]
 [   120   1000  60000      0]
 [    80   3000 120000      0]]
total a devolver:  230000
>>>

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2010_T1 Bono para televisores en Uruguay
# Tarea: convertir a listas
# Tarea: ingresar los nombres de los modelos

import numpy as np

# INGRESO
n = int(input('¿cuántos modelos?: '))

tabla  = np.zeros(shape=(n,3), dtype=int)
modelo = 0
while (modelo<n):
    print('modelo num:',modelo)
    tabla[modelo,0] = int(input('cantidad:' ))
    tabla[modelo,1] = int(input('precio: ' ))
    modelo = modelo + 1

# PROCEDIMIENTO
devolver = 0
modelo   = 0
while (modelo<n):
    tabla[modelo,2] = tabla[modelo,0]*tabla[modelo,1]/2
    devolver = devolver+tabla[modelo,2]
    modelo = modelo + 1

# SALIDA
print(tabla)
print('total a devolver: ',devolver)

Ejercicio: 2Eva_IIT2009_T3 Controlar saldos prepago

Propuesta de solución en Python: py_pdf, también en versión matlab: m_pdf

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 2Eva_IIT2009_T3 Controlar saldos prepago
# Propuesta: edelros@espol.edu.ec
# Registrar números de celular con listas

celular  = []
saldo    = []
mensajes = []

opcion = 0
while not(opcion==4):

    print('1. Ingresar equipo')
    print('2. Recargar saldo')
    print('3. transferir saldo')
    print('4. Salir')
    opcion = int(input('cual opcion: '))
    
    if (opcion==1):
        print('INGRESAR equipo')
        numero = input('numero celular:')
        celular.append(numero)
        saldo.append(0)
        mensajes.append(0)
        m = len(saldo)-1
        texto = str(celular[m])+' '+str(saldo[m])
        texto = texto +' '+str(mensajes[m])
        print(texto)

    elif (opcion==2):
        print('RECARGAR')
        numero   = input('numero celular: ')
        cantidad = input('    cantidad: ')

        # Busca el numero de celular
        m = len(saldo)
        encontre = -1
        i = 0
        while (i<m and encontre==-1):
            if (celular[i]==numero):
                encontre = i
            i = i + 1
            
        # si lo encuentra aumenta el saldo
        if (encontre>=0):
            saldo[encontre] = int(saldo[encontre]) + int(cantidad)
            print(encontre)
            texto = str(celular[encontre])+' '+str(saldo[encontre])
            texto = texto + ' ' + str(mensajes[encontre])
            print(texto)
        else:
            print('numero no registrado')
            
    elif (opcion==3):
        print('TRANSFERIR')
        donante  = input('numero donante : ')
        receptor = input('numero receptor: ')
        cantidad = input('       cantidad: ')

        # Busca el numero de celular donante
        m = len(saldo)
        encontreA = -1
        i = 0
        while (i<m and encontreA==-1):
            if (celular[i]==donante):
                encontreA = i
            i = i + 1
        # Busca el numero de celular receptor
        m = len(saldo)
        encontreB = -1
        i = 0
        while (i<m and encontreB==-1):
            if (celular[i]==receptor):
                encontreB = i
            i = i + 1
            
        #revisa condiciones para transferir
        condicion = encontreA>=0 and encontreB>=0 
        condicion = condicion and int(saldo[encontreA])>=int(cantidad)
        if condicion:
            saldo[encontreA] = int(saldo[encontreA])-int(cantidad)
            saldo[encontreB] = int(saldo[encontreB])+int(cantidad)
            print('saldo transferido: '+str(cantidad))
        else:
            if (encontreA==-1):
                print('no existe registro de donante:')
            if (encontreB==-1):
                print('no existe registro de receptor:')
        
    elif (opcion==4):
        print('Gracias por usar el software')
    else:
        print('opción no disponible..!')

resultado del algoritmo

1. Ingresar equipo
2. Recargar saldo
3. transferir saldo
4. Salir
cual opcion: 1
INGRESAR equipo
numero celular:987
987 0 0
1. Ingresar equipo
2. Recargar saldo
3. transferir saldo
4. Salir
cual opcion: 1
INGRESAR equipo
numero celular:876
876 0 0
1. Ingresar equipo
2. Recargar saldo
3. transferir saldo
4. Salir
cual opcion: 2
RECARGAR
numero celular: 987
    cantidad: 5
0
987 5 0
1. Ingresar equipo
2. Recargar saldo
3. transferir saldo
4. Salir
cual opcion: 2
RECARGAR
numero celular: 876
    cantidad: 1
1
876 1 0
1. Ingresar equipo
2. Recargar saldo
3. transferir saldo
4. Salir
cual opcion: 3
TRANSFERIR
numero donante : 987
numero receptor: 876
       cantidad: 3
saldo transferido: 3
1. Ingresar equipo
2. Recargar saldo
3. transferir saldo
4. Salir
cual opcion: 4
Gracias por usar el software
>>> 

ejercicios resueltos Python 2eva_iit2009_t3 pdf

ejercicios resueltos Matlab 2eva_iit2009_t3 pdf

Ejercicio: 2Eva_IIT2009_T2 Transponer una matriz

Se recorre toda la matriz intercambiando las posiciones de fila y columna. Lo mas sencillo es crear una nueva matriz de ceros con las dimensiones intercambiadas de la matriz inicial.

matriz = [[1,2,3],
          [4,5,6]]

Al recorrer las casillas de la matriz inicial en cada posición [f,c], se copian los valores en cada [c,f] de la nueva matriz. El resultado debería presentarse como:

[[1. 4.]
 [2. 5.]
 [3. 6.]]
>>>

Instrucciones en Python

# 2Eva_IIT2009_T2 Transponer una matriz
import numpy as np

def transponer(matriz):
    matriz = np.array(matriz)
    tamano = np.shape(matriz)
    n = tamano[0] # filas
    m = tamano[1] # columnas
    matrizT = np.zeros(shape=(m,n),dtype=float)
    for i in range(0,n,1):
        for j in range(0,m,1):
            matrizT[j,i] = matriz[i,j]
    return (matrizT)

# PROGRAMA EJEMPLO
# INICIO
matriz = [[1,2,3],
          [4,5,6]]

# PROCEDIMIENTO
matrizT = transponer(matriz)

# SALIDA
print(matrizT)

Nota: En Numpy existe la instrucción np.transpose(matriz) que realiza la misma operación. En el ejercicio se evalúa su comprensión e implementación del algoritmo, no se condidera que use las funciones de cada tópico de algebra en Python.

Ejercicio: 2Eva_IIT2009_T1 Mensaje a SMS

Propuesta de solución en Python:

Ejemplo, solo para 'de'-'d':
>>> mensaje='un estudiante de la espol que estudia'
>>> txtsms(mensaje)
'un estudiante d la espol que estudia'

El nuevo mensaje se realiza copiando el mensaje letra por letra y analizando cada una para revisar si aplica la regla de sms.

Para el ejemplo solo para la letra ‘d’, se revisa las letras anteriores y posteriores para estimar que se puede saltar la copia de la letra.

considere que para el análisis planteado i tiene que ser mayor que 1, sino se mostrará error al no tener suficientes letras previas

>>> mensaje='de su mensaje sms'
>>> txtsms(mensaje)
'de su mensaje sms'

implemente el caso presentado en el algoritmo presentado a continuación:

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 2Eva_IIT2009_T1 Mensaje a SMS
# TAREA: completarotras opciones: que,se,lo

def txtsms(mensaje):
    tm=len(mensaje)
    
    # inicializa variable de salida
    sms = ''
    i = 0
    while not(i>=(tm)):
        
        # si encuentra una 'd' se salta un espacio
        if (mensaje[i-1]=='d' and mensaje[i-2]==' '
            and mensaje[i+1]==' '):
            i = i + 1
            
        # copia un caracter
        sms = sms + mensaje[i]
        i = i + 1
        
    return(sms)