Categoría: Solución 1ra Evaluación

Ejercicio: 1Eva_IT2011_T2 Subasta Inversa

Solución propuesta en Archivo matlab en pdf

Propuesta de Solución: Solicitar los datos de las ofertas por vendedor en un vector oferta(i).

Use el “algoritmo del menor” para determinar al vendedor con menor valor de oferta.

Identificado el vendedor menor, contar cuántos igualan la mejor oferta.

Si el contador es mayor que 1, sortear entre los vendedores hasta que el sorteo recaiga en un vendedor que si cumpla.

Mostrar los resultados

Tarea: convertir a instrucciones Python el siguiente diagrama de flujo:

 

 

ejercicios resueltos Matlab 1eva_it2011_t2 pdf

Ejercicio: 1Eva_IT2011_T1 Ahorros de Juan vs Pedro

Propuesta de solución en Python: py_pdf, también en versión matlab: py_pdf

Ingresar los datos para cada depositante en variables separadas.

Luego, calcular por cada año los saldos para cada depositante, repitiendo hasta que se cumpla la condición que Juan tenga más dinero que Pedro.

La variable “año” es un contador simple que inicia en cero, en finanzas significa el momento en que se deposita.

Cuando termina el año completo se considera incrementado en 1.

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2011_T1 Ahorros de Juan vs Pedro
# Propuesta: edelros@espol.edu.ec

# INGRESO
ca = float(input('Banco A - Capital Inicial:   '))
ra = float(input('Banco A - Tasa Interés Anual:'))
cb = float(input('Banco B - Capital Inicial:   '))
rb = float(input('Banco B - Tasa Interés Anual:'))

# PROCEDIMIENTO
anio = 0
sa = ca
sb = cb

while (sa<=sb):
    anio = anio + 1
    sa   = ca*((1+ra)**anio)
    sb   = cb*((1+rb)**anio)

# SALIDA
print('años transcurridos: ', anio)

Resultado del algoritmo

Banco A - Capital Inicial:   100
Banco A - Tasa Interés Anual:0.065
Banco B - Capital Inicial:   120
Banco B - Tasa Interés Anual:0.055
años transcurridos:  20
>>> 
Banco A - Capital Inicial:   100
Banco A - Tasa Interés Anual:0.067
Banco B - Capital Inicial:   120
Banco B - Tasa Interés Anual:0.055
años transcurridos:  17
>>> 

---

Diagrama de Flujo Mientras-Repita

Diagrama de Flujo Repita-Hasta

ejercicios resueltos Python 1eva_it2011_t1 pdf

ejercicios resueltos Matlab 1eva_it2011_t1 pdf

 

Ejercicio: 1Eva_IIT2010_T3 Juego del amigo secreto

Propuesta de solución en Python: py_pdf, tambien en matlab: m_pdf

Inicie el sorteo con banderas de amigo/amiga en cero,

AmigA = np.zeros(n+1,dtype=int)
AmigO = np.zeros(2*n+1,dtype=int)

para poner luego el valor sorteado a cada uno, si aún no se ha repetido.

dama = int(rnd.random()*n)+(n+1)

El valor repetido se verifica revisando el estado del arreglo en la posición correspondiente, esperando que sea vacio AmigO[dama]==0, solo allí se asigna el amigo y se pasa al siguiente sorteo.

# sortea dama para cada AmigO
i = 1
while (i<=n):
    dama = int(rnd.random()*n)+(n+1)
    if (AmigO[dama]==0):
        AmigO[dama] = i
        i = i+1

ser repite el mismo proceso para el otro género.

---

Instrucciones en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2010_T3 Juego del amigo secreto
# Propuesta de solucion. edelros@espol.edu.ec

import numpy as np
import random as rnd

# INGRESO
n = int(input('¿número de parejas?: '))

# PROCEDIMIENTO
AmigA = np.zeros(n+1,dtype=int)
AmigO = np.zeros(2*n+1,dtype=int)

# sortea dama para cada AmigO
i = 1
while (i<=n):
    dama = int(rnd.random()*n)+(n+1)
    if (AmigO[dama]==0):
        AmigO[dama] = i
        i = i+1

# sortea caballero para cada AmigA
j = n+1
while (j<=(2*n)):
    caballero = int(rnd.random()*n)+1
    if (AmigA[caballero]==0):
        AmigA[caballero] = j
        j = j+1

# SALIDA
print('pareja de caballeros')
i = 1
while (i<=n):
    print(i,' , ',AmigA[i])
    i = i+1
    
print('pareja de damas')
j = n+1
while (j<=(2*n)):
    print(j,' , ',AmigO[j])
    j = j+1

Resultado del algoritmo

¿número de parejas?: 4
pareja de caballeros
1  ,  5
2  ,  8
3  ,  7
4  ,  6
pareja de damas
5  ,  3
6  ,  4
7  ,  1
8  ,  2
>>> 

---

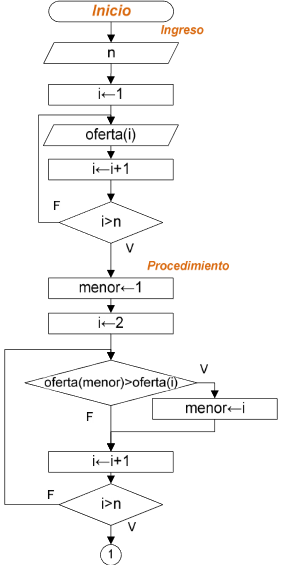
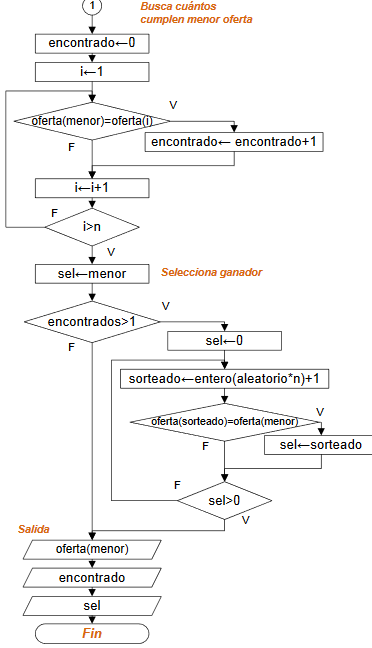
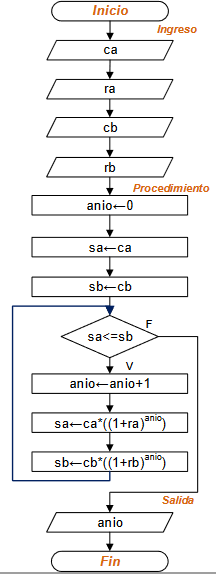
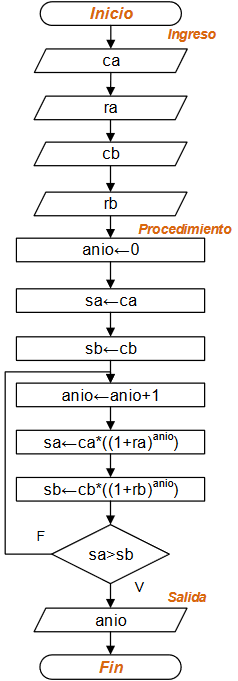
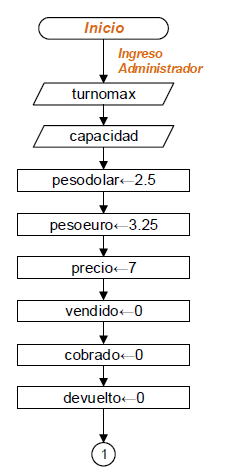
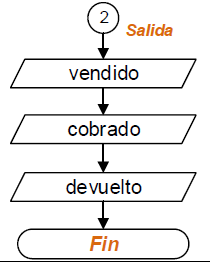
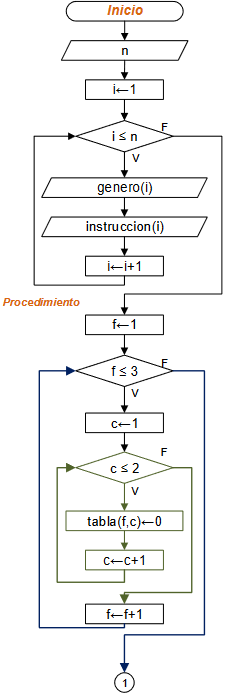
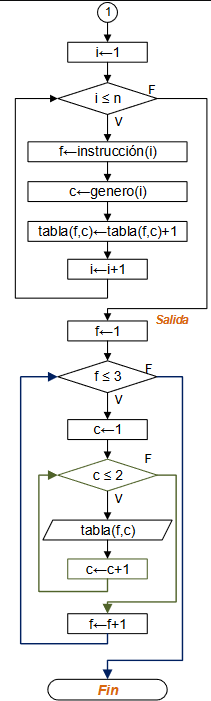
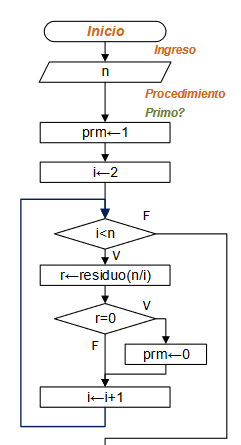
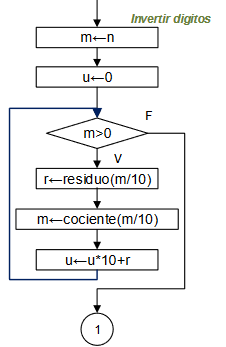
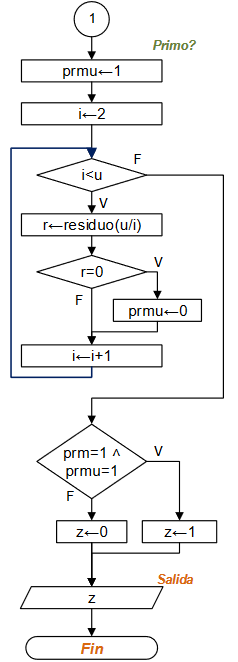
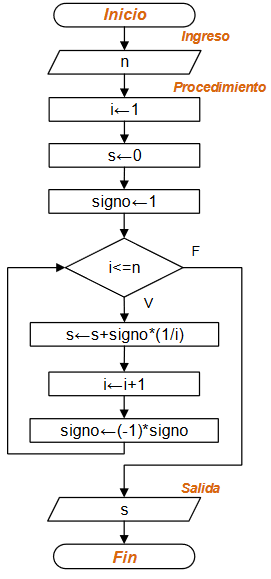
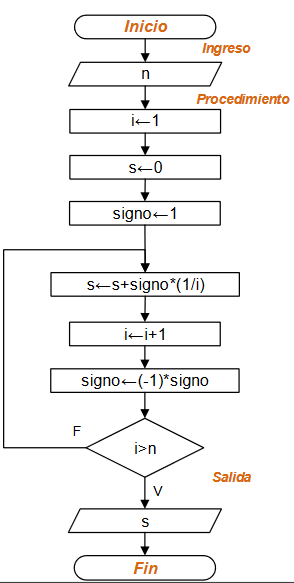
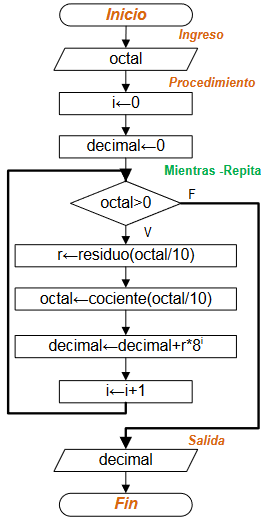
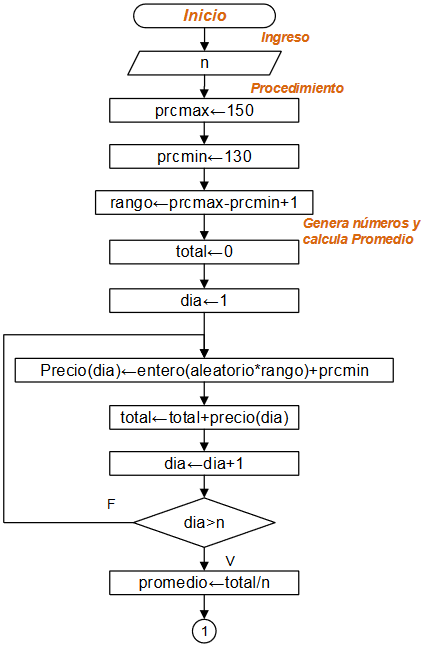
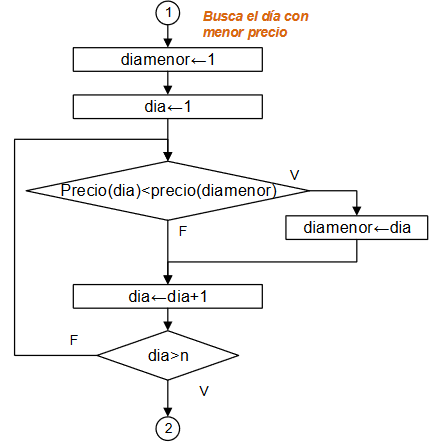
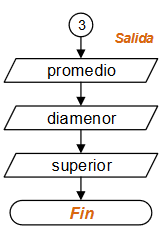
Diagrama de Flujo

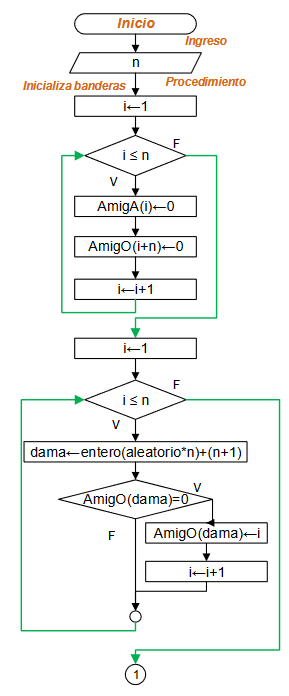
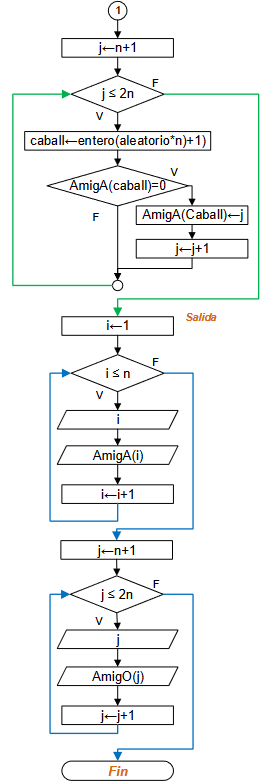
ejercicios resueltos Python 1eva_iit2010_t3 pdf

ejercicios resueltos Matlab 1eva_iit2010_t3 pdf

Ejercicio: 1Eva_IIT2010_T2 Venta de pasajes tren turístico

Solución propuesta:  py_pdf, versión matlab m_pdf

Inicialmente desarrolle la venta para un solo pedido/comprador, así encontrará las partes principales de la venta y hace el primer esquema del procedimiento a seguir.

pedido = int(input('¿cuántos pasajes?: '))
print('   Monedas: 1.Dolar 2.Euro 3.Peso')
moneda = int(input(' ¿Tipo Moneda?: '))
cantidad = float(input(' ¿Cantidad de Dinero?: '))

if (moneda==1):
    valor = cantidad*pesodolar
if (moneda==2):
    valor = cantidad*pesoeuro
if (moneda==3):
    valor = cantidad

pago=pedido*precio

En una segunda versión, agregue las demás opciones de control, tales como contadores y acumuladores para controlarlos turnos o la venta de asientos del tren.

En este proceso se añade un lazo para repetir, y se termina mostrando los resultados de boletos vendidos, el dinero cobrado y el total devuelto.

Tarea: Prestar atención en la venta cuando quedan pocos boletos y el usuario quiere comprar más de los que están disponibles

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2010_T1 Venta de pasajes tren turístico
# Propuesta: edelros@espol.edu.ec

turnomax = int(input('¿cuántos turnos?: '))
capacidad = int(input('capacidad del tren?: ')) 

pesodolar = 2.50
pesoeuro  = 3.25
precio    = 7.00
vendido   = 0
cobrado   = 0.00
devuelto  = 0.00

turno = 1
while (turno<=turnomax and vendido<=capacidad):
    print('Turno:')
    print(turno)
    pedido = int(input('¿cuántos pasajes?: '))
    print('   Monedas: 1.Dolar 2.Euro 3.Peso')
    moneda = int(input(' ¿Tipo Moneda?: '))
    cantidad = float(input(' ¿Cantidad de Dinero?: '))

    if (moneda==1):
        valor = cantidad*pesodolar
    if (moneda==2):
        valor = cantidad*pesoeuro
    if (moneda==3):
        valor = cantidad

    pago=pedido*precio
    if (pago<=valor and((vendido+pedido)<capacidad)):
        vendido = vendido+pedido
        cobrado = cobrado+pago
        cambio  = valor-pago
        devuelto = devuelto+cambio

        print('Se vendieron Boletos: ')
        print(pedido)
        print('su cambio: ')
        print(cambio)
    else:
        print('no es dinero suficiente')

    turno = turno + 1

# SALIDA
print('pasajes vendidos: ')
print(vendido)
print('pesos cobrados: ')
print(cobrado)
print('pesos devueltos: ')
print(devuelto)

Resultado del algoritmo

¿cuántos turnos?: 3
capacidad del tren?: 50
Turno:
1
¿cuántos pasajes?: 3
   Monedas: 1.Dolar 2.Euro 3.Peso
 ¿Tipo Moneda?: 1
 ¿Cantidad de Dinero?: 20
Se vendieron Boletos: 
3
su cambio: 
29.0
Turno:
2
¿cuántos pasajes?: 4
   Monedas: 1.Dolar 2.Euro 3.Peso
 ¿Tipo Moneda?: 2
 ¿Cantidad de Dinero?: 20
Se vendieron Boletos: 
4
su cambio: 
37.0
Turno:
3
¿cuántos pasajes?: 2
   Monedas: 1.Dolar 2.Euro 3.Peso
 ¿Tipo Moneda?: 3
 ¿Cantidad de Dinero?: 30
Se vendieron Boletos: 
2
su cambio: 
16.0
pasajes vendidos: 
9
pesos cobrados: 
63.0
pesos devueltos: 
82.0
>>> 

Diagrama de Flujo

 

 

ejercicios resueltos Python 1eva_iit2010_t2 pdf ejercicios resueltos Matlab 1eva_iit2010_t2 pdf

Ejercicio: 1Eva_IIT2010_T1 Censo de instrucción por género

Propuesta de solución en Python: py_pdf, también en matlab: m_pdf

Los datos se almacenan en vectores y se los tabula/cuenta en una matriz.  Las filas representan la instrucción y columna el género.

Lista de género y nivel de instrucción:

i	Género [i]	Instrucción [i]	Género: 1. Masculino 2. FemeninoInstrucción: 1. Primaria 2. Secundaria 3. Superior
1	1	2
2	2	3
3	1	3
…	…	…
n	…	…

Se usará desde la casilla 1, por lo que el tamaño del arreglo es n+1 al no usar la casilla cero.

n = int(input('¿Cuántos formularios: '))

genero = np.zeros(n+1,dtype=int)
instruccion = np.zeros(n+1,dtype=int)
i = 1
while not(i>n):
    print('Formulario:',i)
    genero[i] = int(input('  genero: '))
    instruccion[i] = int(input('  instruccion: '))
    i = i+1

Se inicializan los contadores al inicializar la matriz para luego procesar los datos de todos los formularios registrados.

Instrucción por género:

	Masculino	Femenino
Primaria
Secundaria
Superior

Para facilitar la lectura del algoritmo se usan como variables f y c para referenciar las filas y columnas. Una forma más larga de solución podría usar contadores individuales para contar primaria/masculino, primaria/femenino, etc.

Tarea: validar el ingreso de género e instrucción por cada formulario

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2010_T1 Censo de instrucción por género
# propuesta: edelros@espol.edu.ec

import numpy as np

#INGRESO
n = int(input('¿Cuántos formularios: '))

genero = np.zeros(n+1,dtype=int)
instruccion = np.zeros(n+1,dtype=int)

i = 1
while not(i>n):
    print('Formulario:',i)
    genero[i] = int(input('  genero: '))
    instruccion[i] = int(input('  instruccion: '))
    i = i+1

# PROCEDIMIENTO
tabla = np.zeros(shape=(3+1,2+1),dtype=int)
i = 1
while not(i>n):
    f = instruccion[i]
    c = genero[i]
    tabla[f,c] = tabla[f,c]+1
    i = i + 1

# SALIDA
print('Instr  M  F ')
f = 1
while not(f>3):
    c = 1
    cadena = ''
    while not(c>2):
        cadena = cadena+' '+str(tabla[f,c])
        c = c + 1
    print('   '+str(f)+': '+cadena)
    f = f + 1

Resultado del algoritmo

¿Cuántos formularios: 5
Formulario: 1
  genero: 1
  instruccion: 2
Formulario: 2
  genero: 1
  instruccion: 2
Formulario: 3
  genero: 2
  instruccion: 1
Formulario: 4
  genero: 2
  instruccion: 1
Formulario: 5
  genero: 2
  instruccion: 3
Instr  M  F 
   1:  0 2
   2:  2 0
   3:  0 1
>>> 

---

Diagrama Flujo Mientras-Repita

ejercicios resueltos Python 1eva_iit2010_t1 pdf

ejercicios resueltos Matlab 1eva_iit2010_t1 pdf

Ejercicio: 1Eva_IT2010_T2 Número Omirp

Propuesta de solución en Python: py_pdf, también en versión matlab: m_pdf

Nota: Omirp se lee de derecha a izquierda como primo.

Repasar algoritmo de validación de números primos, también el algoritmo para invertir dígitos de un número. En este ejercicio es necesario usar ambos.

Primero para verificar si el número a verificar es primo, luego para invertir sus dígitos y finalmente verificar si el número con dígitos invertidos también es primo.

Si ambos son primos entonces el número es omirp.

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2010_T2 Número Omirp
# Propuesta: edelros@espol.edu.ec

# INGRESO
n = int(input('numero a validar omirp: '))

# PROCEDIMIENTO

# revisa si es primo
esprimo = 1
i = 2
while (i<n):
    r = n%i
    if r==0:
        esprimo = 0
    i = i+1

# invierte los dígitos del número
m = n
alreves = 0
while (m>0):
    r = m%10
    m = m//10
    alreves = alreves*10 + r

# revisa si alreves es primo
esprimoA = 1
i = 2
while (i<alreves):
    r = alreves%i
    if r==0:
        esprimoA = 0
    i = i + 1

# revisa si es omirp
if (esprimo==1 and esprimoA==1):
    omirp = 1
else:
    omirp = 0

# SALIDA
print('es número omirp: ', omirp)

Resultado del algoritmo

numero a validar omirp: 1597
es número omirp:  1
>>> 
numero a validar omirp: 1598
es número omirp:  0
>>> 

---

Diagrama de Flujo

ejercicios resueltos Python 1eva_it2010_t2 pdf

ejercicios resueltos Matlab 1eva_it2010_t2 pdf

Ejercicio: 1Eva_IT2010_T1 Bono para televisores en Uruguay

Propuesta de solución en Python:

Para el bloque de ingreso de piden la cantidad de modelos, con lo que se puede crear la matriz con columnas cantidad y precio. Se usa una tercera columna para calcular el valor a devolver por cada modelo.

Ejemplo:

Modelo	Cantidad	Precio	Devolver
LCD	250	400	50.000
Plasma	120	1000	60.000
LED	80	3000	120.000
…	…	…	…

Total a Devolver: 230.000

Se suman los valores a devolver para presentar el resultado.

>>> 
¿cuántos modelos?: 3
modelo num: 0
cantidad:250
precio: 400
modelo num: 1
cantidad:120
precio: 1000
modelo num: 2
cantidad:80
precio: 3000
[[   250    400  50000      0]
 [   120   1000  60000      0]
 [    80   3000 120000      0]]
total a devolver:  230000
>>>

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2010_T1 Bono para televisores en Uruguay
# Tarea: convertir a listas
# Tarea: ingresar los nombres de los modelos

import numpy as np

# INGRESO
n = int(input('¿cuántos modelos?: '))

tabla  = np.zeros(shape=(n,3), dtype=int)
modelo = 0
while (modelo<n):
    print('modelo num:',modelo)
    tabla[modelo,0] = int(input('cantidad:' ))
    tabla[modelo,1] = int(input('precio: ' ))
    modelo = modelo + 1

# PROCEDIMIENTO
devolver = 0
modelo   = 0
while (modelo<n):
    tabla[modelo,2] = tabla[modelo,0]*tabla[modelo,1]/2
    devolver = devolver+tabla[modelo,2]
    modelo = modelo + 1

# SALIDA
print(tabla)
print('total a devolver: ',devolver)

Ejercicio: 1Eva_IT2009_T1 Suma de serie con signo alternado

Propuesta de solución en Python: python.pdf, también versión en matlab.pdf

Solicitar el número n, calcular cada término i-ésimos y acumularlos en una variable s.

El signo se puede alternar multiplicando una variable signo por -1. También se puede usar (-1)ⁱ⁺¹ para alternar el signo.

1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}+\text{...}+\frac{1}{n}

observe:

(-1)^{(1+1)}1+(-1)^{(2+1)}\frac{1}{2}+(-1)^{(3+1)}\frac{1}{3}+ ...

La primera solución se presenta usando el lazo “Mientras-Repita”

Lazo mientras-repita:

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2009_T1 Suma de serie con signo alternado
# Propuesta de solución. edelros@espol.edu.ec

# INGRESO
n = int(input('¿Cuántos términos?: '))

# PROCEDIMIENTO
i = 1
s = 0
signo = 1
while (i<=n):
    s = s + signo*(1/i)
    i = i + 1
    signo = (-1)*signo

# SALIDA
print(s)

resultado del algoritmo

¿Cuántos términos?: 5
0.7833333333333332
>>> 
== RESTART: D:\MATG1052Ejemplos\unprograma.py ==
¿Cuántos términos?: 10
0.6456349206349207
>>> 

Diagrama de Flujo Mientras-Repita

---

lazo repita-hasta:

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2009_T1 Suma de serie con signo alternado
# Propuesta de solución. edelros@espol.edu.ec

# INGRESO
n = int(input('¿Cuántos términos?: '))

# PROCEDIMIENTO
i = 1
s = 0
signo = 1
while not(i>n):
    s = s + signo*(1/i)
    i = i + 1
    signo = (-1)*signo

# SALIDA
print(s)

Diagrama de Flujo Repita-Hasta

ejercicios resueltos Python 1Eva_IT2009_T1 pdf

ejercicios resueltos Matlab 1eva_it2009_t1 pdf

Ejercicio: 1Eva_IIT2008_T1 Odómetro OCTAL

Propuesta de solución en Python: py_pdf, también en matlab: m_pdf

Se usa el concepto para cambio de base numérica, se extrae cada dígito para acumular el valor ponderando por cada posición referenciada con la variable i.

Si se usa residuo de la división para 10, el primer dígito a extraer es el menos significativo (unidades).

Se acumulan los valores de acuerdo a la ponderación o peso por posición y se repite hasta que no queden dígitos que ponderar.

Para repasar: Bases Numéricas Introducción

Tarea: validar que el número es octal (rango de dígitos entre 0-7)-

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2008_T1 Odometro OCTAL
# Propuesta de solución. edelros@espol.edu.ec
# Tarea: Validar que el ingreso sea en octal.

# INGRESO
octal = int(input('¿numero en octal?: '))

# PROCEDIMIENTO
i = 0
decimal = 0
while (octal>0):
    r = octal%10
    octal = octal//10
    decimal = decimal+r*(8**i)
    i = i + 1

# SALIDA
print('valor en decimal: ')
print(decimal)

Resultado del algoritmo

Observación: Tener en cuenta que no se ha validado que el número octal solo debe tener dígitos entre 0 y 7.

¿numero en octal?: 27
valor en decimal: 
23
>>> 
¿numero en octal?: 14
valor en decimal: 
12
>>> 

Diagrama de Flujo

ejercicios resueltos Python 1eva_iit2008_t1 pdf

ejercicios resueltos Matlab 1eva_iit2008_t1 pdf

Ejercicio: 1Eva_IT2008_T3 Simular Precio del Petróleo

Propuesta de solución en Python: py_pdf 

También como diagrama en pdf y en versión matlab: m_pdf

Se ingresa la cantidad de días del mes, o se puede considerar directamente 30, también es opcional ingresar el rango de precio mínimo y precio máximo, que son los límites del número aleatorio.

Para la pregunta a) se calcula el promedio como el acumulado de precios de cada día dividido para los n días.

Enla pregunta b) se usa el algoritmo del menor, con la hipótesis que el díamenor es el primero, y que el precio menor es el máximo posible, a fin que se reemplace con el primer menor encontrado.

Se deja la pregunta c) como tarea a fin de que se desarrolle el problema usando un arreglo.

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2008_T3 Simular Precio del Petróleo
# Propuesta: edelros@espol.edu.ec
# Tarea: Realizar el literal c)

import random as rnd

# INGRESO
n = int(input('días del mes: '))

# PROCEDIMIENTO
prcmax = 150
prcmin = 130
rango  = prcmax-prcmin+1
diamenor = 1
pmenor = prcmax

dia = 1
total = 0
while (dia<=n):
    precio = int(rnd.random()*rango)+prcmin
    total  = total+precio

    if (precio<pmenor):
        diamenor = dia
        pmenor   = precio

    dia = dia+1

promedio = total/n

# SALIDA
print('promedio: ')
print(promedio)
print('día de menor precio:')
print(diamenor)

---

Versión Usando Arreglos:

Propuesta de solución Python: py_pdf, también en versión matlab: m_pdf

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2008_T3 Simular Precio del Petróleo
# Tema 3. Precio petroleo-Arreglo
# Propuesta: edelros@espol.edu.ec

import random as rnd
import numpy as np

# INGRESO
n = int(input('días del mes: '))

# PROCEDIMIENTO
prcmax = 150
prcmin = 130
rango  = prcmax-prcmin+1
precio = np.zeros((n+1),dtype=int)

# algoritmo del promedio
total = 0
dia   = 1
while (dia<=n):
    precio[dia] = int(rnd.random()*rango)+prcmin
    total = total + precio[dia]
    dia   = dia + 1

promedio = total/n

# algoritmo del menor
diamenor = 1
dia = 1
while (dia<=n):
    if precio[dia]<precio[diamenor]:
        diamenor = dia
    dia = dia + 1

# algoritmo precio superior al promedio
superior = 0
dia = 1
while (dia<=n):
    if precio[dia]>promedio:
        superior = superior + 1
    dia = dia + 1

# SALIDA
print('promedio: ')
print(promedio)
print('día de menor precio:')
print(diamenor)
print('días con precio sobre promedio:')
print(superior)

Resultado del algoritmo

días del mes: 30
promedio: 
140.06666666666666
día de menor precio:
14
días con precio sobre promedio:
16
>>> 

---

Diagrama de Flujo

ejercicios resueltos Python 1eva_it2008_t3 pdf

ejercicios resueltos Python 1eva_it2008_t3_flujo pdf

ejercicios resueltos Matlab 1eva_it2008_t3 pdf