5.2 Optica – Rayo reflejado en plano inclinado con Python
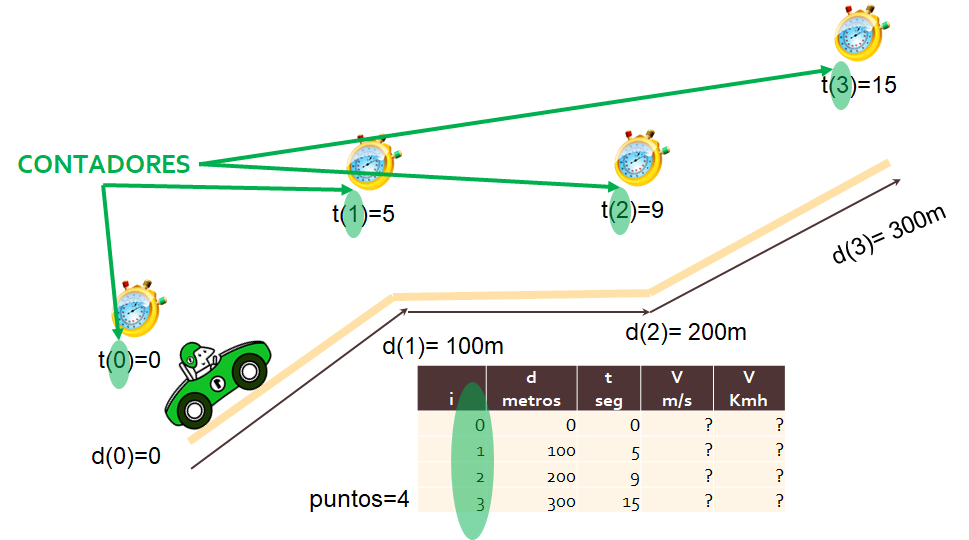
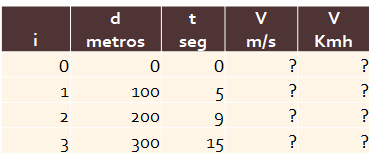
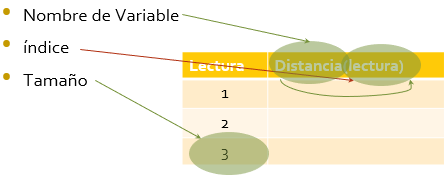
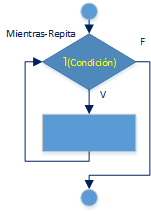
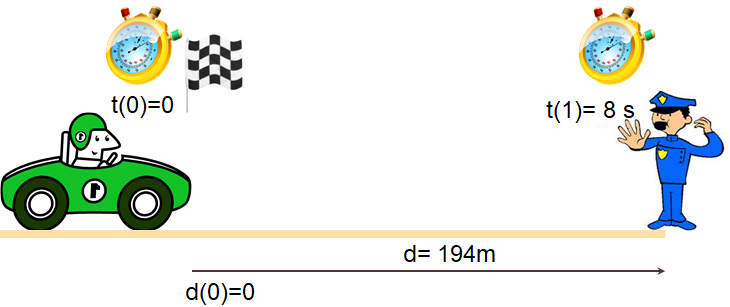
Propagación multitrayecto o multicamino en plano inclinado
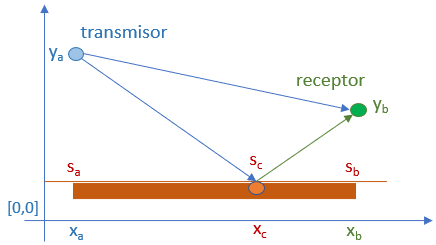
Referencia: Sears-Zemansky Cap33.2 Vol2 Ed.12 p1123, Optica – Rayo reflejado en plano horizontal
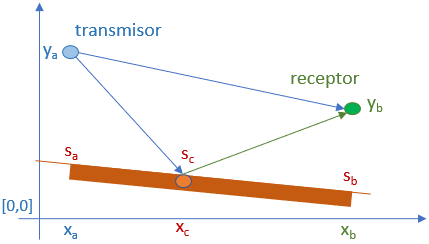
El plano de reflexión puede estar inclinado respecto al eje de las x. Para el caso dado, se puede considerar igualar las pendientes del rayo incidente y reflejado referenciadas con la pendiente del plano inclinado.
la pendiente del plano inclinado se obtiene como:
m_s = \frac{\Delta suelo } {\Delta x_{intervalo}} = \frac{s_b-s_a}{x_b-x_a}Respecto al plano, los ángulos de rayo incidente y reflejado son iguales por lo que secorrige con la pendiente del plano. Las pendientes del rayo izquierdo y rayo derecho con la influencia de la pendiente del suelo se igualan:
-(m_z-m_s) = m_r-m_s -m_z = m_r - 2 m_sPara obtener sc como un punto en el plano, requiere función de suelo(x) evaluada en sc , para usar todo en función de xc :
m_s = \frac{\Delta s}{\Delta x} = \frac{s_b-s_a}{x_b-x_a} s(x) = m_s x_a +b_s b_s = s_a-m_s x_a s_c = s(c) = m_s x_c +b_sLo anterior permite actualizar el planteamiento de la pendientes, y despejar el valor de la incógnita xc
-m_z = m_r - 2 m_s - \frac{s_c-y_a}{x_c-x_a} = \frac{y_b-s_c}{x_b-x_c}-2m_s - \frac{s_c-y_a}{x_c-x_a} = \frac{y_b-s_c-2m_s(x_b-x_c)}{x_b-x_c}primero se busca agrupar sc
-(x_b-x_c)(s_c-y_a) = (x_c-x_a)(y_b-s_c-2m_s(x_b-x_c))-s_c(x_b-x_c)+y_a(x_b-x_c) = y_b(x_c-x_a)-s_c(x_c-x_a)-2m_s(x_b-x_c)(x_c-x_a)
-s_c(x_b-x_c) + s_c(x_c-x_a) = -y_a(x_b-x_c) + y_b(x_c-x_a) - 2m_s(x_b-x_c)(x_c-x_a)
s_c(-x_b+x_c+x_c-x_a) = -x_b y_a+x_c y_a + y_b x_c - x_a y_b -2m_s(x_b(x_c-x_a)-x_c(x_c-x_a))
sutituyendo sc con la expresión del plano con pendiente evaluada en el punto xc , lo que se expresa como:
(m_s x_c +b_s)(2 x_c-(x_a+x_b)) = x_c (y_a + y_b)-(x_a y_b -x_b y_a)-2m_s(x_b x_c- x_a x_b - x_c^2 + x_a x_c))teniendo ahora como objetivo encontrar una expresión para xc
m_s x_c (2 x_c-(x_a+x_b))+b_s(2 x_c-(x_a+x_b)) = x_c (y_a + y_b)-(x_a y_b +x_b y_a)-2m_s(- x_c^2 + x_c(x_b + x_a) - x_a x_b)2m_s x_c^2 - m_s x_c(x_a+x_b)+2 b_s x_c-b_s(x_a+x_b) = x_c (y_a + y_b)-(x_a y_b +x_b y_a)+ 2m_s x_c^2 - 2m_s x_c (x_b + x_a) + 2m_s x_a x_b
x_c(- m_s (x_a+x_b)+2 b_s)-b_s(x_a+x_b) = x_c (y_a + y_b- 2m_s (x_b + x_a))-(x_a y_b +x_b y_a) + 2m_s x_a x_b
x_c(- m_s (x_a+x_b)+2 b_s) -x_c (y_a + y_b- 2m_s (x_b + x_a)) = b_s(x_a+x_b) -(x_a y_b +x_b y_a) + 2m_s x_a x_b
x_c(2 b_s - (y_a + y_b) - m_s (x_a+x_b) + 2m_s (x_b + x_a)) = b_s(x_a+x_b) -(x_a y_b +x_b y_a) + 2m_s x_a x_b
x_c(2 b_s - (y_a + y_b) + m_s(x_a+x_b) = b_s(x_a+x_b) -(x_a y_b +x_b y_a) + 2m_s x_a x_b
x_c(2 b_s - (y_a + y_b) + m_s (x_a+x_b)) = b_s(x_a+x_b) -(x_a y_b +x_b y_a) + 2m_s x_a x_b
x_c = \frac{b_s(x_a+x_b) -(x_a y_b +x_b y_a) + 2m_s x_a x_b}{2 b_s - (y_a + y_b) + m_s (x_a+x_b)}
Con el valor de xc se pudede obtener la altura del punto sc. a partir de la ecuación que describe el plano s(x).
Algoritmo en Python
A partir del algoritmo del rayo reflejado en plano horizontal , se añaden las instrucciones para calcular ms, bs, xc, sc.
obteniendo ahora el resultado:
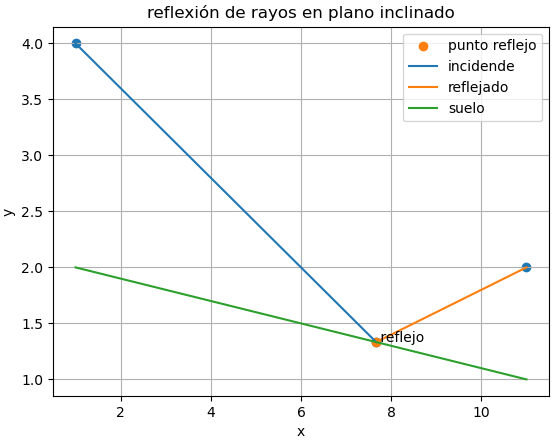
punto reflejado: [ 7.666666666666665 , 1.3333333333333335 ]
con la gráfica
Instrucciones en Python
# rayo incidente y reflejado # en plano inclinado # blog.espol.edu.ec/ccpg1001 import numpy as np import matplotlib.pyplot as plt # INGRESO # posición de antenas xa = 1 # Izquierda ya = 4 xb = 11 # Derecha yb = 2 # plano el suelo sa = 2 sb = 1 # muestras en grafica muestras = 21 # PROCEDIMIENTO # pendiente de suelo ms = (sb-sa)/(xb-xa) bs = sa-ms*xa # punto de reflejo numerador = bs*(xa+xb)-(xa*yb+xb*ya)+2*ms*xa*xb denominador = 2*bs-(ya+yb)+ms*(xa+xb) xc = numerador/denominador sc = ms*xc+bs # SALIDA print('punto reflejado: [',xc,',',sc,']') # GRAFICA #puntos en el plano plt.scatter([xa,xc,xb],[ya,sc,yb]) plt.scatter([xc],[sc],label='punto reflejo') # lineas de rayos plt.plot([xa,xc],[ya,sc],label='incidende') plt.plot([xc,xb],[sc,yb],label='reflejado') plt.plot([xa,xb],[sa,sb],label='suelo') # etiquetas anotadas plt.annotate(' reflejo',[xc,sc]) # etiquetas plt.legend() plt.xlabel('x') plt.ylabel('y') plt.title('reflexión de rayos en plano inclinado') plt.grid() plt.show()
Tarea: Consiere que el suelo está compuesto de al menos dos segmentos con inclinaciones diferentes. Podría darse mas de una reflexión al punto de recepción o ninguna
Una aplicación relacionada de análisis multitrayecto en Girni: Coordenadas – Rayo reflejado en perfil por tramos
5.1 Optica – Rayo reflejado en plano horizontal con Python
Referencia: Sears-Zemansky Cap33.2 Vol2 Ed.12 p1123
El modelo de luz basado en rayos permite describir la propagación por: reflexión y refracción.
Un rayo de onda luminosa que incide en una material liso que separa dos materiales transparentes (como el aire y el vidrio o el agua y el vidrio), el rayo es reflejado parcialmente y también refractado parcialmente hacia el segundo material.
Los rayos incidente, reflejado y refractado en una interfaz lisa entre dos materiales ópticos forman ángulos θa,θr,θb respecto a la normal (perpendicular) a la superficie en el punto de incidencia se ilustra en la figura. Si la superficie es rugosa, tanto la luz transmitida como la reflejada se dispersan en varias direcciones y no hay un ángulo único de transmisión o reflexión.
La reflexión con un ángulo definido desde una superficie muy lisa se llama reflexión especular ( latin de “espejo”). La reflexión dispersa a partir de una superficie áspera se llama reflexión difusa.
Propagación multitrayecto o multicamino en plano horizontal
Referencia: Propagación multicamino
En telecomunicaciones, la propagación de ondas de radio presentan un comportamiento semejante al de la luz para reflexión conocido como propagación multicamino o multitrayecto.
El fenómeno se da cuando las señales de radio llegan a la antena receptora por dos o más caminos y en diferentes tiempos.
La propagación mutitrayecto puede causar problemas en la recepción de la señal, debido a la interacción entre las señales recibidas. A fines prácticos, la señal obtenida en recepción difiere de la original y causa efectos que se han de compensar.
Ejercicio con gráfica
Realizar la gráfica de los rayos incidente, reflejado y directo entre el transmisor y receptor con antenas a diferentes alturas, semejante a la gráfica anterior.
Desarrollo
Si los ángulos incidente y reflejado son iguales, la pendiente rayo incidente debe ser igual en magnitud a la pendiente del rayo reflejado. Las pendientes tienen signo opuesto, el rayo izquierdo tiene pendiente negativa.
- \frac{\Delta y_{izquierda}} {\Delta x_{izquierda}} = \frac{\Delta y_{derecha}}{\Delta x_{derecha}} - \frac{s_c-y_a}{x_c-x_a} = \frac{y_b-s_c}{x_b-x_c}Por facilidad de la ecuación, se supondrá que el suelo es paralelo al eje x, a una altura sc del eje de referencia.
Se debe obtener el valor de xc de la ecuación anterior, que realizando un poco de trabajo se obtiene que:
- (x_b-x_c)(s_c-y_a) = (x_c-x_a)(y_b-s_c) - x_b(s_c-y_a) + x_c (s_c-y_a) = x_c (y_b-s_c)-x_a (y_b-s_c) x_c (s_c-y_a) - x_c (y_b-s_c)= -x_a (y_b-s_c) + x_b(s_c-y_a) x_c (2s_c-y_a-y_b)= -x_a (y_b-s_c) + x_b(s_c-y_a) x_c = \frac{x_b(s_c-y_a)-x_a(y_b-s_c)}{2s_c-y_a-y_b}Obtenido el punto xc y dado que el plano es horizontal, la altura sc es constante.
Con el algoritmo se puede obtener el punto de reflexión para varias alturas de antena y varias alturas del plano.
resultado con datos muestra:
punto reflejado: [ 8.5 , 1 ]
Instrucciones en Python
# rayo incidente y reflejado # blog.espol.edu.ec/ccpg1001 import numpy as np import matplotlib.pyplot as plt # INGRESO # posición de antenas xa = 1 # Izquierda ya = 4 xb = 11 # Derecha yb = 2 # plano el suelo sc = 1 # altura # muestras en grafica muestras = 21 # PROCEDIMIENTO numerador = xb*(sc-ya)-xa*(yb-sc) denominador = 2*sc-ya-yb xc = numerador/denominador # SALIDA print('punto reflejado: [',xc,',',sc,']') # GRAFICA #puntos en el plano plt.scatter([xa,xc,xb],[ya,sc,yb]) plt.scatter([xc],[sc],label='punto reflejo') # lineas de rayos plt.plot([xa,xc],[ya,sc],label='incidende') plt.plot([xc,xb],[sc,yb],label='reflejado') plt.plot([xa,xb],[sc,sc],label='suelo') # etiquetas anotadas plt.annotate(' reflejo',[xc,sc]) # etiquetas plt.legend() plt.xlabel('x') plt.ylabel('y') plt.title('reflexión de rayos en plano') plt.grid() plt.show()
Tarea:
a) Añadir la trayectoria directa del rayo entre el transmisor y receptor
b) Considerar que el plano puede estar inclinado respecto al eje de las x,por lo que para igualar las pendientes del rayo incidente y reflejado se referencian con la pendiente del plano.
m_s = \frac{\Delta suelo } {\Delta x_{intervalo}} = \frac{s_b-s_a}{x_b-x_a} -(m_z-m_s) = m_r-m_s -m_z = m_r - 2 m_s4.1 Movimiento circular – Una partícula, animación con matplotlib-Python
Simular el movimiento circular de una partícula en el plano x,y considerando la variable tiempo consiste en definir las ecuaciones a usar para cada eje.
donde T es el periodo de la función.
Para la gráfica se crean todas las muestras de los puntos en los tiempos ti que al graficarse mostraría un punto en cada posición ti. La animación consiste en usar el concepto de fotograma, una «foto» por unidad de tiempo como en el cine, es decir solo dibujar un punto a la vez, por cada foto ‘i’.
Los fotogramas dentro de un periodo se definen como fotos=20, y el retardo dt en milisegundos dentro del periodo es t/fotos*1000.
La animación requiere usar los procedimientos redibuja(i) y borrapizarra() para cada fotograma ‘i’. Los procedimientos usados o coordinados con la instrucción animation.FuncAnimation()
En caso de requerir un archivo gif animado se proporciona un nombre de archivo. Para crear el archivo se requiere de un complemento ‘imagemagick‘ a ser instalado.
# FCNM-ESPOL-2015. Fisica con Python # Una particula en recorrido circular # propuesta: edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation # INGRESO T = 4 # periodo en segundos x_t = lambda t: np.cos(2*np.pi*t/T) y_t = lambda t: np.sin(2*np.pi*t/T) # intervalos ejes x,y x_a = -1.2 ; x_b =-x_a # simétricos a 0 y_a = -1.2 ; y_b =-y_a fotos = 20 # muestras en un periodo retardo = int(T/fotos*1000) # milisegundos entre fotogramas narchivo = 'movimientocircular01' # archivo.gif # PROCEDIMIENTO # Inicializa valores de muestras i = np.arange(0, fotos) # cuenta tramas ti = np.linspace(0,T,fotos+1) xi = x_t(ti) yi = y_t(ti) # SALIDA - Gráfica animada figura, graf_xy = plt.subplots() graf_xy.axis([x_a, x_b, y_a, y_b]) graf_xy.set_aspect('equal') graf_xy.grid() graf_xy.set_xlabel('x(t)') graf_xy.set_ylabel('y(t)') graf_xy.set_title('movimiento circular') punto, = graf_xy.plot(xi[0], yi[0],'ro') # cuadros de texto en gráfico txt_x = (x_b+x_a)/2 txt_y = y_b*(1-0.09) txt_ti = graf_xy.text(txt_x,txt_y,'t='+str(ti[0]), horizontalalignment='center') # Animación Nueva graf_xy (n frame) def redibuja(i): # actualiza el punto punto.set_xdata(xi[i]) punto.set_ydata(yi[i]) # actualiza texto t_trama = np.around(ti[i],2) txt_ti.set_text('t= '+str(t_trama)) return (punto,txt_ti) def borrapizarra(): # limpiar gráfica punto.set_ydata(np.ma.array(xi, mask=True)) txt_ti.set_text('') return (punto,txt_ti) # Animación coordina ani = animation.FuncAnimation(figura, redibuja, i , init_func=borrapizarra, interval = retardo, blit=True) # Graba Archivo GIFAnimado y video, requiere 'imagemagick' #ani.save(narchivo+'_GIFanimado.gif',writer='imagemagick') plt.show()
Otros ejercicios donde las animaciones son un complemento para mostrar resultados en otros cursos:
Gráfica animada para interpretar el Integral de convolución – Señales y Sistemas
Método de la Bisección – Concepto – Métodos Numéricos
Ecuaciones Diferenciales Parciales Parabólicas – Métodos Numéricos
4.2 Movimiento circular velocidad(t)- gráficas y animación con matplotlib-Python
Se añaden los componentes de velocidad por cada eje al algoritmo de movimiento circular de una partícula para obtener el resultado siguiente
donde T es el periodo de la función.
Los vectores de velocidad son líneas que parten desde la posición de la partícula y se extienden en magnitud de cada componente de la velocidad
vx, = graf_xy.plot([xi[0],xi[0]+vxi[0]],
[yi[0],yi[0]],'*-.')
vy, = graf_xy.plot([xi[0],xi[0]],
[yi[0],yi[0]+vyi[0]],'*-.')
en cada procedimiento redibuja(i) y borrapizarra() se incorpora el nuevo componente para actualizar las coordenadas y en la salida return().
Al incorporar los vectores de velocidad, se debe extender los intervalos de cada eje, con un exceso de 0.2 como espacio para mostrar el cuadro de texto para la variable tiempo.
Instrucciones en Python
# FCNM-ESPOL-2015. Fisica con Python # velocidad de una particula en recorrido circular # propuesta: edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation # INGRESO T = 4 # periodo en segundos x_t = lambda t: np.cos(2*np.pi*t/T) y_t = lambda t: np.sin(2*np.pi*t/T) # velocidades v_x = lambda t: -(2*np.pi/T)*np.sin(2*np.pi*t/T) v_y = lambda t: (2*np.pi/T)*np.cos(2*np.pi*t/T) # intervalos ejes x,y x_a = -1.8-.2 ; x_b =-x_a # simétricos a 0 y_a = -1.8-.2 ; y_b =-y_a fotos = 40 # muestras en un periodo retardo = int(T/fotos*1000) # milisegundos entre fotogramas narchivo = 'movimientocircular02' # archivo.gif # PROCEDIMIENTO # Inicializa valores de muestras i = np.arange(0, fotos) # cuenta tramas ti = np.linspace(0,T,fotos+1) xi = x_t(ti) yi = y_t(ti) vxi = v_x(ti) vyi = v_y(ti) # SALIDA - Gráfica animada figura, graf_xy = plt.subplots() graf_xy.axis([x_a, x_b, y_a, y_b]) graf_xy.set_aspect('equal') graf_xy.grid() graf_xy.set_xlabel('x(t)') graf_xy.set_ylabel('y(t)') graf_xy.set_title('movimiento circular') punto, = graf_xy.plot(xi[0], yi[0],'ro') # dibuja velocidad velocidad, = graf_xy.plot([xi[0],xi[0]+vxi[0]], [yi[0],yi[0]+vyi[0]],'*-') vx, = graf_xy.plot([xi[0],xi[0]+vxi[0]], [yi[0],yi[0]],'*-.') vy, = graf_xy.plot([xi[0],xi[0]], [yi[0],yi[0]+vyi[0]],'*-.') # Dibuja trayectoria circular trayecto = graf_xy.plot(xi,yi,linestyle='dotted') # cuadros de texto en gráfico txt_x = (x_b+x_a)/2 txt_y = y_b*(1-0.09) txt_ti = graf_xy.text(txt_x,txt_y,'t='+str(ti[0]), horizontalalignment='left') # Animación Nueva graf_xy (n frame) def redibuja(i): # actualiza el punto punto.set_xdata(xi[i]) punto.set_ydata(yi[i]) # actualiza velocidad velocidad.set_xdata([xi[i],xi[i]+vxi[i]]) velocidad.set_ydata([yi[i],yi[i]+vyi[i]]) vx.set_xdata([xi[i],xi[i]+vxi[i]]) vx.set_ydata([yi[i],yi[i]]) vy.set_xdata([xi[i],xi[i]]) vy.set_ydata([yi[i],yi[i]+vyi[i]]) # actualiza texto t_trama = np.around(ti[i],2) txt_ti.set_text('t= '+str(t_trama)) return (punto,txt_ti,velocidad,vx,vy) def borrapizarra(): # limpiar gráfica punto.set_ydata(np.ma.array(xi, mask=True)) velocidad.set_ydata(np.ma.array(xi, mask=True)) vx.set_ydata(np.ma.array(xi, mask=True)) vy.set_ydata(np.ma.array(xi, mask=True)) txt_ti.set_text('') return (punto,txt_ti,velocidad,vx,vy) # Animación coordina ani = animation.FuncAnimation(figura, redibuja, i , init_func=borrapizarra, interval = retardo, blit=True) # Graba Archivo GIFAnimado y video, requiere 'imagemagick' ani.save(narchivo+'_GIFanimado.gif',writer='imagemagick') plt.show()
3.1 Equilibrio Fuerzas – Grafica Vectores con Python
Fuerzas en equilibrio y Vectores , vectores, gráficas
Suma de vectores dadas las magnitudes y ángulos en grados sexagesimales, algoritmo usando Python.
Cuántos vectores:2 Componentes de los vectores: magnitud[0]:1 angulo[0] (a°):50 magnitud[1]:2 angulo[1] (a°):160 magnitud: 1.905759540628703 ángulo: -49.543247280259386 grados
Para el ejercicio los vectores se expresan en magnitud y ángulo, los datos se ingresan en arreglos separados pero relacionados por el índice.
Para realizar las gráficas se cambian los vectores a coordenadas cartesianas, dado que la instrucción de gráfica de flechas requiere los puntos de partida y los puntos de llegada.
Instrucciones en Python
# FCNM-ESPOL-2015 # Graficar suma de vectores como trapecio # Propuesta: Edison Del Rosario/ # edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt # INGRESO de datos n = int(input('Cuántos vectores:')) print('Componentes de los vectores:') A = np.zeros(n, dtype=float) alfa = np.zeros(n, dtype=float) i = 0 while (i<n): A[i] = float(input('magnitud['+str(i)+']:')) alfa[i] = float(input('angulo['+str(i)+'] (a°):')) i = i+1 # PROCEDIMIENTO # cambia coordenadas a cartesianas Ax = np.zeros(n, dtype=float) Ay = np.zeros(n, dtype=float) i = 0 while (i<n): Ax[i] = A[i]*np.cos(alfa[i]*2*np.pi/360) Ay[i] = A[i]*np.sin(alfa[i]*2*np.pi/360) i = i+1 # Calcular Resultante i = 0 Sx = 0 Sy = 0 while (i<n): Sx = Sx + Ax[i] Sy = Sy + Ay[i] i = i+1 magnitud = np.linalg.norm([Sx,Sy]) grados = np.arctan(Sy/Sx)*(180/np.pi) # Ubicar la posicion inicial de los vectores px = np.zeros(n, dtype=float) py = np.zeros(n, dtype=float) # SALIDA de resultados print('magnitud: '+str(magnitud)) print('ángulo: '+str(grados)+' grados') # límites de los ejes xmin = np.min([np.min(Ax),Sx,np.min(px)]) xmax = np.max([np.max(Ax),Sx,np.max(px)]) ymin = np.min([np.min(Ay),Sy,np.min(py)]) ymax = np.max([np.max(Ay),Sy,np.max(py)]) limite=np.array([xmin,xmax, ymin,ymax]) plt.axis(limite) # grafica de vectores plt.quiver(px,py,Ax,Ay, color='blue', angles='xy', scale_units='xy', scale=1) # grafica de vector suma plt.quiver(0,0,Sx,Sy, color='green', angles='xy', scale_units='xy', scale=1, label = 'resultante') plt.title('Suma de '+str(n)+' vectores') plt.legend() plt.show()
2.6 Cinemática – Gráficas y subgráficas con Python
Referencia: Sears-Zemansky Vol1 Cap2.3 Vol1 Ed.12 p79. Ejemplo 3.16. Diapositivas. Movimiento de proyectiles
1. TALLER – Movimiento de proyectiles
La bola roja se deja caer desde el reposo y la amarilla se proyecta horizontalmente al mismo tiempo; las imágenes sucesivas en esta fotografía estroboscópica están separadas por intervalos de tiempo iguales.
En un instante dado, ambas bolas tienen la misma posición “y”, velocidad “y” y aceleración “y”, a pesar de tener diferente posición “x” y velocidad “x”.
Realizar la simulación usando Python, siguiendo las instrucciones dadas:
- Determinar el intervalo de tiempo a usar
- Determinar los valores iniciales de posición y velocidad para cada componente.
- Inicializar y calcular la tabla de datos.
- Suponer intervalos de medición unitarios
- Calcular los valores de x(i), y(i) con las formulas conocidas.
Presentar la gráfica de resultados
Resultado esperado:
2. Taller – Graficar las componentes
Se puede realizar una presentación tipo vista vertical, y vista horizontal, combinada usando
grafica, cuadro=plt.subplots(2,2)
Se dibujan los gráficos en cada cuadro, seleccionado por posición de fila y columna
cuadro[0,0].scatter(x2,y2,c='r',marker='o') cuadro[0,1].scatter(x,y,c='y',marker='o') cuadro[1,1].scatter(x3,y3,c='b',marker='o') plt.show()
Puede añadir títulos y tramas a cada recuadro
3. Caida Libre
Una introducción a la física con Python, simular la caída de un objeto por varios segundos, graficando su posición en el espacio. La gráfica a mostrar es semejante a la del libro de Sears-Zemansky,
Lo más importante, es conocer del ejercicio en Física y seguir los pasos de forma ordenada. Es Física, simulando con programación..!
Instrucciones Python
# Primer programa de caída libre # Una pelota se deja caer desde x0=1 m # Desde una altura de 50 m # Se observa en un tiempo [0,tn) # edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt # INGRESO tn = int(input('¿Cuantos segundos?:')) # condiciones iniciales t0 = 0 x0 = 1 y0 = 50 # PROCEDIMIENTO # muestras del experimento x=np.zeros(tn,dtype=float) y=np.zeros(tn,dtype=float) t=np.zeros(tn,dtype=float) # aplica condiciones iniciales t[0]= t0 x[0]= x0 y[0]= y0 # calcula los puntos siguientes i=1 while (i<tn): t[i]=t[i-1]+1 x[i]=x[0] y[i]=y[0]+0*t[i]+0.5*(-9.8)*(t[i]**2) i=i+1 # SALIDA - Gráfica plt.scatter(x,y) plt.ylabel('altura') plt.xlabel('eje x') plt.show()
Actividad Independiente:
a) Usando el archivo «caidalibreUnaPelota.py«, modificarlo para añadir una seguna pelota que inicia en la misma posición, pero con velocidad inicial en el eje de las x, v0x, la cual puede ser, positiva o negativa.
b) Generar las graficas de t vs y para ambos casos y comparar resultados.
2.5 Cinemática – Gráficas tiempo vs distancia con Python
Referencia: Sears-Zemansky Cap2.2 Vol1 Ed.12 p39
Diapositivas: Graficando tiempo vs distancia, velocidad y aceleración.
Situación propuesta: Observar en una gráfica los datos del ejercicio anterior.
Tomar lecturas de distancias y tiempos recorridos, para obtener velocidades por tramo en Kmh
Usaremos los resultados del ejercicio: velocidadtramos.py
Ejecutar el archivo con los datos del problema mostrado para obtener en memoria los resultados siguientes mostrados.
>>> d array([ 0., 100., 200., 300.]) >>> t array([ 0, 5, 9, 15]) >>> v array([ 0. , 20. , 25. , 16.66666667]) >>> vkmh array([ 0., 72., 90., 60.]) >>>
1. Gráfica desde linea de instrucciones
Se puede crear la gráfica paso a paso desde el Shell de
Python
Se requiere importar la librería para gráficas con el álias “plt” que es estandarizado.
>>> import matplotlib.pyplot as plt
Se crea la línea a graficar
>>> plt.plot(t,d)
Mostrar el gráfico construido
>> plt.show()
2. Añadir títulos de gráfico
>>> import matplotlib.pyplot as plt
Usar la forma interactiva para generar el gráfico, No se usa en el script
>>> plt.ion()
>>> plt.plot(t,d)
[<matplotlib.lines.Line2D object at 0x05A605F0>]
>>> plt.title('Distancia recorrida vs tiempo acumulado')
<matplotlib.text.Text object at 0x05A50630>
>>> plt.xlabel('tiempo segundos')
<matplotlib.text.Text object at 0x05A0A910>
>>> plt.ylabel('distancia en metros')
<matplotlib.text.Text object at 0x05A3C430>
Desconetar la interactiva con plt.ioff() y en el script:
>>> plt.show()
3. Colores y marcas de punto
Nos permiten realizar las gráficas de datos disponibles en un arreglo.
Se utiliza: plt.plot ( x, y, propiedades);
Las propiedades como el color y el punto se especifican entre apóstrofes:
| Letra | Color | Símbolo | forma | |
| b | Blue (azul) | . | Punto | |
| g | Green(verde) | o | círculo | |
| r | Red (rojo) | x | Marca de X | |
| y | Yellow (amarillo) | + | Marca de + | |
| k | Black (negro) | s | cuadro | |
| w | White(blanco | v | Triángulo | |
| m | magenta | o | pentagrama |
las instrucciones a usar son:
>>> plt.plot(t,v,'ro-')
[]
>>> plt.title('velocidad observada vs tiempo acumulado')
>>> plt.xlabel('tiempo en segundos')
>>> plt.ylabel('velocidad en m/s')
>>> plt.show()
con lo que se obtiene
Taller – Aceleración media
Referencia: Física Universitaria Sears –Zemanski. Vol 1. Edición 12. Ejercicio 2.12
(2.12). Un piloto de pruebas de Automotores Galaxia, S.A., está probando un nuevo modelo de automóvil con un velocímetro calibrado para indicar m/s en lugar de mi/h. Se obtuvo la siguiente serie de lecturas durante una prueba efectuada en una carretera recta y larga:
| tiempo(s) | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| Rapidez(m/s) | 0 | 0 | 2 | 6 | 10 | 16 | 19 | 22 | 22 |
a) Calcule la aceleración media en cada intervalo de 2 s.
¿La aceleración es constante? ¿Es constante durante alguna parte de la prueba?
b) Elabore una gráfica vx – t con los datos, usando escalas de 1 cm = 1 s horizontalmente, y 1 cm = 2 m/s verticalmente.
Dibuje una curva suave que pase por los puntos graficados.
Mida la pendiente de la curva para obtener la aceleración instantánea en: t =9 s, 13 s y 15 s.
Desarrollar el literal a) en Python
tiempo = [0.0, 2, 4, 6, 8, 10, 12, 14, 16]rapidez = [0, 0, 2, 6, 10, 16, 19, 22, 22]
4. Subgráficos (subplots)
Permiten realizar grupos de gráficos en un esquema tipo matricial.
gráfica, cuadro=plt.subplots(2) 
El índice del primer cuadro es el cer0
cuadro[0].plot(x,y)
El siguiente cuadro es el uno
cuadro[1].step(tiempo,acelera,’r’)
Se pueden añadir o cambiar las propiedades de un cuadro:
cuadro[0].set_title(‘tiempo vs rapidez’)
Las instrucciones en Python desde la toma de datos son
# FCNM-ESPOL. Física con python # calcular aceleracion media por intervalo import numpy as np import matplotlib.pyplot as plt # INGRESO puntos = int(input('¿puntos observados?:')) tiempo = np.zeros(puntos,dtype=int) rapidez = np.zeros(puntos,dtype=float) i = 0 while (i<puntos): tiempo[i] = int(input('tiempo transcurrido (s):')) rapidez[i] = float(input('distancia recorrida (m/s):')) i = i + 1 # PROCEDIMIENTO acelera = np.zeros(puntos,dtype=float) i = 0 acelera[0] = 0 i = 1 while (i<puntos): acelera[i] = rapidez[i]-rapidez[i-1] i = i + 1
En el bloque de salida se puede añadir:
#grafica con dos cuadros grafica,cuadro = plt.subplots(2) cuadro[0].plot(tiempo,rapidez) cuadro[0].set_title('tiempo vs rapidez') cuadro[0].set_ylabel('rapidez (m/s)') cuadro[1].step(tiempo,acelera,'r') cuadro[1].set_title('tiempo vs aceleracion media') cuadro[1].set_xlabel('tiempo (s)') cuadro[1].set_ylabel('aceleracion (m/s2)') plt.show()
2.4 Cinemática – Contadores, Acumuladores y arreglos
Referencia: Sears-Zemansky Cap2.2 Vol1 Ed.12 p39
Diapositivas: identificando cada punto observado.
Situación Propuesta
Identificar cada lectura de datos para el ejercicio de velocidad por tramos requiere un índice o número que sea único para cada lectura.
Se usa el concepto de contadores y acumuladores para llevar el control de los índices:
Contadores y Acumuladores en programación
Los arreglos permiten almacenar listas de datos, tal como las usadas en el ejemplo anterior:
>>d(1) Ans = 100 >> t(3) Ans=15
se observa que todas las variables tipo arreglo tienen:
Taller: Velocidad media
En el ejercicio mostrado, calcular la velocidad media como el promedio de los valores de velocidades.
2.3 Cinemática – lazos/bucles y arreglos 1D, velocidad por tramos con Python
Referencia: Sears-Zemansky Cap2.2 Vol1 Ed.12 p39
Diapositivas: Con varios puntos observados.
Situación propuesta
Tomar lecturas de distancias y tiempos recorridos, para obtener velocidades por tramo en Kmh
Lazos para Repetir
Usados cuando hay que repetir una operación o bloque de procedimiento. Se expresa como:
Mientras (condición): repita while (condición): …
Lazos/Bucles – Estructuras para Repetir o iterar
Vectores – Arreglos de una dimensión
Usados cuando hay que almacenar una lista de datos, similar a la del problema propuesto. 
Se requiere importar la librería numpy para facilitar el manejo de los datos. np es el alias de la librería
import numpy as np
Se inicializa el arreglo, llenándolo con ceros
d=np.zeros(puntos,dtype=float) t=np.zeros(puntos,dtype=int) i=0
Los arreglos inician en la fila 0, conocida como punto inicial.
Es necesario indicar los datos son enteros(int) o reales (float).
Vectores – Arreglos de una dimensión
resultado del algoritmo:
>>> ¿puntos observados?:4 distancia recorrida (m):0 tiempo transcurrido (s):0 distancia recorrida (m):100 tiempo transcurrido (s):5 distancia recorrida (m):200 tiempo transcurrido (s):9 distancia recorrida (m):300 tiempo transcurrido (s):15 Velocidades en Kmh: 0.0 72.0 90.0 60.0
Algoritmo: Velocidad por tramos recorridos
# FCNM-ESPOL. Física con python # varios tramos de recorrido import numpy as np puntos=int(input('¿puntos observados?:')) d=np.zeros(puntos,dtype=float) t=np.zeros(puntos,dtype=int) i=0 while (i<puntos): d[i]=float(input('distancia recorrida (m):')) t[i]=int(input('tiempo transcurrido (s):')) i=i+1 #Procedimiento v=np.zeros(puntos,dtype=float) vkmh=np.zeros(puntos,dtype=float) v[0]=0 vkmh[0]=0 i=1 while (i<puntos): v[i]=(d[i]-d[i-1])/(t[i]-t[i-1]) vkmh[i]=(v[i]/1000)*60*60 i=i+1 #Salida print('Velocidades en Kmh:') i=0 while (i<puntos): print(vkmh[i]) i=i+1
Ejercicio para Taller
Velocidades por tramos, Implementar el algoritmo en python.
| Lectura | d | t | V | V |
| metros | seg | m/s | Kmh | |
| 0 | 0 | 0 | ||
| 1 | 100 | 5 | ||
| 2 | 200 | 9 | ||
| 3 | 300 | 15 | ||
| 4 | 400 | 19 | ||
| 5 | 500 | 25 | ||
| 6 | 600 | 33 | ||
| 7 | 700 | 38 | ||
| 8 | 700 | 45 | ||
| 9 | 800 | 55 | ||
| 10 | 800 | 15 |