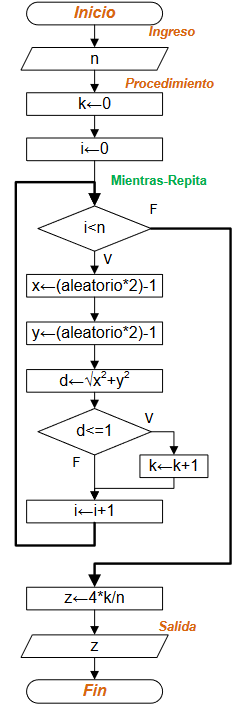
Ejercicio: 1Eva_IIT2004_T3 Estimar π por Montecarlo
Ingresar n como la cantidad de puntos en el plano a ubicar de forma aleatoria dentro del rango del cuadrado que inscribe al círculo.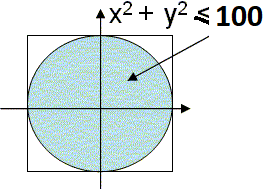 
Usar una variable “k” como el contador para los puntos que caen dentro del círculo.
Al generar cada punto se puede calcular la distancia al centro mediante Pitágoras.
d= \sqrt{x^2 +y^2}Se repite el proceso para n puntos y al final se calcula el valor estimado de pi acorde a la relación presentada.
Nota: no se usa como variable la palabra “pi” debido a que es nombre de variable reservada.
Instrucciones en Python
# 1Eva_IIT2004_T3 Estimar Pi por Montecarlo # Propuesta de solución. edelros@espol.edu.ec # se usa todo el círculo import random as rnd import numpy as np # INGRESO n = int(input('¿Cuántos puntos?: ')) radio = 1 # PROCEDIMIENTO punto = np.zeros(shape=(n,2),dtype=float) k = 0 i = 0 while i<n: x = rnd.random()*(2*radio)-1 y = rnd.random()*(2*radio)-1 d = np.sqrt(x**2+y**2) if d<=radio: k = k + 1 punto[i] = [x,y] i = i + 1 estimadopi = 4*k/n # SALIDA print(k,n) print('estimador pi: ', estimadopi) print(punto)
la estimación de π con números aleatorios que se ubican dentro del círculo de radio 1 es:
¿Cuántos puntos?: 1000 781 1000 estimador pi: 3.124 [[ 0.15581724 0.43992571] [-0.11114653 -0.86426905] [ 0.51257751 -0.1969925 ] ... [ 0.26965478 -0.01555604] [-0.89575602 0.56077385] [ 0.33467618 -0.59497405]] >>>
Diagrama de Flujo
