condicionales – Página 3 – Fundamentos de Programación

2014-03-122022-07-27

1Eva_IT2007_T1 Tiro al blanco con dardos

1ra Evaluación I Término 2007 – 2008. Julio 03, 2007 /ICM00794

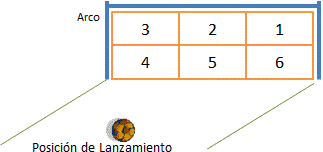
Tema 1 (30 puntos) “Tiro al blanco” es un juego que consiste en 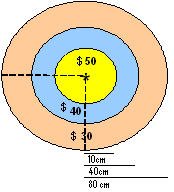lanzar dardos a un objetivo circular.

El premio que gana el jugador, depende de la ubicación en la cual cae el dardo y su valor se reparte en dólares ($30, $40 o $50), tal como se muestra en la figura:

Existen 3 círculos concéntricos (que tienen el mismo centro) y las longitudes de los radios del primero, segundo y tercer círculos son 10cm, 40cm y 80cm, respectivamente.

Suponga que los 3 círculos están inscritos en un cuadrado de longitud de lado 160cm.

Escriba un algoritmo que permita simular n lanzamientos aleatorios de dardos, asignando de forma aleatoria pares ordenados (x, y) en el cuadrado descrito.

En cada lanzamiento se debe verificar si el dardo se ubica al interior de alguno de los círculos descritos y asignar el respectivo premio.

Al final, muestre el premio total en dólares que obtuvo el jugador.

Nota: La distancia entre dos puntos en el plano P1(x₁, y₁) y P2(x₂, y₂), viene dada por la siguiente expresión matemática:

d(P_1,P_2) = \sqrt{(x_2-x_1)^2 +(y_2-y_1)^2 }

2014-03-112023-02-04

1Eva_IIT2011_T1 Número+2 tiene raíz cubica exacta

1ra Evaluación II Término 2011-2012. Noviembre 29, 2011 /ICM00794

Tema 1. (20 puntos) El número 5 tiene la propiedad que al sumar el número 2 a su cuadrado, se obtiene un número que tiene raíz cúbica exacta: 5² + 2 = 27 .

Realice un algoritmo que busque entre los números enteros menores al 1000, si existe algún otro número que al sumar 2 a su cuadrado el resultado tiene raíz cúbica exacta.

Rúbrica: Inicialización de variables (5 puntos), operaciones y búsqueda (10 puntos), resultados (5 puntos).

2014-03-112023-02-04

1Eva_IT2011_T1 Ahorros de Juan vs Pedro

1ra Evaluación I Término 2011-2012. Julio 5, 2011 /ICM00794

Tema 1. (20 puntos). Una persona que deposita C dólares en una cuenta de ahorros, el banco le paga una tasa de interés anual r, luego de n años tendrá un valor acumulado de A dólares.

La siguiente expresión matemática relaciona estos valores:

A=C(1+r)^n

Juan y Pedro abren cuentas de ahorros en diferentes bancos.

En el banco X, Juan deposita en una cuenta de ahorros C=200 que paga un interés anual de r=0.08.
En el banco Y, Pedro deposita en otra cuenta de ahorros C=300 que paga un interés anual de r=0.05.

Escriba un algoritmo que solicite los datos para las cuentas de Juan y Pedro, determine el año n cuando la cantidad acumulada A de Juan superará a la cantidad acumulada A de Pedro.

Nota: Para el algoritmo no se considerarán depósitos o retiros entre los años. Suponga que Juan deposita menos que Pedro y que el interés del Banco X es mayor que Y.

Rúbrica: Ingreso de datos (5 puntos), determinación de saldos individuales por año (5 puntos), respuesta solicitada (10 puntos)

2014-03-102023-02-04

1Eva_IIT2010_T2 Venta de pasajes tren turístico

1ra Evaluación II Término 2010-2011. Diciembre 7, 2010 /ICM00794

Tema 2 (30 puntos) En la estación de un tren turístico se instalará una máquina automática para la venta de pasajes que acepta billetes en dólares, euros y pesos.

El comprador indicará el número de pasajes, tipo de moneda y la cantidad de dinero con lo cual la maquina realiza la conversión a pesos, ejecuta el cobro y de ser necesario entrega el cambio en pesos.

Suponga que el tren tiene capacidad para 150 pasajeros, que el tipo de cambio es 2.5 pesos/dólar, 3.25 pesos/euro y que el precio del pasaje es de 7 pesos.

Escriba un algoritmo que simule la máquina de venta de pasajes, para n turnos de compra o hasta completar la capacidad tren, considerando que un comprador puede pedir más de un boleto.

La maquina vende los pasajes cuando el comprador entrega la cantidad suficiente de dinero y aún hay asientos disponibles.

Al final de las ventas muestre la cantidad de boletos vendidos, total de pesos cobrados y devuelto como cambio.

Ejemplo:
 ¿Cuantos turnos?: 5 
 Turno 1 
  ¿cuántos pasajes?: 3
  Monedas: 1.Dolar 2.Euro 3.Peso
  ¿Tipo Moneda?: 1
  ¿Cantidad de Dinero?: 10
  su cambio: 4
 Turno 2 
  ¿Cuántos pasajes?:
 …

Rúbrica: Ingreso de datos (5 puntos), cobro y cambio (10 puntos), validar ventas y asientos (10 puntos). Algoritmo integrado (5 puntos).

2014-03-072023-02-04

1Eva_IIT2007_T1 Hormiga busca arroz

1ra Evaluación II Término 2007 – 2008. Diciembre 04, 2007 /ICM00794

Tema 1. (30 puntos)

En un plano cartesiano se encuentran una hormiga y un grano de arroz.

En cada instante de tiempo, la hormiga de manera aleatoria intuye la dirección donde ir (arriba, abajo, derecha, izquierda), y cuantas unidades desplazarse (entre 1 a 3) en la anterior dirección.

Implemente un algoritmo que simule 100 instantes de tiempo con desplazamientos de la hormiga que inicialmente se encuentra en las coordenadas (-2,2) y un grano de arroz en las coordenadas (10,8).

Al final indique las respuestas a las siguientes preguntas:

a) ¿La hormiga llegó al grano de arroz?

b) Si la respuesta a la pregunta anterior es “Si”, entonces mostrar: cuántos pasos fueron necesarios.

c) ¿La distancia más lejana en la que estuvo la hormiga del grano de arroz?

Nota: La distancia entre dos puntos en el plano P1(x1, y1) y P2(x2, y2), viene dada por la siguiente expresión matemática:

d(P_1,P_2) = \sqrt{(x_2-x_1)^2 +(y_2-y_1)^2 }

2014-03-062023-02-04

1Eva_IIT2006_T3 Conejo en tablero

1ra Evaluación II Término 2006 – 2007 /ICM00794

Tema 3. (30 puntos) Suponga que un conejo se encuentra ubicado en el centro de un tablero cercado de 10×10 y con una salida en el lugar que se muestra en la figura.

Si cada vez que el conejo salta 1 casilla, se conoce que lo puede realizar de forma aleatoria hacia arriba, abajo, izquierda o derecha.

Elabore un algoritmo que determine cuántos intentos debe realizar el conejo hasta que sale del tablero.

10									salida
9
8
7
6
5					Inicio
4
3
2
1	…	…	…	…	…	…	…	…	…	…
	1	2	3	4	5	6	7	8	9	10

2014-03-052023-02-04

1Eva_IIT2005_T4 Juego escaleras y serpientes

Parcial II Término 2005 – 2006. Diciembre 06, 2005 /ICM00794

Tema 4. (25 puntos).Para una nueva versión del juego “Escaleras y Serpientes” se desea disponer del algoritmo para simulación en computador.

escaleraserpiente

El juego para dos jugadores consiste en llegar a la meta en primer lugar en un tablero de 64 casillas cuyas especificaciones son las siguientes:

Al inicio los jugadores están en una misma posición y arrancan su trayectoria cuando lanzando una moneda (cara 1 o 2) el jugador que gane empieza.
Cada jugador realiza su recorrido alternadamente de acuerdo a los resultados de los lanzamientos de un dado (6 caras)
Al avanzar, el jugador puede “caer” en una “casilla de castigo”, por lo que retrocederá 3 pasos de la posición en la que se encuentra. Si cae en “casilla de premio”, el usuario avanzará 3 pasos de la posición en la que se encuentra.
Luego de un lanzamiento y determinación de la posición final, el jugador le pasa el turno al otro jugador.
Se repite el juego desde el paso 2 hasta que uno de los jugadores pase la meta.

Al final se deberá mostrar:
– Número de veces jugadas por cada jugador, y
– El jugador que ganó.

Nota: casillas de premio para éste tema son: 4, 9, 29, 34, 46 y de castigo: 8, 19, 38, 50, 60

2014-03-052023-02-04

1Eva_IT2005_T4 Lanza penales

Parcial I Término 2005 – 2006. Julio 05, 2005 /ICM00794

Tema 4. (30 puntos) En el Fútbol el lanzamiento de penales intervienen el jugador que patea y el arquero que tapa el penal.

Este juego consiste en 5 lanzamientos por parte de los jugadores que patean el balón, los cuales pueden decidir lanzar en cualquiera de las seis secciones del arco (1: arriba a la derecha, 2: arriba al centro, 3: arriba a la izquierda, 4 abajo a la izquierda, 5: abajo al centro, 6: abajo a la derecha).

En cada lanzamiento, el arquero decide donde ubicarse para atajar el tiro y no tiene oportunidad de cubrir otra sección, si éste coincide con la ubicación donde disparó el jugador, entonces el lanzamiento fue atajado o fallado, caso contrario se marcó un GOL.

Escriba un algoritmo que simule un juego de 5 lanzamientos de penales, en donde la sección del arco donde cada jugador lanza es decidido por el usuario y la sección cubierta por el arquero es simulado por el computador (aleatoria).

Al final presente la siguiente información:

a) Cantidad de goles conseguidos.

b) Cantidad de penales fallados.

c) La cantidad de goles realizados en la parte derecha, central e izquierda del arco.

d) La ubicación del arco (derecha, centro o izquierda) por donde ingresaron más goles. Suponga que existe una sola.

e) La ubicación del arco (derecha, centro o izquierda) por donde no ingresaron goles. Suponga que existe una sola.

Rúbrica: literal a (5 puntos), literal b (5 puntos), literal c (5 puntos), literal d (5 puntos), literal e (5 puntos), estructuras completas (5 puntos), contadores y acumuladores inicializados y en orden (5 puntos).

2014-03-032023-02-04

1Eva_IIT2003_T2 Sumar términos de progresión geométrica

Parcial II Término 2003 – 2004. Diciembre 09, 2003 /ICM00794

Tema 2. (20 puntos) Escriba un algoritmo que muestre por pantalla el resultado de la suma S de los términos de una progresión geométrica, de primer término a y razón r, con valores de i desde 0 hasta n.

El algoritmo debe solicitar al usuario los valores de a, n y r, y validar que r sea diferente de 1.

S = \sum_{i=0}^{n} a + ar + ar^2 + ar^3 + ... + ar^n

Referencia: UCC+1,Predicen la evolución de la progresión geométrica del COVID-19