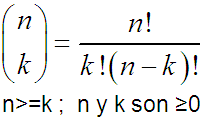2da Evaluación II Término 2014-2015, Febrero 2015 /FIEC
Tema 1. (25 puntos) Escriba la función recursiva calcularPotenciacion(base,exponente) la cual recibe dos números enteros no negativos como parámetros para calcular y retornar la potenciación de los mismos asumiendo que el primer número es la base y el segundo el exponente.
baseexponente = 24=2.23=2.2.22=2.2.2.2
Nota: No utilizar la función estándar pow (base, exp).
Referencia: 2Eva_IT2005_T2 Calcular potencia recursiva