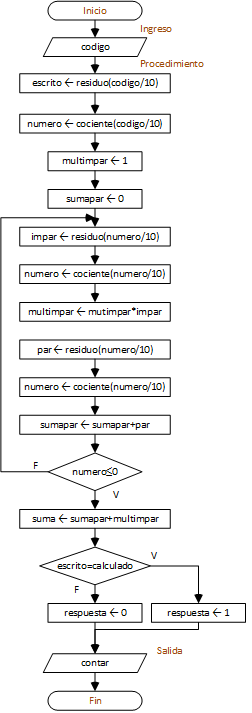
Ejercicio: 1Eva_IIT2005_T4 Juego escaleras y serpientes
Propuesta de solución: python_pdf, matlab_pdf
En un primer bosquejo, no se considera el lanzar la moneda para ver cuál jugador inicia, semejante al ajedrez en que las fichas blancas salen primero sin considerar el nombre del jugador. 
Para determinar las posiciones de las fichas en el tablero, se usarán acumuladores para cada jugador A y B, usando como variables “fichaa” y “fichab”.
# jugador A
dadoa = int(rnd.random()*6)+1
fichaa = fichaa + dadoa
Serán necesarios otras variables como el contador para el turno, cada jugador dispondrá de una variable generada de forma aleatoria que simula un dado de 6 caras.
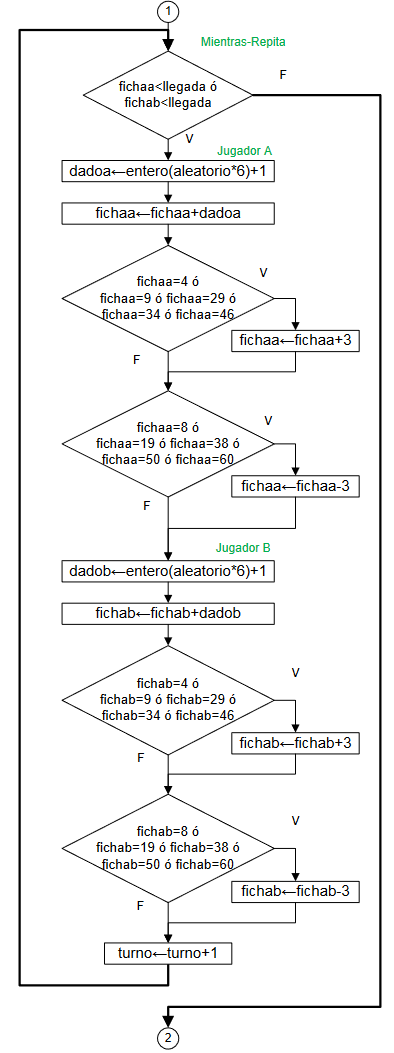
Se lanza el dado para el jugador A, se avanza acumulando conforme a los puntos del dado, se valida el premio o castigo para luego repetir el proceso para el jugador B, repitiendo el proceso hasta que alguna ficha se ubique o pase la casilla de “llegada”.
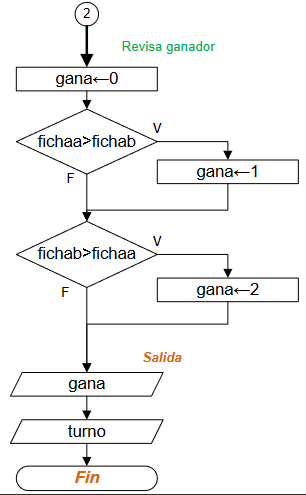
Terminado el proceso anterior, se determina cuál jugador ganó, observe que se supone que gana tiene inicialmente el valor de 0, para tener la opción de registrar un empate.
Al final se muestran los resultados del juego simulado.
Tarea: Resolver con el lanzamiento de la moneda para ver cuál inicia.
Primero se presenta la solución usando lazo “Mientras-Repita” por compatibilidad con Matlab, luego se muestra la versión con el lazo “Repita-Hasta” que se puede escribir en los lenguajes de programación.
Instrucciones en Python. Versión Lazo: Mientras-Repita
# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2005_T4 Juego escaleras y serpientes
# Propuesta de solución: edelros@espol.edu.ec
import random as rnd
# INGRESO
# Sortear quién empieza
# PROCEDIMIENTO
llegada = 64
fichaa = 0
fichab = 0
turno = 0
while (fichaa<llegada or fichab<llegada):
# jugador A
dadoa = int(rnd.random()*6)+1
fichaa = fichaa + dadoa
if (fichaa==4 or fichaa==9 or fichaa==29 or fichaa==34 or fichaa==46):
fichaa = fichaa + 3
if (fichaa==8 or fichaa==19 or fichaa==38 or fichaa==50 or fichaa==60):
fichaa = fichaa - 3
#jugador B
dadob = int(rnd.random()*6)+1
fichab = fichab + dadob
if (fichab==4 or fichab==9 or fichab==29 or fichab==34 or fichab==46):
fichab = fichab + 3
if (fichab==8 or fichab==19 or fichab==38 or fichab==50 or fichab==60):
fichab = fichab - 3
turno = turno + 1
# Revisa ganador
gana = 0
if fichaa > fichab:
gana = 1
if fichab > fichaa:
gana = 2
# SALIDA
print('gana el jugador: ')
print(gana)
print('turnos jugados:')
print(turno)
Ejecución del algoritmo
gana el jugador:
2
turnos jugados:
16
>>>
gana el jugador:
2
turnos jugados:
16
>>>
Instrucciones en Python. Versión lazo: Repita-Hasta
# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2005_T4 Juego escaleras y serpientes
# Propuesta de solución. edelros@espol.edu.ec
import random as rnd
# INGRESO
# Sortear quién empieza
# PROCEDIMIENTO
llegada = 64
fichaa = 0
fichab = 0
turno = 0
while not(fichaa>=llegada or fichab>=llegada):
# jugador A
dadoa = int(rnd.random()*6)+1
fichaa = fichaa+dadoa
if (fichaa==4 or fichaa==9 or fichaa==29 or fichaa==34 or fichaa==46):
fichaa = fichaa+3
if (fichaa==8 or fichaa==19 or fichaa==38 or fichaa==50 or fichaa==60):
fichaa = fichaa - 3
#jugador B
dadob = int(rnd.random()*6)+1
fichab = fichab + dadob
if (fichab==4 or fichab==9 or fichab==29 or fichab==34 or fichab==46):
fichab = fichab + 3
if (fichab==8 or fichab==19 or fichab==38 or fichab==50 or fichab==60):
fichab = fichab - 3
turno = turno+1
gana = 0
if fichaa>fichab:
gana = 1
if fichab>fichaa:
gana = 2
# SALIDA
print('gana el jugador: ')
print(gana)
print('turnos jugados:')
print(turno)
Diagrama de Flujo
ejercicios resueltos Python parc_iit2005_t4 pdf
ejercicios resueltos Matlab parc_iit2005_t4 pdf