Referencia: Gubner 2.2 p.68, León-García E3.7 p.101
Variable aleatoria discreta uniforme
Cuando los resultados de un experimento son igualmente probables o totalmente aleatorios, el modelo se realiza con una variable aleatoria uniforme.
X está distribuida uniformemente si:
P(X=k) = \frac{1}{n} k=1,...,n.la distribución de probabilidad pmf toma solo dos valores:
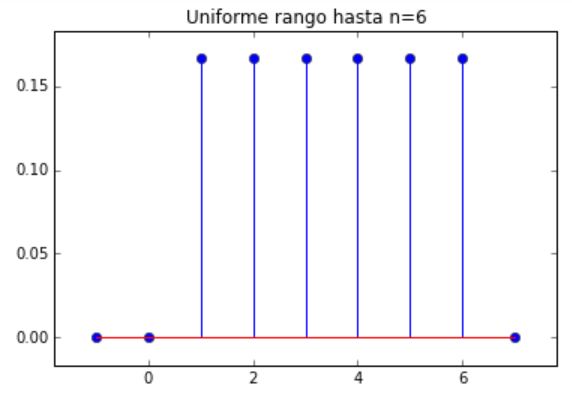
p(k)= \begin{cases} \frac{1}{n}, & \text{k=1,...,n} \\0, & \text{en otro caso} \end{cases}Por ejemplo: el caso de un dado de 6 caras
# Distribución bernoulli con valor p y rango (-1 a 3) import numpy as np import matplotlib.pyplot as plt import scipy.stats as stats # INGRESO n = 6 low = 1 high = low+n # PROCEDIMIENTO k = np.arange(low-2, n+2) p = stats.randint.pmf(k,low,high) # SALIDA print('k: ', k) print('p(k):', p) # grafica plt.title('Uniforme rango hasta n='+str(n)) plt.stem(k,p) plt.margins(0.1) plt.show()
k: [-1 0 1 2 3 4 5 6 7]
p(k): [ 0. 0. 0.16666667
0.16666667 0.16666667 0.16666667
0.16666667 0.16666667 0. ]
Ejemplo
Gubner 2.6. Diez teléfonos inalámbricos en la vecindad,
Leon-García 3.7. Generador de números aleatorios
Diez vecinos tienen cada uno un teléfono inalámbrico de la misma marca y modelo. Suponga que el numero de personas que usa el teléfono inalámbrico al mismo tiempo es totalmente aleatorio. Encuentre la probabilidad que más de la mitad de lso teléfonos se encuentran en uso al mismo tiempo.
Para modelar, el número de teléfonos inalámbricos en uso al mismo tiempo tiene una variable aleatoria discreta uniforme X, que puede tomar valores 0, … , 19. Se incluye el cero al considerar que no hay teléfonos en uso.
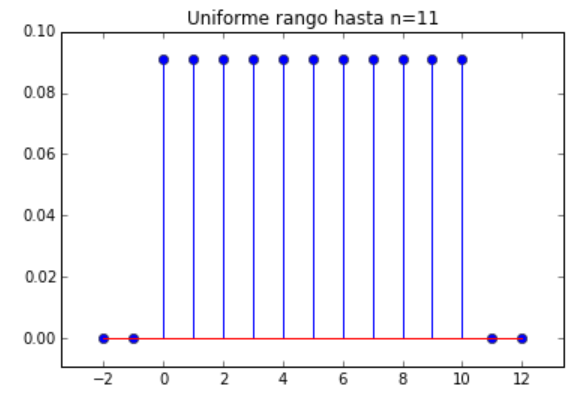
P(X>5)= \sum\limits_{i=6}^{10} p_x(i) = \sum\limits_{i=6}^{10} \frac{1}{11}=\frac{5}{11}# Distribución bernoulli con valor p y rango (-1 a 3) import numpy as np import matplotlib.pyplot as plt import scipy.stats as stats # INGRESO n = 11 low = 0 high = low+n # PROCEDIMIENTO k = np.arange(low-2, high+2) p = stats.randint.pmf(k,low,high) # mas de la mitad en uso desde = n//2 +1 hasta = n pdesde = np.sum(p[desde:hasta]) # SALIDA print('k: ', k) print('p(k):', p) print('mas de la mitad p[X>='+str(desde)+']: ',pdesde) # grafica plt.title('Uniforme rango hasta n='+str(n)) plt.stem(k,p) plt.margins(0.1) plt.show()
k: [-2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12]
p(k): [ 0. 0. 0.09090909
0.09090909 0.09090909 0.09090909
0.09090909 0.09090909 0.09090909
0.09090909 0.09090909 0.09090909
0.09090909 0. 0. ]
mas de la mitad p[X>=6]: 0.454545454545