Referencia: Gubner 2.2 p.68, León-García E3.7 p.101
Variable aleatoria discreta Bernoulli
En un experimento enfocado en situación de "éxito" o "fracaso", por ejemplo un equipo que funciona o no. La variable aleatoria Bernoulli IA es igual a 1 si ocurre un éxito en el grupo A y valor cero en otro caso. La función indicador es por ejemplo:
I_A(\omega) = \begin{cases} 0 && ,\omega\text{ no está en A} \\ 1 && , \omega\text{ está en A} \end{cases}(Revisar modulación Delta-Sigma y la función np.sign(ω))
la distribución de probabilidad pmf toma solo dos valores:
p(k)= \begin{cases} 1-p && , k = 0 \\p &&, k = 1 \end{cases}Note que p0(0) + p1(1) =1
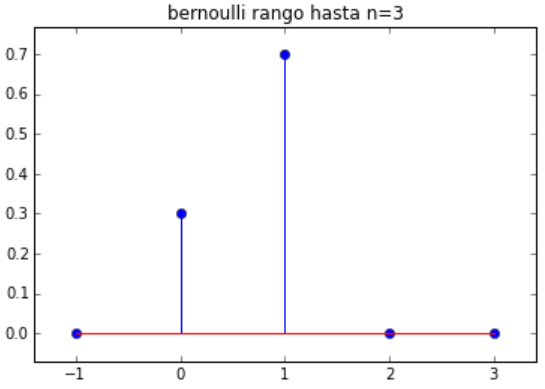
# Distribución bernoulli con valor p import numpy as np import matplotlib.pyplot as plt import scipy.stats as st # ingreso n = 3 p = 0.7 media = 0 # PROCEDIMIENTO k = np.arange(media-1, n+1) px = st.bernoulli.pmf(k,p,media) # SALIDA print('k: ', k) print('p(k):', px) # grafica plt.title('bernoulli rango hasta n='+str(n)) plt.stem(k,px) plt.margins(0.1) plt.show()
k: [-1 0 1 2 3] p(k): [ 0. 0.3 0.7 0. 0. ]
Ejemplo
Las variables aleatorias Bernoulli son buenas para modelar el resultado de un experimento con dos posibles resultados, representados numéricamente como 0 y 1.
- lanzamiento de una moneda
- la prueba de un bloque de un disco de computadora bueno o defectuoso
- si un radar detecta o no una aeronave furtiva
- si un paquete de Internet se descarta debido a la congestión de un router
