1ra Evaluación II Término 2017-2018. Noviembre 28, 2017
Tema 2. (35 puntos) Para comunicar dos ciudades se instalan tres radio-enlaces digitales de larga distancia, cada uno conformado por un transmisor (Tx) y un receptor (Rx). Por ejemplo, las ciudades Guayaquil en la costa y Cuenca en la sierra, se comunican usando tres radio-enlaces que en puntos por tramos en las montañas.
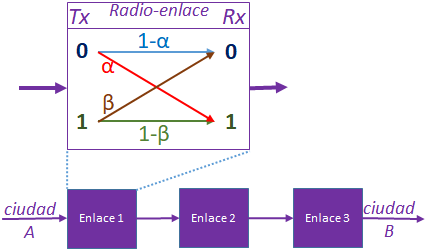
En un radio-enlace el dígito binario 0 enviado por Tx se recibe en Rx con una probabilidad de error α, mientras que el dígito binario 1 presenta probabilidad de error β.
Para un radio-enlace realice un modelo con una Cadena de Markov:
a) Determine el espacio de estados
b) Realice el diagrama de estados, etiquete claramente
c) Escriba la matriz de transición y calcule la probabilidad de estado estable.
Suponga que α=0.01, β=0.02 y determine para todo el enlace entre las ciudades:
d) La matriz de transición entre las ciudades A y B
e) Probabilidad de error para un dígito binario 0 (bit)
f) Probabilidad de error para un bit con valor 1 (bit)
g) El error al transmitir un bit en todo el enlace
h) Observe y comente sus resultados.
Rúbrica: literal a y b (6 puntos), literal c (4 puntos), literal d (10 puntos), literal e y f (3 puntos c/u) literal g (4 puntos), literal h (5 puntos)
Referencia: Gubner(2006) problema 1.56, 3.28, ejemplo 3.13; León-García(2008) 1.5.1; FIEC03236-1ra Evaluación II Término 2011.