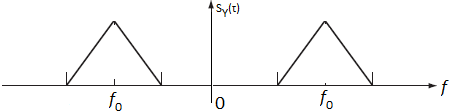Referencia
a) Encuentre la densidad espectral de potencia SY (f) de un proceso aleatorio con función de autocorrelación RX (τ) cos(2π f0 τ), donde RX (τ) es también una función de autocorrelación.
b) Grafique SY (f) si RX (τ) como en el problema 10.1a.
Solución propuesta
R Y ( τ ) = R X ( τ ) cos ( 2 π f 0 τ ) R_Y(\tau) = R_X(\tau) \cos(2\pi f_0 \tau) R Y ( τ ) = R X ( τ ) cos ( 2 π f 0 τ ) S Y ( f ) = F [ R X ( τ ) cos ( 2 π f 0 τ ) ] S_Y(f) = F\Big[ R_X(\tau) \cos(2\pi f_0 \tau) \Big] S Y ( f ) = F [ R X ( τ ) cos ( 2 π f 0 τ ) ] = F [ R X ( τ ) e j 2 π f 0 τ + e − j 2 π f 0 τ 2 ] = F\Big[ R_X(\tau) \frac {e^{j2\pi f_0 \tau} + e^{-j2\pi f_0 \tau}}{2} \Big] = F [ R X ( τ ) 2 e j 2 π f 0 τ + e − j 2 π f 0 τ ] = 1 2 F [ R X ( τ ) e j 2 π f 0 τ ] + 1 2 F [ R X ( τ ) e − j 2 π f 0 τ ] = \frac{1}{2} F\Big[ R_X(\tau) e^{j2\pi f_0 \tau} \Big] + \frac{1}{2} F\Big[ R_X(\tau) e^{-j2\pi f_0 \tau} \Big] = 2 1 F [ R X ( τ ) e j 2 π f 0 τ ] + 2 1 F [ R X ( τ ) e − j 2 π f 0 τ ] = 1 2 S X ( f − f 0 ) + 1 2 S X ( f + f 0 ) = \frac{1}{2} S_X(f-f_0) + \frac{1}{2} S_X(f+f_0) = 2 1 S X ( f − f 0 ) + 2 1 S X ( f + f 0 ) donde SX (f) = F[RX (τ)]