Referencia: León García Ejemplo 9.9 p495, Gubner Ej10.35 p496
Sea X(t) = A cos(2πt), donde A es una variable aleatoria, con un comportamiento semejante a la figura.
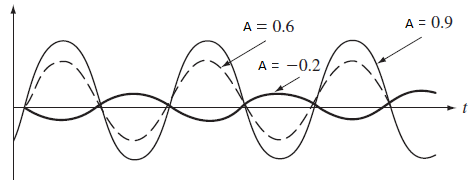
Encontrar el valor esperado , la autocorrelación y autocovarianza de de X(t).
El valor esperado se calcula a continuación, note que la media varia respecto a t y que el valor es cero para valores de t donde cos(2πt) =0.
E[X(t)] = E[A cos(2\pi t)] E[X(t)] = E[A] cos(2\pi t)La autocorrelación es:
R_X(t_1,t_2) = E[A cos(2\pi t_1) A cos(2\pi t_2)] = E[A^{2} cos(2\pi t_1) cos(2\pi t_2)] = E[A^{2}] cos(2\pi t_1) cos(2\pi t_2)usando:
2 cos(x)cos(y) = cos(x-y) + cos(x+y) cos(x)cos(y) = \frac{ cos(x-y) + cos(x + y)}{2}se reemplaza:
= E[A^{2}] \frac{1}{2}[cos(2\pi t_1 - 2\pi t_2) + cos(2\pi t_1 + 2\pi t_2)] R_X(t_1,t_2) = E[A^{2}] \frac{[cos(2\pi (t_1 - t_2)) + cos(2\pi (t_1 + t_2))]}{2}se observa que el valor de autocorrelación depende de las diferencias de tiempo t1 y t2.
La autocovarianza es:
Cov_X(t_1,t_2) = R_X(t_1,t_2) - E[X(t_1)]E[X(t_2)] = E[A^{2}] cos(2\pi t_1) cos(2\pi t_2) - E[A] cos(2\pi t_1)E[A] cos(2\pi t_2) = E[A^{2}] cos(2\pi t_1) cos(2\pi t_2) - E[A]^2 cos(2\pi t_1)cos(2\pi t_2) = (E[A^{2}] - E[A]^2) cos(2\pi t_1)cos(2\pi t_2) = Var[A] cos(2\pi t_1)cos(2\pi t_2)con el mismo procedimiento de cos(x)cos(y):
Cov_X(t_1,t_2) = Var[A] \frac{[cos(2\pi (t_1 - t_2)) + cos(2\pi (t_1 + t_2))]}{2}