ESTG1003 – FCNM – ESPOL
Tema 3 (20 puntos). Dada la función de distribución de probabilidad FX(x), encuentre: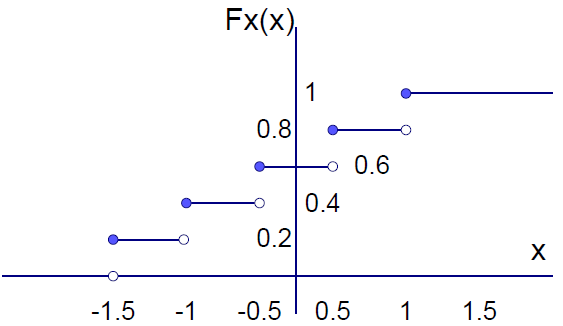 
a) P(X = -0.5)
b) P(|X| ≤ 0.5)
c) Dibuje fX(x|x ≥ -½)
d) Si Y=X+1, dibuje FY(y)
e) Determine Var[Y]
Nota: literal a y b (2 puntos), c y d (6 puntos), e (4 puntos)
Tema 2 (35 puntos). Las variables aleatorias X, Y tienen la siguiente función densidad de probabilidad:
f_{XY}(x,y) = \begin{cases} k && 0 \leq x \leq 1, 0 \leq y \leq 1\\ 2k && 1 \leq x \leq 2, 1 \leq y \leq 2\\0 && \text{otro valor}\end{cases}Determine los siguiente valores:
a) El valor de k para cumplir que sea función densidad de probabilidad
b) P[X ≤ 1,Y ≤ 1]
c) P[X ≤ 1]
d) P[Y ≤ 1|X ≤ 1 ]
e) P[X+Y ≤ 1]
f) P[X ≤ Y2]
Nota: literales a-e (5 puntos), literal f (10 puntos)
Tema 1 (30 puntos). Las variables aleatorias X y Y tienen una distribución conjuntamente uniforme con función densidad conjunta:
fX,Y(x,y) = 2
dentro de la región mostrada en la figura y 0 en otra parte.
Determinar:
a) Encuentre y grafique la pdf marginal para X y Y.
b) Encuentre la correlación y la covarianza de X y Y.
c) ¿X y Y son independientes? Ortogonales? No correlacionadas? Justifique su respuesta.
Rúbrica: 10 puntos cada literal
Tema 4 (25 puntos). Sean dos variables aleatorias X, Y independientes entre si con distribución gausiana con parámetros
E[X] = 2
Var[X] = 2
E[Y] = 0
Var[Y] = 1
Se define la variable Z=X+Y.
Determine la función de densidad de probabilidad fZ(z).
Tema 3 (25 puntos) En una rifa se sacan números aleatorios de dos tómbolas separadas, donde los números posibles de cada tómbola son:
Sea i el número que se obtiene en la tómbola A y k el de la tómbola B.
Si se definen las variables aleatorias X=|i-k| y Y=i+k, determine
a) P[X ≤ 2]
b) Dibuje la fY(Y |x=1)
c) Var(X |y=0)
d) Cov(X, Y)
Tema 2 (25 puntos). La función densidad conjunta de dos variables aleatorias está dada por:
f_{XY}(x,y) = k e^{-x} e^{-2y} 0 \leq y \leq x \leq \inftydeterminar:
a) P[y ≥ x/2]
b) E[Y|x=3]
Tema 1 (25 puntos). Dado FX(x) en la figura y Y=X2, determine:
a) P(x=1) y P(x≤-0.5)
b) Dibuje FY(y)
c) el valor esperado E[Y]
Función densidad de probabilidad conjunta
Tema 4. Para las variables aleatorias X,Y con la función densidad conjunta mostrada, calcule los literales:
f_{XY}(x,y) = \begin{cases} k(x+y) & 0\leq y\leq x\leq3 \\ 0 & \text{otro caso}\end{cases}a) el valor de k , que justifica la función
b) función densidad de probabilidad para Y: fY(y)
c) El valor esperado E[Y|x]
d) Calcule P(0<X+Y<2)
Nota: Dibuje con detalle el área de integración, escriba con claridad los límites de integración, y los rangos de validez donde sea necesario.
Asientos en teatro semicircular
Tema 3. Un teatro romano tiene las gradas en forma de semianillo circular con las dimensiones de la figura.
Cuando se compra una entrada cada asiento es equiprobable (distribución uniforme en las gradas).
a) Determine la función densidad conjunta de probabilidad de la ubicación de un asiento arbitrario.
b) Calcular la función de densidad de probabilidad de la variable aleatoria T que mide la distancia entre el lugar al que corresponde una entrada y el centro del escenario (el origen 0).
c) ¿Cuál es la probabilidad de que un asiento se encuentre ubicado a más de 60 metros a la derecha del eje Y.
Variable aleatoria contínua pdf
Tema 2. Una variable aleatoria contínua X tiene una función densidad de probabilidad (pdf) mostrada en la figura.
a) Determine el valor de a para que sea considere una pdf
b) Determine y realice la gráfica de la función acumulada de probabilidad FX(x).
c) Sea Y una nueva variable aleatoria definida como Y=|X|, determine la pdf de Y y su valor esperado E[Y].
d) Si una nueva variable Z= X2 , encuentre la probabilidad P(Z>Y).