ESTG1003 – FCNM – ESPOL
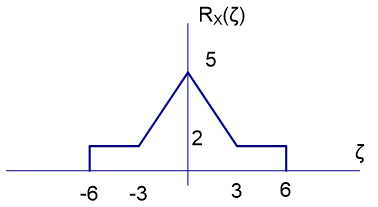
Tema 4 (25 puntos). Sea X(t) un proceso estocastico estacionario en el sentido amplio (WSS) con valor esperado E[X(t)]=a y con una SX(f).
Considere la variable aleatoria Θ con distribución uniforme en (0, 2π) que es independiente de la variable aleatoria definida X(t), y el proceso :
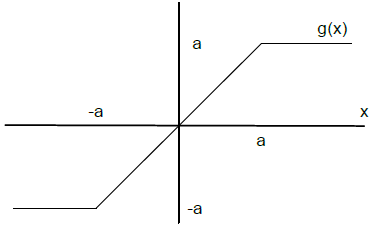
Y(t) = 2 X(t) cos (\omega_0 t + \Theta)a) Determine si el proceso Y(t) es WSS
b) Encuentre SY(f) y SX(f).
Tema 3 (25 puntos). Un proceso estocástico discreto Xn se define como:
Se lanza una moneda balanceada.
Si el resultado es cara:
X_n = (-1)^{n} , \text{para todo n}Si el resultado es sello:
X_n = (-1)^{n+1} , \text{para todo n}a) Dibuje tres realizaciones del proceso estocástico
b) Encuentre la función densidad de probabilidad pmf de Xn
c) Encuentre la función densidad conjunta para Xn y Xn+k
Tema 2 (25 puntos). Dada la siguiente función densidad conjunta:
f_{XY}(x,y)=\begin{cases} k(x^2 + xy) && 0 < x < y < 2 \\ 0 && \text{otrocaso} \end{cases}Calule P[x+y <1]
Tema 1 (25 puntos). Sea X una variable aleatoria con función de densidad de probabilidad uniforme en [-a,a].
Sea Y = g(x) otra variable aleatoria mostrada en la figura:
a) Determine y dibuje la función densidad de Y
b) Determine P[ y < a/2]
Tema 3 (30 puntos). Dada la siguiente función de Autocorrelación Rx(ζ) del proceso estocástico X(t) que es WSS.
a) (15 puntos) Encuentre Var[X(t)]
b) (15 puntos) Sx(w) ( o Sx(f))
Transformadas de Fourier
x(t) \rightarrow X(\omega) g(t) \rightarrow \int_{-\infty}^{\infty} g(t) e^{-j2 \pi ft} dt rect\left( \frac{t}{\tau}\right) \rightarrow \tau sinc\left( \frac{\omega \tau}{2}\right) tri\left( \frac{t}{\tau}\right) \rightarrow \frac{\tau}{2} sinc^2(\frac{\omega \tau}{4})Tema 2 (35 puntos). Sean A y Θ variables aleatorias independientes, A con distribución exponencial de media 1, y Θ con distribución uniforme en el intervalo (0, π/2), es decir las funciones de densidad de A y B son respectivamente:
f_A(a) = e^{-a} , a \in [0,\infty) T_{\Theta}(\theta) = \frac{2}{\pi} , \theta \in [0,\pi /2 ]Sea X(t) un proceso estocástico definido por:
X(t) = e^{-At}cos(\pi t + 4 \Theta) ; t>0Calcular:
a) La media y la autocorrelación del proceso X(t).¿Es el proceso estacionario en sentido amplio?
b) La varianza de X(t) y la covarianza entre X(1) y X(2).
c) La función de densidad de probabilidad para X(0)
cos(a ± b) = cos(a)cos(b) ∓ sen(a) sen(b)
Rúbrica: literal a (10 puntos, literal b (10 puntos), literal c (15 puntos)
Tema 1 (35 puntos). Para las variables aleatorias x,y con la siguiente función densidad conjunta:
f_{XY} (x,y) =\begin{cases} k(x+y) && 0.5 \leq y \leq x , 0.5\leq x\leq 1 \\ 0 && \text{otro caso}\end{cases}Encuentre:
a) (15 pts) Las funciones de densidad marginal de probabilidad, fx(x) y fy(y).
b) (10 Pts) Calcule P[x+y > 3/2].
c) (10 Pts) Calcule P\left[ \frac{Y\leq 0.75}{X+Y \geq 1.5}\right]