Recursos de Estudio – Procesos Estocásticos

6 agosto, 201727 diciembre, 2021

Transformadas de Fourier

Referencia: TELG1001 – Señales y Sistemas

Transformada Fourier – Tabla de Propiedades

30 julio, 201727 diciembre, 2021

Distribución Normal estándar acumulada

Referencia: Gubner 5.1 Table 5.1 p 189

Valores de la función de distribución acumulada normal estandar Φ(x) y su complementaria Q(x)= 1- Φ(x). Para evaluar Φ y Q para argumentos negativos, use el hecho que la densidad normal estándar es par, Φ(-x) = Q(x).

\Phi(x)= \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{x} e^{-t^2 /2} dt

Q(x) = 1- \Phi(x) = \frac{1}{\sqrt{2 \pi}} \int_{x}^{\infty} e^{-t^2 /2} dt

x	Φ(x)	Q(x)	x	Φ(x)	Q(x)
0.0	0.5000	0.5000	2.0	0.9772	0.0228
0.1	0.5398	0.4602	2.1	0.9821	0.0179
0.2	0.5793	0.4207	2.2	0.9861	0.0139
0.3	0.6179	0.3821	2.3	0.9893	0.0107
0.4	0.6554	0.3446	2.4	0.9918	0.0082
0.5	0.6915	0.3085	2.5	0.9938	0.0062
0.6	0.7257	0.2743	2.6	0.9953	0.0047
0.7	0.7580	0.2420	2.7	0.9965	0.0035
0.8	0.7881	0.2119	2.8	0.9974	0.0026
0.9	0.8159	0.1841	2.9	0.9981	0.0019
1.0	0.8413	0.1587	3.0	0.9987	0.0013
1.1	0.8643	0.1357	3.1	0.9990	0.0010
1.2	0.8849	0.1151	3.2	0.9993	0.0007
1.3	0.9032	0.0968	3.3	0.9995	0.0005
1.4	0.9192	0.0808	3.4	0.9997	0.0003
1.5	0.9332	0.0668	3.5	0.9998	0.0002
1.6	0.9452	0.0548	3.6	0.9998	0.0002
1.7	0.9554	0.0446	3.7	0.9999	0.0001
1.8	0.9641	0.0359	3.8	0.9999	0.0001
1.9	0.9713	0.0287	3.9	1.0000	0.0000

30 julio, 201727 diciembre, 2021

Variables Aleatorias Contínuas

Referencia: León-García 445 Important Continuous Random Variables p164

[uniforme] [Exponencial] [Normal] [Gamma] [Erlang m-1] [Chi-cuadrado] [Lapacian] [Rayleigh] [Cauchy] [Pareto] [Beta]

Uniforme

S_X = [a,b]

f_X(x) = \frac{1}{b-a}

a\leq x \leq b

E[X] = \frac{a+b}{2}

VAR[X] = \frac{(b-a)^2}{12}

\Phi_X(\omega) = \frac{e^{j\omega b}- e^{j\omega a}}{j\omega(b-a)}

Exponencial

S_X = [0, \infty)

f_X(x) = \lambda e ^{-\lambda c}

x \geq 0 \text{ , } \lambda > 0

E[X] = \frac{1}{\lambda}

VAR[X] = \frac{1}{\lambda ^2}

\Phi_X(\omega) = \frac{\lambda}{\lambda - j\omega}

Nota: La variable aleatoria exponencial es la única variable aleatoria contínua con propiedad «sin memoria»

Normal o Gausiana

S_X = (-\infty, +\infty)

f_X(x) = \frac{e^{-(x-m)^2 /2 \sigma ^2}}{\sqrt{2 \pi}\sigma}

– ∞ < x < + ∞ , σ >0

E[X] = m

VAR[X] = \sigma ^2

\Phi_X(\omega) = e^{jm\omega - \sigma ^2 \omega ^2 /2}

Nota: En un amplio rango de condiciones, X puede ser usada para aproximar la suma de un gran número de variables aleatorias independientes

Gamma

S_X = (0, \infty)

f_X(x) = \frac{ \lambda (\lambda x)^{\alpha -1} e^{-\lambda x} } {\Gamma(\alpha)}

x > 0, \alpha >0, \lambda > 0

donde  $\Gamma(z)$  es la función gamma:
 $\Gamma(z) = \int_{0}^{\infty} x^{z-1} e^{-x} dx , z>0$ 
 $\Gamma \left(\frac{1}{2} \right) = \sqrt{\pi}$ 
 $\Gamma (z+1) = z \Gamma(z) , z>0$ 
 $\Gamma (m+1) = m! , m>0 \text{, y entero}$

E[x] = \frac{\alpha}{\lambda}

VAR[X] = \frac{\alpha}{\lambda^2}

\Phi_X(\omega) =\frac{1}{(1-j\omega /\lambda)^{\alpha}}

Casos especiales de Gamma
.

Erlang m-1

\alpha = m \text{, entero positivo}

$f_X(x) = \frac{ \lambda e^{-\lambda x }(\lambda x)^{m - 2} } {(m-1)!}$ $x>0$

\Phi_X(\omega) = \left( \frac{1}{1-j\omega /\lambda} \right) ^{m}

Nota: Una variable aleatoria Erlang m-1 se obtiene al añadir m variables aleatorias exponenciales independientes con parámetro λ
.

Chi-cuadrado
con k grados de libertad:

\alpha = k/2 \text{, k entero positivo y } \lambda =1/2

f_X(x) = \frac{ x^{(k - 2)/2} e^{-x/2} } {2^{k/2} \Gamma (k/2)}

x>0

\Phi_X(\omega) = \left( \frac{1}{1-2j\omega} \right) ^{k/2}

Nota: la suma de k variables aleatorias Gausianas, mutuamente independientes, con varianza unitaria, media cuadrada 0, es una variable aleatoria Chi-cuadrada con k grados de libertad.

Lapacian

S_X = (-\infty, +\infty)

f_X(x) = \frac{\alpha}{2} e^{-\alpha|x|}

– ∞ < x < + ∞ , α >0

E[x] =0

VAR[X] = \frac{2}{\alpha^2}

\Phi_X(\omega) = \frac{\alpha^2}{\omega ^2 + \alpha ^2}

Rayleigh

S_X = [0, \infty)

f_X(x) = \frac{x}{\alpha^2} e^{-x^2/2\alpha^2}

x \geq 0 , \alpha>0

E[X] = \alpha \sqrt{\pi/2}

VAR[X] =(2- \pi/2) \alpha^2

Cauchy

S_X = (-\infty, +\infty)

f_X(x) = \frac{\alpha / \pi}{x ^2 + \alpha ^2}

– ∞ < x < + ∞ , α >0

NO existe la media o varianza

\Phi_X(\omega) = e^{-\alpha|\omega| }

Pareto

S_X = [X_m, +\infty) , X_m>0

f_X(x) = \begin{cases} 0 && x< x_m\\ \alpha \frac{x_m^{\alpha}}{x^{\alpha+1}} && x \geq x_m \end{cases}

E[X] =\frac{\alpha x_m}{\alpha - 1}, \alpha >1

VAR[X] =\frac{\alpha x_m^2}{(\alpha - 2)(\alpha-1)^2}, \alpha >2

Nota: La variable aleatoria Pareto es el ejemplo mas destacado de variables aleatorias con colas largas y puede ser vista como una versión contínua de la variable aleatoria discreta Zipf

Beta

f_X(x) = \begin{cases} \frac{\Gamma (\alpha + \beta)}{\Gamma(\alpha) \Gamma(\beta)} x^{\alpha-1} (1-x)^{\beta-1} && ,\alpha>0 \\, && \beta>0 \\ , && 0 < x < 1 \\ 0 && \text{otro caso} \end{cases}

E[X] = \frac{\alpha}{\alpha + \beta}

VAR[X] = \frac{\alpha\beta}{(\alpha + \beta)^2 (\alpha + \beta + 1)}

Nota: La variable aleatoria Beta es util para modelar una variedad de formas de funciones de densidad de probabilidad en intervalos finitos

[uniforme] [Exponencial] [Normal] [Gamma] [Erlang m-1] [Chi-cuadrado] [Lapacian] [Rayleigh] [Cauchy] [Pareto] [Beta]

30 julio, 201727 diciembre, 2021

Variables Aleatorias Discretas

Referencia: León-García 3.5 Important Discrete Random Variables p115

[Bernoulli] [Binomial] [Geométrica] [Binomial Negativa] [Poisson] [Uniforme] [Zipf]

Bernoulli

S_X=\{0, 1 \}

p_0 = q = 1-p

p_1=p, 0 \leq p \leq 1

E[X] = p

VAR[x] = p(1-p)

G_X(z)=(q+pz)

Nota: La variable aleatoria Bernoulli es es valor de la función indicador I_A para algún evento; X=1 si ocurre A, y 0 en otro caso

Binomial

S_X=\{0, 1, ... , n \}

p_k={n \choose k} p^{k} (1-p)^{n-k}

k = 0, 1, ... , n

E[X]= np

VAR[X] = np(1-p)

G_X(z)= (q + pz)^{n}

Nota: X es el numero de éxtidos en n intentos Bernoulli y por consiguiente la suma de n iid variables aleatorias Bernoulli.

Geométrica

Versión 1:

S_X=\{0, 1, 2, ... \}

p_k = p(1-p)^{k}

k= 0, 1, , ...

E[X] =\frac{1-p}{p}

VAR[X] = \frac{1-p}{p^2}

G_X(z) = \frac{p}{1-qz}

Nota: X es el número de fallas antes del primer éxito en una secuencia de intentos Bernoulli independientes. La variable aleatoria geométrica es la única una variable aleatoria con propiedad «sin memoria».

Versión 2:

S_X'=\{ 1, 2, ... \}

p_k = p(1-p)^{k-1}

k= 1, 2, ...

E[X'] =\frac{1}{p}

VAR[X'] = \frac{1-p}{p^2}

G_{X'}(z) = \frac{pz}{1-qz}

Nota: X’= X+1 es el número de intentos hasta primer éxito en una secuencia de intentos Bernoulli independientes.

Binomial Negativa

S_X=\{ r, r+1, ... \}

, donde r es un entero positivo

p_k = {{k-1} \choose {r-1}} p^{r}(1-p)^{k-r}

k = r, r+1, ...

E[x] = \frac{r}{p}

VAR[X] = \frac{r(1-p)}{p^2}

G_X(z) = \left( \frac{pz}{1-qz}\right)^{r}

Nota: X es el número de intentos hasta el r-ésimo éxito en una secuencia de intentos Bernoulli independientes

Poisson

S_X=\{0, 1, 2, ... \}

p_k = \frac{\alpha ^{k}}{k!} e^{-\alpha}

k = 0, 1, ... \text{ y } \alpha>0

E[X] = \alpha

VAR[X] = \alpha

G_X(z) = e^{\alpha(z-1)}

Nota: X es el número de eventos que ocurren en una unidad de tiempo cuando el tiempo entre eventos es distribuido exponencialmente con media 1/α.

Uniforme

S_X=\{1, 2, ..., L \}

p_k = \frac{1}{L}

k = 1, 2, ... , L

E[X] = \frac{L+1}{2}

VAR[X] = \frac{L^2 -1}{12}

G_X(z) = \frac{z}{L} \frac{1- z^L}{1-z}

Nota: La variable aleatoria uniforme sus resultados son igualmente probables. Juega un rol importante en la generación de números aleatorios

Zipf

S_X=\{1, 2, ..., L \}

, donde L es un entero positivo

p_k = \frac{1}{c_L} \frac{1}{k}

k = 1, 2, ... , L

donde c_L esta dado por:

c_L = \sum_{j=1}^{L} = 1 + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{L}

E[X] =\frac{L}{c_L}

VAR[X] = \frac{L(L+1)}{2C_L} - \frac{L^2}{c_L ^2}

Nota: La variable aleatoria Zipf tiene la propiedad que algunos resultados ocurren frecuentemente, pero muchos resultados suceden muy poco

[Bernoulli] [Binomial] [Geométrica] [Binomial Negativa] [Poisson] [Uniforme] [Zipf]

15 julio, 201727 diciembre, 2021

Expansiones de Series

Referencia: Leon W Couch Apéndice p658

Series Finitas

\sum_{n=1}^{N} n = \frac{N(N+1)}{2}

\sum_{n=1}^{N} n^2 = \frac{N(N+1)(2N+1)}{6}

\sum_{n=1}^{N} n^3 = \frac{N^2(N+1)^2}{4}

\sum_{n=0}^{N} a^n = \frac{a^{N+1}-1}{a-1}

\sum_{n=0}^{N} \frac{N!}{n!(N-n)!}x^n y^{N-n} = (x+y)^N

\sum_{n=0}^{N} e^{j(\theta+n\phi)} = \frac{sen \left[(N+1) \frac{\phi}{2}\right] }{sen \left( \frac{\phi}{2} \right)} e^{j [ \theta + \left( N \frac{\phi}{2} \right) ]}

\sum_{n=0}^{N} {N \choose k} a^{N-k}b^{k} = (a+b)^N,

donde: {N \choose k} = \frac{N!}{(N-k)!k!}

Series Infinitas

Serie de Taylor

f(x) = \sum_{n=0}^{\infty} \left( \frac{f^{(n)}(a)}{n!} \right) (x-a)^n

Serie de Fourier

f(x) = \sum_{n=-\infty}^{\infty} c_n e^{jn\omega_0 x}

a\leq x \leq (a+T)

donde: c_n = \frac{1}{T} \int_{a}^{a+T} f(x) e^{-jn\omega_0 x} dx

\omega_o = \frac{2\pi}{T}

otras series

e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!}

sen(x) = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{(2n+1)!}

cos(x) = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n}}{(2n)!}

15 julio, 201727 diciembre, 2021

Tabla de Integrales Definidas

Referencia: Leon W Couch Apéndice p657, 658

Integrales Definidas

Definición

\int f(x) dx = \lim_{\Delta \rightarrow 0} \left( \sum_{n} \left[ f(n \Delta x)\right] \Delta x \right)

Cambio de variable. Sea v=u(x)

\int_{a}^{b} f(x) dx = \int_{u(a)}^{u(b)} \left( \left. \frac{f(x)}{dv/dx} \right|_{x=u^{-1}(v)}\right) dv

integración por partes

\int u dv = uv - \int v du

Integrales Definidas

\int_{0}^{\infty} \frac{x^{m-1}}{1+x^n} dx = \frac{\pi /n}{sen(m\pi/n)}, \text{ }n>m>0

\int_{0}^{\infty} x^{\alpha-1}e^{-x} dx = \Gamma(\alpha) , \alpha > 0

\text{donde: }\Gamma(\alpha +1) = \alpha \Gamma(\alpha),

\Gamma (1) = 1,

\Gamma [1/2] = \sqrt{\pi},

\Gamma(n) = (n-1)! \text{, si n es entero positivo }

\int_{0}^{\infty} x^{2n} e^{-ax^2} dx =\frac{1 \cdot 3 \cdot 5 \cdot \cdot \cdot (2n-1)}{2^{n+1}a^{n}} \sqrt{\frac{\pi}{a}}

\int_{-\infty}^{\infty} e^{-a^2 x^2 + bx} dx =\frac{\sqrt{\pi}}{a} e^{b^2/(4a^2)}, a>0

\int_{0}^{\infty} e^{-ax}cos(bx) dx = \frac{a}{a^2+b^2}, a>0

\int_{0}^{\infty} e^{-ax}sen(bx) dx = \frac{b}{a^2+b^2}, a>0

\int_{0}^{\infty} e^{-a^2x^2}cos(bx) dx = \frac{\sqrt{\pi} e^{-b^2/4a^2}}{2a}, a>0

\int_{0}^{\infty} x^{\alpha-1}cos(bx) dx =

\frac{\Gamma(\alpha)}{b^{\alpha}} cos \left(\frac{1}{2}\pi \alpha \right),

0<\alpha < 1, b >0

\int_{0}^{\infty} x^{\alpha-1}sen(bx) dx = \frac{\Gamma(\alpha)}{b^{\alpha}} sen \left(\frac{1}{2}\pi \alpha \right),

0<|\alpha| < 1, b >0

\int_{0}^{\infty} x e^{-ax^2} I_k(bx) dx = \frac{1}{2a} e^{b^2/4a},

\text{donde: } I_k(bx)=\frac{1}{\pi}\int_{0}^{\pi} e^{bx cos(\theta)} cos(k\theta) d\theta

\int_{0}^{\infty} \frac{sen(x)}{x} dx = \int_{0}^{\infty} Sa(x) dx = \frac{\pi}{2}

\int_{0}^{\infty} \left( \frac{sen(x)}{x} \right)^2 dx = \int_{0}^{\infty} Sa^2(x) dx = \frac{\pi}{2}

\int_{-\infty}^{\infty} e^{\pm j2 \pi yx} dx = \delta (y)

\int_{0}^{\infty}\frac{cos(ax)}{b^2 + x^2}dx = \frac{\pi}{2b} e^{-ab}, a>0,b>0

\int_{0}^{\infty}\frac{x sen(ax)}{b^2 + x^2}dx = \frac{\pi}{2} e^{-ab}, a>0,b>0

15 julio, 201727 diciembre, 2021

Tabla de Integrales Indefinidas

Referencia: Leon W Couch Apéndice p656

Integrales Indefinidas

\int (a+bx)^n dx = \frac{(a+bx)^{n+1}} {b(n+1)}, 0<n

\int \frac{dx}{a+bx} =\frac{1}{b} ln|a+bx|

\int \frac{dx}{(a+bx)^n} = \frac{-1}{(n-1)b(a+bx)^{n-1}} , 1<n

\int \frac{dx}{(c+bc+ax^2)^n} =

= \begin{cases} \frac{2}{ \sqrt{4ac-b^2}} tan^{-1}\left(\frac{2ax+b}{\sqrt{4ac-b^2}}\right) , & b^{2} < 4ac \\ \frac{1}{\sqrt{b^2-4ac}}ln\left| \frac{2ax+b-\sqrt{b^2-4ac}}{2ax+b+\sqrt{b^2-4ac}} \right| , & b^{2} > 4ac \\ \frac{-2}{\sqrt{2ax+b}} , & b^{2}=4ac \end{cases}

\int \frac{x dx}{c+bx+ax^2} =

= \frac{1}{2a} ln\left| ax^2+bx+c \right| - \frac{b}{2a}\int \frac{dx}{c+bx+ax^2}

\int \frac{dx}{a^2+b^2x^2} = \frac{1}{ab} tan^{-1}\left( \frac{bx}{a} \right)

\int \frac{x dx}{a^2+x^2} = \frac{1}{2} ln( a^2+x^2 )

Trigonométricas

\int cos(x) dx = sen(x)

\int sen(x) dx = -cos(x)

\int x cos(x) dx = cos(x) + x sen(x)

\int x sen(x) dx = sen(x) - x cos(x)

\int x^2 cos(x) dx = 2x cos(x) + (x^2 -2) sen(x)

\int x^2 sen(x) dx = 2x sen(x) - (x^2 -2) cos(x)

Exponenciales

\int e^{ax} dx = \frac{e^{ax}}{a}

\int x e^{ax} dx = e^{ax} \left( \frac{x}{a} - \frac{1}{a^2} \right)

\int x^2 e^{ax} dx = e^{ax} \left( \frac{x^2}{a} - \frac{2x}{a^2} + \frac{2}{a^3} \right)

\int x^3 e^{ax} dx = e^{ax} \left( \frac{x^3}{a} - \frac{3x^2}{a^2} + \frac{6x}{a^3} - \frac{6}{a^4}\right)

\int e^{ax} sen(x) dx = \frac{e^{ax}}{a^2 +1} (a sen(x) - cos(x))

\int e^{ax} cos(x) dx = \frac{e^{ax}}{a^2 +1} (a cos(x) - sen(x))

15 julio, 201727 diciembre, 2021

Tabla de Números Complejos

Referencia: Leon W Couch Apéndice p653

Definiciones

sen(x) = \frac{e^{jx}-e^{-jx}}{2j}

cos(x) = \frac{e^{jx}+e^{-jx}}{2}

tan(x) = \frac{sen(x)}{cos(x)}= \frac{e^{jx}-e^{-jx}}{j(e^{jx}+e^{-jx})}

Teorema de Euler

e^{\pm jx} = cos(x) \pm j sen(x)

Complejos

e^{\pm j\pi /2} = \pm j

e^{\pm jn\pi} = \begin {cases} 1 \text{, n par} \\ -1 \text{, n impar}\end{cases}

forma rectangular

x + jy = Re^{j\theta}

R = \sqrt{ x^2 + y^2}

\theta = tab^{-1}\left( \frac{y}{x} \right)

a una potencia

\left( R e^{j\theta} \right)^y = R^y e^{jy\theta}

\left( R_1 e^{j\theta_1} \right) \left( R_2 e^{j\theta_2} \right) = R_1 R_2 ^{j(\theta_1+\theta_2)}

15 julio, 201727 diciembre, 2021

Tablas trigonométricas

Referencia: Leon W Couch Apéndice p653

cos(x \pm y)= cos(x)cos(y) \mp sen(x)sen(y)

sen(x \pm y) = sen(x)cos(y) \pm cos(x) sen(y)

cos\left( x \pm \frac{\pi}{2}\right) = \mp sen(x)

sen\left( x \pm \frac{\pi}{2}\right) = \pm cos(x)

cos(2x)= cos^2 (x)- sen^2(x)

sen(2x)= 2sen(x)cos(x)

2 cos(x)cos(y) = cos(x-y) + cos(x+y)

2 sen(x)sen(y) = cos(x-y) - cos(x+y)

2 sen(x)cos(y) = sen(x-y) + sen(x+y)

2 cos^2(x) = 1 + cos(2x)

2 sen^2(x) = 1 - cos(2x)

4 cos^3(x) = 3cos(x) + cos(3x)

4 sen^3(x) = 3sen(x) + sen(3x)

8 cos^4(x) = 3 + 4cos(2x) + cos(4x)

8 sen^4(x) = 3 - 4cos(2x) + cos(4x)

con magnitud R y fase Θ

R cos(x + \theta) = A cos(x) - B sen(x)

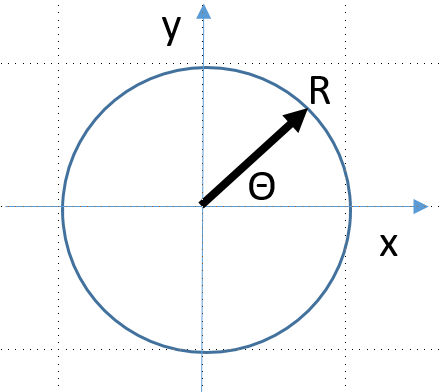
donde

R = \sqrt{A^2+B^2}

\theta = tan^{-1}(\frac{B}{A})

A = R cos(\theta)

B = R sen(\theta)

15 julio, 201727 diciembre, 2021

Tabla de derivadas

Referencia: Leon W Couch Apéndice p656

Tabla de Derivadas

Definición

\frac{d}{dx}[ f(x) ]= \lim_{\Delta x \rightarrow\ 0} \frac{f \big( x+\frac{\Delta x}{2} \big)- f\big( x-\frac{\Delta x}{2}\big) }{\Delta x}

Regla del producto

\frac{d}{dx}[u(x) v(x)]= u(x)\frac{dv(x)}{dx} + v(x)\frac{du(x)}{dx}

Regla del cociente

\frac{d}{dx} \left[ \frac{u(x)}{v(x)}\right] = \frac{1}{v^2(x)} \left[ v(x)\frac{du(x)}{dx}- u(x)\frac{dv(x)}{dx}\right]

Regla de la cadena

\frac{d}{dx}u[v(x)]= \frac{du}{dv}\frac{dv}{dx}

Potenciación

\frac{d}{dx}[ x^n ]= nx^{n-1}

Exponenciales

\frac{d}{dx} [ e ^{ax} ] = a e^{ax}

\frac{d}{dx} [ a ^{x} ]= a^x ln(a)

Logaritmicas

\frac{d}{dx} [ ln(x) ] = \frac{1}{x}

\frac{d}{dx}[ log_a (x) ] = \frac{1}{x} log_a e

Trigonométricas

\frac{d}{dx}[sen(ax)]= a\text{ } cos(ax)

\frac{d}{dx}[cos(ax)]= -a\text{ }sen(ax)

\frac{d}{dx}[tan(ax)]= \frac{a} {cos^2(ax)}

\frac{d}{dx}[sen^{-1}(ax)]= \frac{a} {\sqrt{1-(ax)^2}}

\frac{d}{dx}[cos^{-1}(ax)]= \frac{-a} {\sqrt{1-(ax)^2}}

\frac{d}{dx}[tan^{-1}(ax)]= \frac{a} {{1+(ax)^2}}

Regla de Leibniz

$\frac{d}{dx}\left[ \int_{a(x)}^{b(x)} f(\lambda,x) d\lambda \right] =$
$= f(b(x),x) \frac{d}{dx}[b(x)] - f(a(x),x) \frac{d}{dx}[a(x)] +$
$+ \int_{a(x)}^{b(x)} \frac{d}{dx}[f(\lambda , x) d\lambda$