Categoría: Soluciones

Referencia: Problema 9.13 Leon-García p.558 pdf 55

El proceso aleatorio Z(t) definido por:

Z(t) = 2Xt –Y

donde X y Y son  variables aleatorias con medias m_X, m_Y ,  varianzas σ²_X y σ²_Y y coeficientes de correlación ρ_XY.

Encuentre la media y autocovarianza de Z(t)

---

Solución propuesta:

E[Z(t)] = E[ 2Xt - Y ]
    = 2E[X]t - E[Y]
    = 2tmX - mY = mZ

CZ(t1, t2) = E[(2Xt1 - Y)(2Xt2 - Y)] - mZ(t1) mZ(t2)
    = E[ 4X2 t1t2 - 2XYt1   - 2XYt2 + Y2] 
      - (2t1mX - mY)(2t2mX - mY)
    = 4t1t2 E[X2] - 2t1 E[XY] - 2t2 E[XY] + E[Y2] 
      - (4t1t2m2X -2t1mXmY -2t2mXmY + m2Y)
    = 4t1t2 E[X2] - 2(t1 +t2)E[XY] + E[Y2] 
      -4t1t2m2X + 2(t1+2)mXmY - m2Y 
    = 4t1t2 (E[X2] - m2X ) - 2(t1 +t2)(E[XY] - mXmY) + (E[Y2] - m2Y)
    = 4t1t2 σ2X - 2(t1 +t2)σXY + σ2Y 

dado ρXY = σXY/σXσY
     ρXYσXσY = σXY

    = 4t1t2 σ2X - 2(t1 +t2) ρXYσXσY  + σ2Y 

σ2Z(t) = CZ(t, t) = 4t2σ2X - 4t ρXYσXσY + σ2Y 

Para X y Y solo se da la media y varianza, la función final debe tener la misma forma:
f_{Z(t)} = \frac{e^{ -(z - m_Z)^2 /(2 \sigma_Z^2)}}{ \sqrt{2 \pi }\sigma_Z}

f_{Z(t)} = \frac{e^{-\frac{(z - 2t m_{X} +m_{Y})^2 }{(2(4t^2\sigma_{X}^2 - 4t\sigma_{X} \sigma_{Y} \rho_{XY} + \sigma_{Y}^2)}}}{ \sqrt{2 \pi }\sqrt{4t^2\sigma_{X}^2 - 4t\sigma_{X} \sigma_{Y} \rho_{XY} + \sigma_{Y}^2}}

1Eva_IIT2017_T4 Multiplexor conexiones dos tipos – colas

a) Determine el espacio de estados del sistema

"Para los estados utilice la nomenclatura (tp1, tp2), donde tpi corresponde a la cantidad de atención de enlaces tipo i."
Para el caso que λ1>sea positivo y λ2=0
s1 = {00, 10, 20, 30, 40, 50}

Para el caso que λ1=0 y λ2 es positivo
s2 = {01, 02}

Se completan los casos intermedios para usar toda la capacidad
sotros = {11, 12, 21, 31}

El total de Espacios de estados será la union de los tres espacios anteriores:
s = {00, 10, 20, 30, 40, 50, 01, 02, 11, 12, 21,31}

b) Dibuje y etiquete el diagrama de estados del sistema

c) Plantee las ecuaciones de estados del sistema

SALE = ENTRA
Primera Fila del diagrama
(λ1 +λ2     ) p00 =  µ1p10 + µ2p01
(λ1 +λ2 + µ1) p10 = 2µ1p20 + µ2p11 +λ1p00 
(λ1 +λ2 +2µ1) p20 = 3µ1p30 + µ2p21 +λ1p10 
(λ1 +λ2 +3µ1) p30 = 4µ1p40 + µ2p31 +λ1p20 
(λ1     +4µ1) p40 = 5µ1p40 +      +λ1p30 
         5µ1  p50 =  λ1p40 
Segunda Fila del diagrama
(λ1 +λ2 + µ2    ) p01 =  µ1p11 + 2µ2p02       +λ2p00 
(λ1 +λ2 + µ1 +µ2) p11 = 2µ1p21 + 2µ2p12 +λ1p01 +λ2p10 
(λ1     +2µ1 +µ2) p21 = 3µ1p31         +λ1p11 +λ2p20 
(       +3µ1 +µ2) p31 =               +λ1p21 +λ2p30 
Tercera Fila del diagrama
(λ1 +2µ2) p02 =  µ1p12 +λ2p01 
(µ1 +2µ2) p12 =  λ1p02 +λ2p11 

p00 +p10 +p20 +p30 +p40 +p50 +p01 +p11 +p21 +p31 +p02 +p12 =1 

d) Determine la probabilidad de pérdidas de conexiones tipo 1 y tipo 2, y la probabilidad de pérdidas del sistema.

Pérdidas de tipo 1 se dan en los estados 12, 31, 50
ptipo1 = p12 + p31 + p50

Pérdidas de tipo 2 se dan en los estados 12, 31, 50, 02, 21, 40
ptipo2 = p12 + p31 + p50 + p02 + p21 + p40

e) ¿Cuál probabilidad de pérdidas es más alta? Para conexiones tipo 1 o 2, describa su respuesta.

Se pierden más conexiones del tipo 2, pues existen más términos en la suma de probabilidades

f) Calcule la utilización del enlace por cada tipo

Se calcula como valor esperado por ocupación de servidores:

\rho = \frac{\sum_{i=0}^{5} \sum_{j=0}^{3} p_{ij} (i \text{1MB} + j \text{2MB})}{\text{5MB}}

En el caso que se requieren por tipo de conexión:
\rho_{1} = \frac{\sum_{i=0}^{5} \sum_{j=0}^{3} p_{ij} (i \text{1MB} )}{\text{5MB}}
\rho_{2} = \frac{\sum_{i=0}^{5} \sum_{j=0}^{3} p_{ij} (j \text{2MB})}{\text{5MB}}

1Eva_IIT2017_T3 Multiplexor-Colas

a) Determine el espacio de estados del sistema

S={0,1,2,3,4,5,6}

b) Dibuje y etiquete el diagrama de estados del sistema

c) Calcule las probabilidades de cada estado (PMF)

SALE = ENTRA
(1) λp0 = µp1
(2) (λ + µ)p1 = λp0 + 2µp2
(3) (λ + 2µ)p2 = λp1 + 3µp3
(4) (λ + 3µ)p3 = λp2 + 4µp4
(5) (λ + 4µ)p4 = λp3 + 5µp5
(6) 5µp5 = λp4
(7) p0 + p1 + p2 + p3 + p4 + p5 = 1

(1) p1 = (λ/µ) p0 

(2) (λ + µ)(λ/µ) p0  = λp0 + 2µp2 
    p2 = [1/2µ] [(λ + µ)(λ/µ) - λ] p0 
    p2 = [λ/2µ2] [(λ + µ) - µ] p0 
    p2 = (1/2)(λ/µ)2 p0 

(3) (λ + 2µ)p2 = λp1 + 3µp3 
    (λ + 2µ)(1/2)(λ/µ)2 p0  = λ (λ/µ) p0  + 3µp3 
    [(λ + 2µ)(1/2)(λ/µ)2 - (λ2/µ)] p0  = + 3µp3 
    3µp3 = (λ/µ)2 [(1/2)(λ + 2µ) - µ ] p0 
    p3 = (1/3µ)(λ/µ)2 (λ + 2µ - 2µ)/2 p0 
    p3 = [1/(2*3)](λ/µ)2 (λ/µ) p0 
    p3 = (1/3!)(λ/µ)3 p0

(4) (λ + 3µ)(1/(2*3))(λ/µ)3 p0 = λ(1/2)(λ/µ)2 p0  + 4µp4
    4µp4  = [(λ + 3µ)(1/(2*3))(λ/µ)3 - λ(1/2)(λ/µ)2] p0 
    4µp4  = (1/2)(λ/µ)3[(1/3)(λ + 3µ) - µ] p0 
    p4  = [1/2*4µ](λ/µ)3((λ + 3µ) - 3µ)/3 p0 
    p4  = [1/2*3*4](λ/µ)3(λ/µ) p0 
    p4  = (1/4!)(λ/µ)4 p0 

(5) (λ + 4µ)(1/4!)(λ/µ)4 p0  = λ(1/3!)(λ/µ)3 p0 + 5µp5
     5µp5 = [(λ + 4µ)(1/4!)(λ/µ)4 - λ(1/3!)(λ/µ)3] p0 
     5µp5 = [(1/4!)(λ/µ)4][(λ + 4µ-  4µ] p0
     p5 = (1/5!)(λ/µ)5 p0 

(7) p0 + (λ/µ) p0 + (1/2)(λ/µ)2 p0 + [1/3!](λ/µ)3 p0 + (1/4!)(λ/µ)4 p0  + (1/5!)(λ/µ)5 p0 = 1
    p0 [1 + (λ/µ) + (1/2)(λ/µ)2 + (1/3!)(λ/µ)3 + (1/4!)(λ/µ)4 + (1/5!)(λ/µ)5 ] = 1
    p0  = 1/ [1 + (λ/µ) + (1/2)(λ/µ)2 + (1/3!)(λ/µ)3 + (1/4!)(λ/µ)4 + (1/5!)(λ/µ)5 ]

d) Encuentre la probabilidad de pérdidas de conexiones.

p5 =  (1/5!)(λ/µ)5 p0  
   = (1/5!)(λ/µ)5 /  [1 + (λ/µ) + (1/2)(λ/µ)2 + (1/3!)(λ/µ)3 + (1/4!)(λ/µ)4 + (1/5!)(λ/µ)5 ]

e) ¿Cuál es el factor de utilización del enlace?

Es el valor esperado de uso de capacidad relativo a la capacidad máxima del multiplexor.

\rho = \frac{\sum_{i=0}^{5}(i)(p_i )\text{1MB}}{\text{5MB}}

Ejercicio: 1Eva_IIT2017_T2 Radio-enlaces con Markov

Para un radio-enlace realice un modelo con una Cadena de Markov:

a) Determine el espacio de estados
s={0,1}

b) Realice el diagrama de estados, etiquete claramente

c) Escriba la matriz de transición y calcule la probabilidad de estado estable.
\begin{bmatrix} (1-\alpha) & \alpha\\ \beta & (1-\beta) \end{bmatrix}

(1-α) π0 +     β π1 = π0
    α π0 + (1-β) π1 = π1
      π0 +       π1 = 1

[(1-α)-1) π0 +         β π1 = 0
        α π0 + [(1-β)-1] π1 = 0
          π0 +            π1 = 1

Se seleccionan dos ecuaciones incluyento la suma de probabilidades es 1:

-α π0 + β π1 = 0
 α π0 - β π1 = 0
   π0 + π1 = 1

β π1 = α π0 
 π1 = α/β π0 

π0 + α/β π0 = 1
(1 + α/β)π0 = 1

π0 = β/(β + α)
π1 = α/(β + α)

Suponga que α=0.01, β=0.02 y determine para todo el enlace entre las ciudades:

d) La matriz de transición entre las ciudades A y B

p^{(3)}=\begin{bmatrix} 0.99 & 0.01\\ 0.02 & 0.98 \end{bmatrix}^{3}

p = [[0.99, 0.01],
     [0.02, 0.98]]
>>> p2 = np.linalg.matrix_power(p,2)
p2 = [[ 0.9803  0.0197]
      [ 0.0394  0.9606]]
>>> p3 = np.linalg.matrix_power(p,3)
p3 = [[ 0.970891  0.029109]
      [ 0.058218  0.941782]]

e) Probabilidad de error para un dígito binario 0 (bit)
P₀₁ = 0.029109

f) Probabilidad de error para un bit con valor 1 (bit)
P₁₀ = 0.058218

g) El error al transmitir un bit en todo el enlace
P₀₁ + P₁₀ = 0.029109 + 0.058218 = 0.0873

h) Observe y comente sus resultados
El sistema es semejante a usar una matriz de probabilidad para un sistema durante tres periodos de tiempo.
Las probabilidades se interpretan desde la matriz. Mientras más tramos se avanza en los radioenlaces, la probabilidad de falla aumenta, proporcional a los factores α y β.

1Eva_IIT2017_T1 Código Morse con Markov

a) Determine el espacio de estados
s={0,1,2} = {'.- '}

b) Realice el diagrama de estados

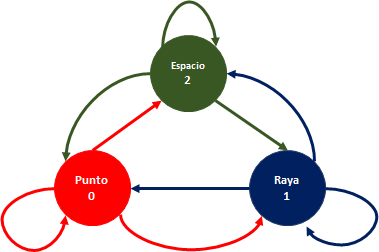
c) Escriba la matriz de transición y ubique los valores encontrados en el diagrama.

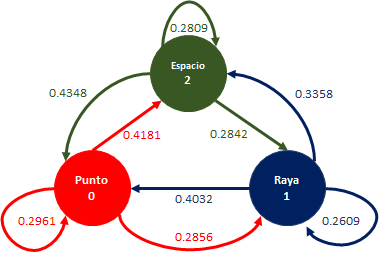
d) Calcule la probabilidad de estado estable o largo plazo.

Ecuaciones:

0,2961 π0 + 0,4032 π1 + 0,4348 π2 = π0
0,2856 π0 + 0,2609 π1 + 0,2842 π2 = π1
0,4181 π0 + 0,3358 π1 + 0,2809 π2 = π2
π0 + π1 + π2 = 1

Tomando 3 ecuaciones, siempre usando que la suma de probabilidades es 1

(0,2961-1) π0 + 0,4032 π1 + 0,4348 π2 = 0
0,2856 π0 + (0,2609-1) π1 + 0,2842 π2 = 0
0,4181 π0 + 0,3358 π1 + (0,2809-1) π2 = 0
π0 + π1 + π2 = 1

-0,703817809	0,403205408	0,434822831		0
0,285650584	-0,73908635	0,284203177		0
0,418167225	0,335880942	-0,719026008		0
       1	       1	       1		1

       1	       1	       1		1
0,285650584	-0,73908635	0,284203177		0
0,418167225	0,335880942	-0,719026008		0

 1	       1	       1		1
0	3,587379095	0,005067055		1
0	0,196778413	2,719470024		1

1	1	1		   1
0	1	0,001412467	0,278755039
0	0	1		0,347583767

1	0	0		0,3742
0	1	0		0,2783
0	0	1		0,3476

π = [0,3742  0,2783  0,3476]

π₀ = 0,3742
π₁ = 0,2783
π₂ = 0,3476

---

Usando Python:

la suma de filas es: 
[123343  91720 114580]
la matriz de transición es: 
[[ 0.29618219  0.28565058  0.41816722]
 [ 0.40320541  0.26091365  0.33588094]
 [ 0.43482283  0.28420318  0.28097399]]
en estado estable o largo plazo: 
[[ 0.37415214  0.27826409  0.34758377]
 [ 0.37415214  0.27826409  0.34758377]
 [ 0.37415214  0.27826409  0.34758377]]
>>> 

# 1ra Evaluación II Término 2017
# Tema 1. Código Morse-Cadena Markov
import numpy as np
# Ingreso
conteo = np.array([[36532, 35233, 51578],
                   [36982, 23931, 30807],
                   [49822, 32564, 32194]])
# Procedimiento
n = len(conteo)
p = np.zeros(shape=(n,n),dtype=float)

sumafila = np.sum(conteo, axis=1)
for f in range(0,n,1):
    p[f] = conteo[f,:]/sumafila[f]

k=50
pn = np.linalg.matrix_power(p,k)

# Salida
print('la suma de filas es: ')
print(sumafila)
print('la matriz de transición es: ')
print(p)
print('en estado estable o largo plazo: ')
print(pn)