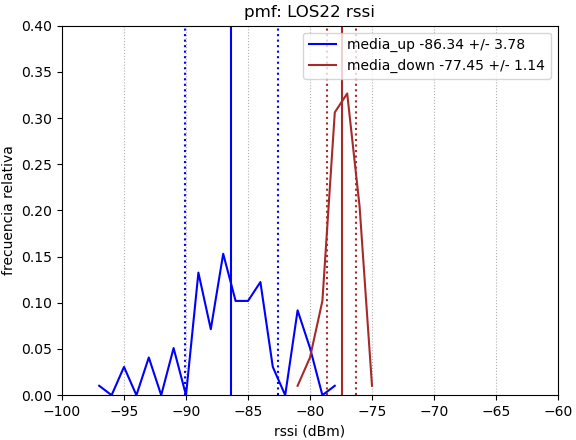
Referencia: León-García p.104, Gubner p.80,
Para describir el comportamiento de una variable aleatoria discreta a partir de su funciones de distribución de probabilidad (pmf, probability mass function), para simplificar en un solo valor, se usa el valor esperado o media.
El valor esperado o media de una variable aleatoria discreta X se define como:
m_x = E[X] = \sum\limits_{x \in S_x} x p_x(x) =
= \sum\limits_{k} x_k p_x(x_k)
El valor esperado E[X] está definido si la suma anterior absolutamente converge , es decir:
E[|X|] = \sum\limits_{k} |x_k| p_x(x_k) < \infty
Ejemplo
De repetir un experimento 150 veces, se obtienen dos variables aleatorias.
- La variable Y tiene valores alrededor de 0,
- mientras que la variable X tiene valores alrededor de 6 .
- También observe que X tiene mayor variación que Y.
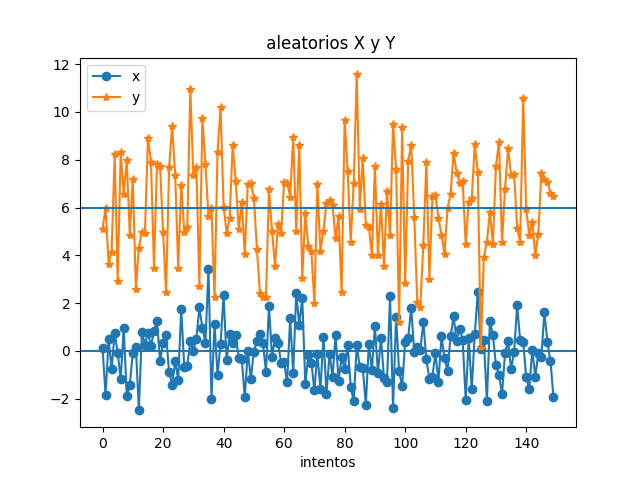
Siendo px(x) la función de distribución de probabilidad de los puntos x1, x2, … , entonces E[x] representa el centro de masa de la distribución.
Ejemplo: Media de una variable aleatoria tipo Bernoulli
(Ejemplo 3.11) Encuentre el valor de la variable aleatoria IA:
E[I_A] = 0p_i(0) + 1p_1(1) = p
donde p es la probabilidad de éxito de una prueba Bernoulli.
Ejemplo: Tres lanzamientos de una moneda y la variable aleatoria Binomial
(Ejemplo 3.12)Sea X el número de caras en tres lanzamientos de una moneda, Encuentre E[X]
E[X] = \sum \limits_{k=0}^{3} k p_x(k)
las probabilidades de que salgan 0 caras es 1/8, 1 cara es 3/8, 2 caras 3/8 y 3 caras 1/8, resultados obtenidos en el ejemplo 3.5 del libro
= 0 \big( \frac{1}{8} \big) + 1 \big(\frac{3}{8} \big) + 2\big(\frac{3}{8} \big) + 3\big(\frac{1}{8} \big)
= \frac{12}{8} =1.5
Ejemplo: Media de una variable aleatoria uniforme
Se conoce que px(j) = 1/M, para j=0, … , M-1, entonces:
E[X] = \sum \limits_{k=0}^{M-1} k \frac{1}{M}
=\frac{1}{M}[ { 0 + 1 + 2 + ... + M-1}]
= \frac{(M-1)M}{2M} = \frac{M-1}{2}
El término de «valor esperado» no quiere decir que esperamos observar E[X] cuando se ejecuta un experimento que genera X.
Por ejemplo, el valor esperado de un intento Bernoulli es p, pero sus resultados siempre son 0 ó 1.
E[X] corresponde al «promedio de X» en un gran número de observaciones de X.
El promedio aritmético o media muestral de las observaciones cuando el número de muestras n tiende a ser grande converge al valor esperado:
\langle X\rangle_n = \sum\limits_{k} x_k f_k(n) \rightarrow
\rightarrow \sum\limits_{k} x_k p_x (x_k) = E[x]
Instrucciones en Python
Para generar valores aleatorios con media y escala conocida se puede usar la función stats.norm.rvs(media, escala, muestras, obteniendo algunos valores como:
px:
[-1 0 -1 -2 3 0 -1 0 0 0 1 0 0 0 0 0 1 1 -1 0 0 -1 0 0
0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
...]
py:
[ 8 4 6 6 2 5 2 3 6 6 7 6 4 5 2 6 4 4 6 7 7 4 4 5
5 4 4 3 2 9 5 8 5 6 7 2 4 1 1 6 5 7 6 7 4 7 9 5
...]
# Valor Esperado E[x] a partir de pmf
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# INGRESO
n = 150
media_x = 0
escala_x = 1
media_y = 6
escala_y = 2
# PROCEDIMIENTO
px = stats.norm.rvs(media_x,escala_x,size=n)
px = np.array(px,dtype=int)
py = stats.norm.rvs(media_y,escala_y,size=n)
py = np.array(py,dtype=int)
# SALIDA
print('px: ')
print(px)
print('py: ')
print(py)
# grafica
plt.title(' aleatorios X y Y')
plt.plot(px, 'o-', label='x')
plt.plot(py, '*-', label='y')
plt.xlabel('intentos')
plt.axhline(media_x)
plt.axhline(media_y)
plt.legend()
plt.show()