Referencia: Ross 8.2 p334
De una estación meteorológica se obtiene un archivo.csv con los datos de los sensores disponibles.

Nota: las instrucciones para la lectura del archivo se describen en:
Archivos.csv con Python – Ejercicio con gráfica de temperatura y Humedad
Para observar la correlación entre las medidas obtenidas de varios sensores, se considera usar las variables:
sensor_EM = ["TEMP","Humidity","Solar_rad","Bar_press."]
La correlación entre las variables se realiza seleccionando las columnas desde una lista, para luego realizar la operación desde una de las funciones de Pandas-Python
# Matriz de Correlación
mediciones = tablaEM[sensor_EM].copy()
correlacion_matriz = mediciones.corr()
obteniendo como resultados:
Matriz de correlación:
TEMP Humidity Solar_rad Bar_press.
TEMP 1.000000 -0.957730 0.743379 -0.387187
Humidity -0.957730 1.000000 -0.765766 0.447845
Solar_rad 0.743379 -0.765766 1.000000 -0.093236
Bar_press. -0.387187 0.447845 -0.093236 1.000000
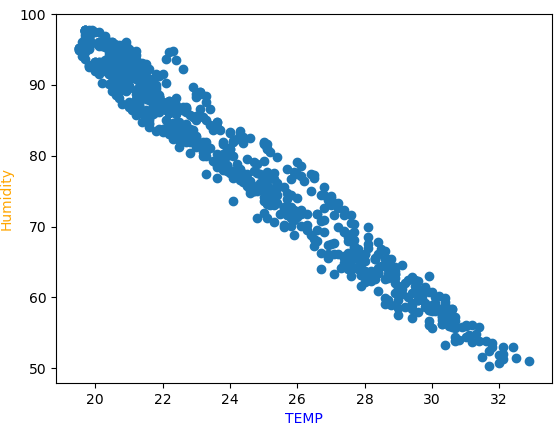
Del resultado se observa que el coeficiente de correlación entre las mediciones de «TEMP» y «Humidity» es alta. Para observar el caso se usa la gráfica entre las dos variables comparando los datos en el tiempo por fechas.
Cuando la temperatura aumenta la Humedad disminuye, lo opuesto tambien es observable.
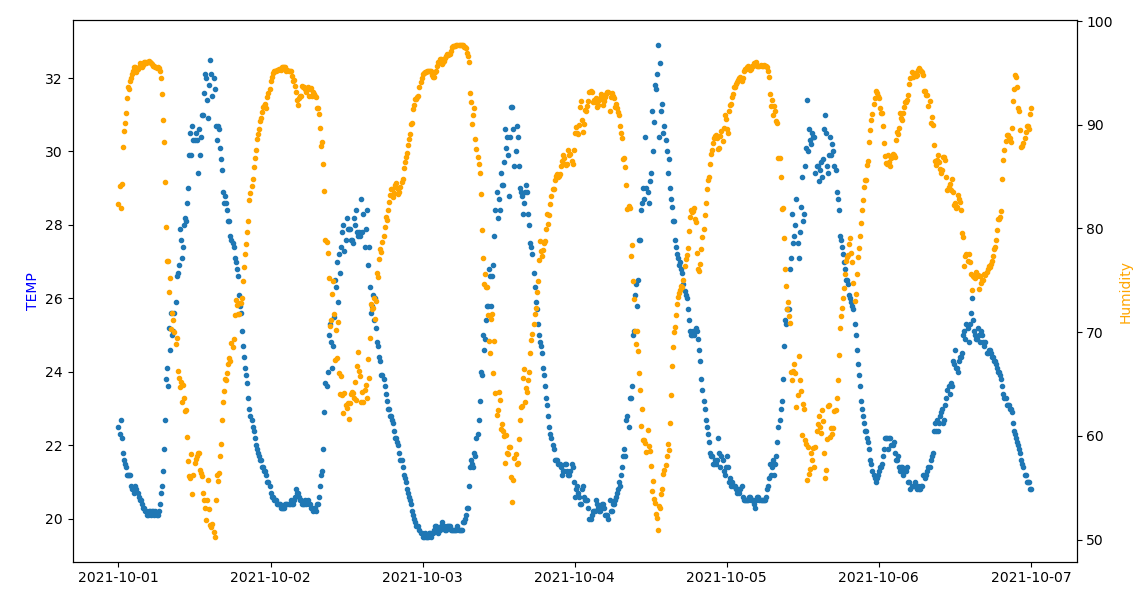
Comparando solo entre las dos variables:
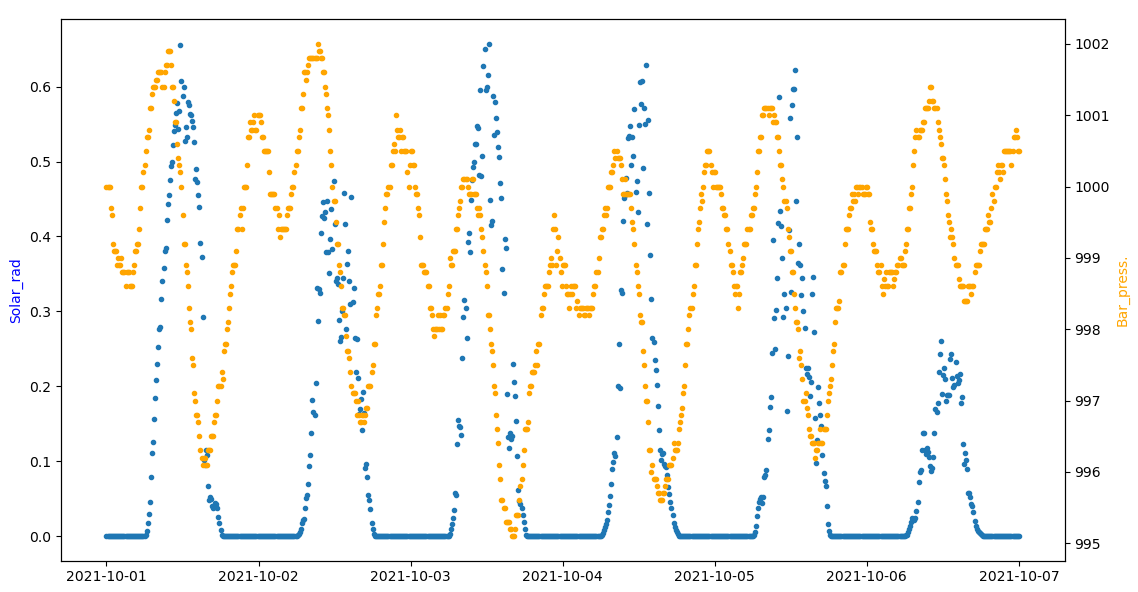
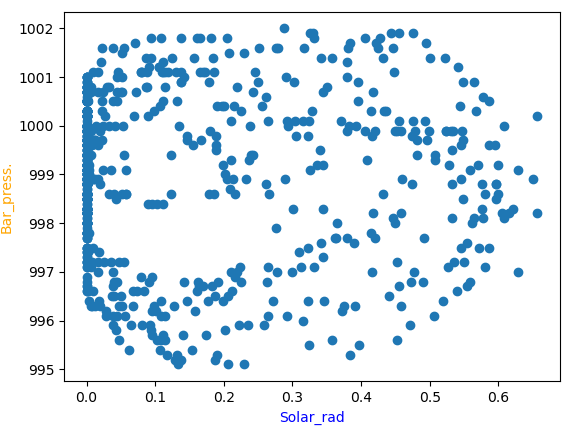
Para el caso de radiación solar y presión baromérica, el coeficiente de correlación es «bajo».
comparando entre las dos variables solamente:
Instrucciones en Python
# Archivos de estación meteorologica # correlacion entre sensor_EM import numpy as np import pandas as pd import datetime as dt import os import matplotlib.pyplot as plt from matplotlib.dates import DateFormatter, DayLocator # INGRESO archivoEM = "2021_10_EstMeteorologica.csv" sensor_EM = ["TEMP","Humidity","Solar_rad","Bar_press."] sensor_EM_u = ["(°C)","(%)","(kW)","(hPa)"] # PROCEDIMIENTO # tabla estacion meteorologica tablaEM = pd.read_csv(archivoEM, sep=';',decimal=',') tablaEM = pd.DataFrame(tablaEM) tablaEM_n = len(tablaEM) # Matriz de Correlación mediciones = tablaEM[sensor_EM].copy() correlacion_matriz = mediciones.corr() # SALIDA print('Matriz de correlación:') print(correlacion_matriz)
Para añadir las gráficas, se añaden instrucciones para seleccionar las variables en intervalos de fechas.
# tabla estacion meteorologica fechaformatoEM = "%d/%m/%Y %H:%M:%S" # fechas concatenando columnas de texto tablaEM['fecha'] = tablaEM['Date']+' '+tablaEM['Time'] tablaEM['fecha'] = pd.to_datetime(tablaEM['fecha'], format=fechaformatoEM) # grafica sensorA = "TEMP" sensorB = "Humidity" fechaA = "2021/10/01" fechaB = "2021/10/07" ti = tablaEM["fecha"].loc[tablaEM["fecha"].between(fechaA,fechaB)] xi = tablaEM[sensorA].loc[tablaEM["fecha"].between(fechaA,fechaB)] yi = tablaEM[sensorB].loc[tablaEM["fecha"].between(fechaA,fechaB)] # grafica compara sensores en tiempo fig_Pt, graf1 = plt.subplots() graf1.scatter(ti,xi, marker = '.', label=sensorA) eje12 = graf1.twinx() # segundo eje del grafico eje12.scatter(ti,yi, marker = '.', color='orange',label=sensorB) graf1.set_ylabel(sensorA, color='blue') eje12.set_ylabel(sensorB, color='orange') plt.show() # grafica compara sensores plt.scatter(xi,yi) plt.xlabel(sensorA, color='blue') plt.ylabel(sensorB, color='orange') plt.show()