Referencia: Ejemplo León-García 4.36 p180
Sea Y=cos(X), y supondremos que X es uniformemente distribuida en el intervalo de (0, 2π]. Y puede ser vista como una muestra de una señal sinusoidal a un instante aleatorio de tiempo que esta uniformemente distribuida en el periodo de la sinusoide.
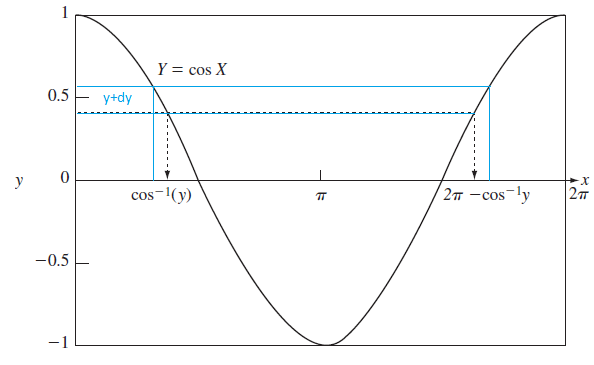
Para encontrar la pdf, se tiene que la variable -1< y < 1
f_Y(y)=\left.\sum_{k} \frac{f_X(x)}{|dy/dx|} \right|_{x=x_k}
La función fX(x) es uniforme, por lo que el área del integral en el intervalo debe ser 1, es decir:
\int_{0}^{2\pi}c dx=1
=(2\pi-0)*c= 2\pi c = 1
c=\frac{1}{2\pi}
f_X(x) = \frac{1}{2\pi}
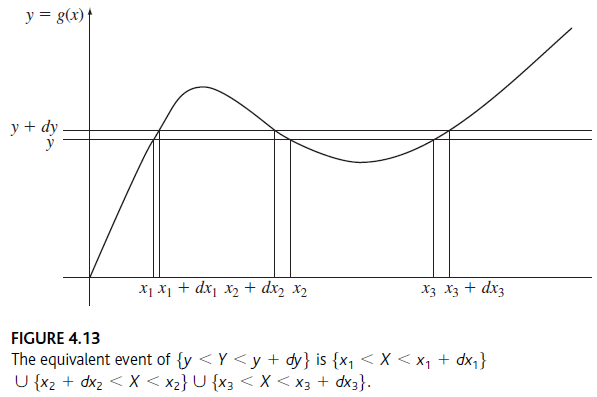
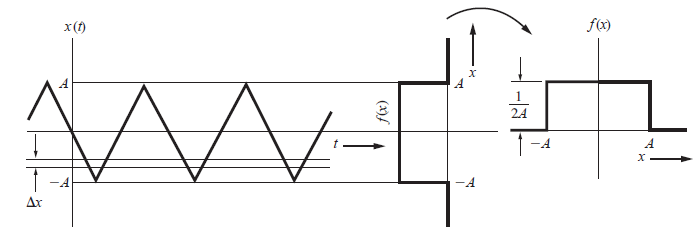
De la figura se encuentra que la ecuación tiene dos puntos de intersección o dos soluciones:
x_0 = \cos ^{-1}(y)
x_1 = 2\pi- x_0
por lo que se evalúa la derivada en cada punto de intersección:
\left.\frac{dy}{dx} \right|_{x_0}= -sin(x_0) = - sin(cos^{-1}(y))
\alpha = \cos^{-1}(x)
\sin(\alpha) = y
x^2 + y^2 =1
x = \sqrt{1-y^2}
\left.\frac{dy}{dx} \right|_{x_0}= -\sqrt{1-y^2}
\left.\frac{dy}{dx} \right|_{x_1}= -\sqrt{1-y^2}
dado que y0 = y1 = y
Aplicando la ecuación primera:
f_Y(y) = \frac{1}{2\pi \sqrt{1-y^2}} + \frac{1}{2\pi \sqrt{1-y^2}}
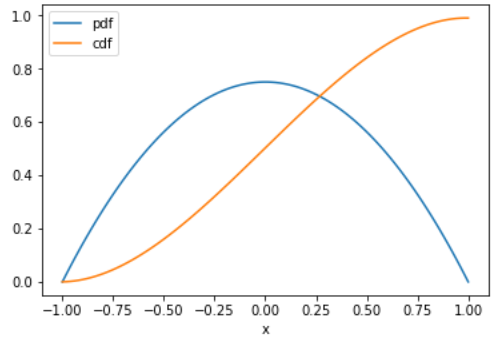
= \frac{1}{\pi \sqrt{1-y^2}}
-1 < y < 1
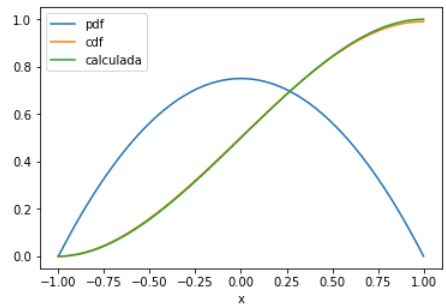
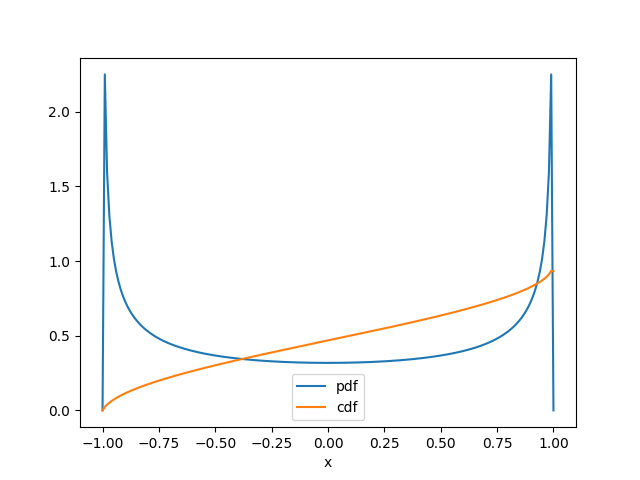
Gráfica del resultado
# pdf de una señal senoidal
import matplotlib.pyplot as plt
import numpy as np
# INGRESO
# n=int(input('numero de muestras: '))
n = 200
# PROCEDIMIENTO
t = np.linspace(-1,1,n)
fy = np.zeros(n,dtype=float)
# Evaluar denominador no cero
for i in range(0,n,1):
denominador = 1-t[i]**2
if (denominador!=0):
fy[i] = 1/(np.pi*np.sqrt(1-t[i]**2))
dt = t[1]-t[0]
Fy = np.cumsum(fy)*dt
# SALIDA
plt.plot(t,fy,label='pdf')
plt.plot(t,Fy,label='cdf')
plt.xlabel('x')
plt.legend()
plt.show()
Cálculo con un método numérico
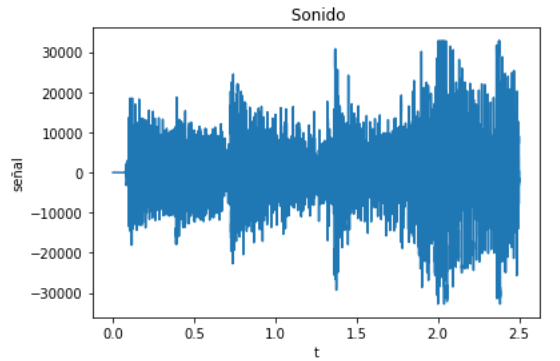
Señal Coseno(x), pmf, cdf
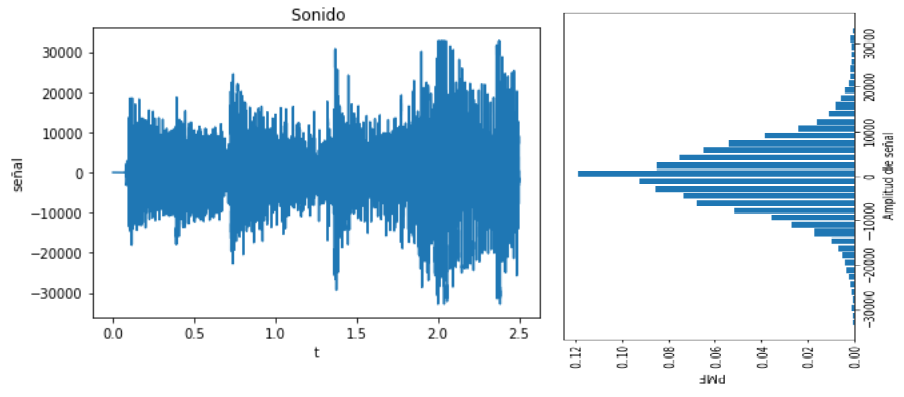
Se obtiene barriendo una ventana horizontal estrecha de Δx voltios de ancho, verticalmente a lo largo de las formas de onda y después midiendo la frecuencia relativa de la ocurrencia de voltajes en la ventana Δx.
El eje de tiempo se divide en n intervalos y la forma de onda aparece nΔx veces dentro de estos intervalos en la ventana Δx.
Para observar lo indicado usando python, se presenta el siguiente grupo de instrucciones:
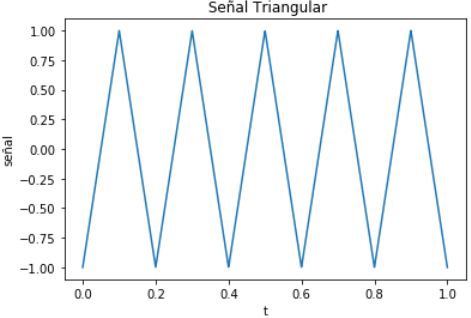
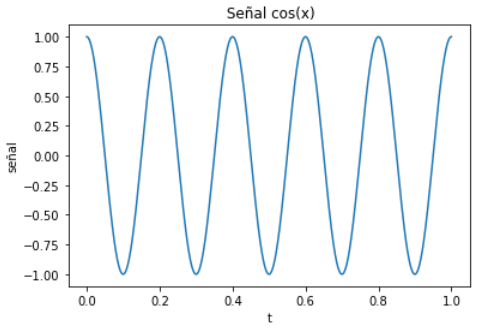
Genera la señal
En un intervalo [a,b] de tiempo, con n muestras en el intervalo y una señal coseno(x) con frecuencia fs Hz.
# Pmf de una senal periódica conocida
# definir la señal en la sección senal_t
import numpy as np
import scipy.signal as signal
import scipy.stats as stats
import matplotlib.pyplot as plt
def senal_t(t, fs):
m = len(t)
y = np.zeros(m, dtype=float)
for i in range(0,m,1):
y[i] = np.cos(2 * np.pi * fs * t[i])
return(y)
# INGRESO
# Frecuencia de la señal en Hz
fs = 5
# Rango en tiempo de la señal y muestras
a = 0
b = 1
tramos = 2000
# PROCEDIMIENTO
muestreo = tramos+1
t = np.linspace(a, b, muestreo)
senal = senal_t(t, fs)
# SALIDA
plt.plot(t,senal)
plt.title(' Señal sen(x)')
plt.xlabel('t')
plt.ylabel('señal')
plt.show()
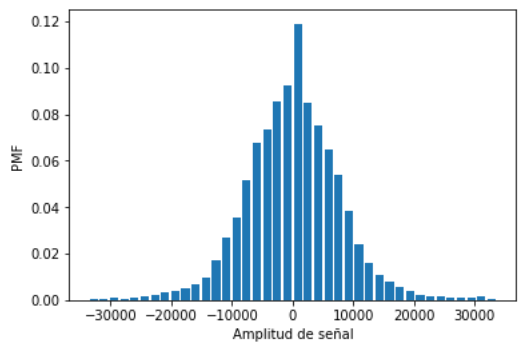
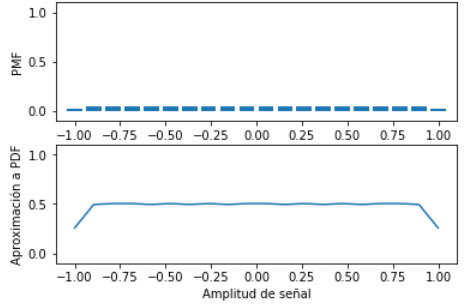
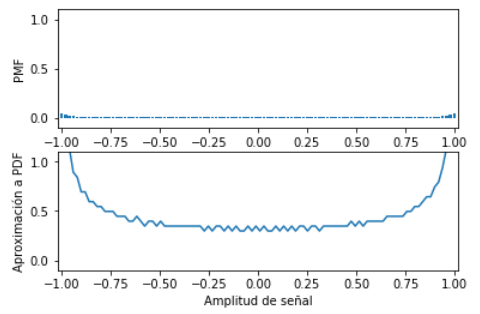
Determinar la función de probabilidad de masa PMF
Se divide el rango de valores posibles de la señal en m intervalos.
Para simplificar el conteo de valores por rango se usa la función scypy.stats.relfreq, que cuenta en m intervalos entre el rango de la señal, dando como resultado las frecuencias relativas a intervalos Δx.
\sum_{i=0}^{N} p_i(x)=1
Si se considera aproximar la función a contínua para observación, será necesario compensar el vector de relativas al dividir por Δx pues el conteo relativo depende del número de divisiones m.
# Pmf de una senal periódica conocida
# definir la señal en la sección senal_t
import numpy as np
import scipy.signal as signal
import scipy.stats as stats
import matplotlib.pyplot as plt
def senal_t(t, fs):
m = len(t)
y = np.zeros(m, dtype=float)
for i in range(0,m,1):
y[i] = np.cos(2 * np.pi * fs * t[i])
return(y)
# INGRESO
# Frecuencia de la señal en Hz
fs = 5
# Rango en tiempo de la señal y muestras
a = 0
b = 1
tramos = 2000
# PROCEDIMIENTO
muestreo = tramos+1
t = np.linspace(a, b, muestreo)
senal = senal_t(t, fs)
# SALIDA
plt.plot(t,senal)
plt.title(' Señal sen(x)')
plt.xlabel('t')
plt.ylabel('señal')
plt.show()
# Función de Probabilidad de Masa, PMF
m = 50 # intervalos en análisis
#PROCEDIMIENTO
relativa = stats.relfreq(senal, numbins = m )
deltax = relativa.binsize
# considerando el deltax, para valor de PMF
relcontinua=relativa.frequency/deltax
# Eje de frecuencias, por cada deltax
senalmin = np.min(senal)
senalmax = np.max(senal)
senalrango = np.linspace(senalmin,senalmax,m)
# SALIDA
print('frecuencia relativa:')
print(relativa.frequency)
print('Rango de Señal')
print(senalrango)
print('Aproximación a contínua')
print(relcontinua)
# SALIDA Grafico de PMF
plt.subplot(211)
plt.bar(senalrango,relativa.frequency, width=deltax*0.8)
plt.xlabel('Amplitud de señal')
plt.ylabel('PMF')
plt.subplot(212)
plt.plot(senalrango,relcontinua)
plt.ylim(ymin=0,ymax=np.max(relcontinua))
plt.xlabel('Amplitud de señal')
plt.ylabel('Aproximación a PDF')
plt.show()
frecuencia relativa:
[ 0.045 0.034 0.023 0.018 0.017 0.014 0.014 0.012 0.012 0.011 0.011 0.01 0.01 0.01 0.009 0.009 0.009 0.008 0.008 0.009 0.008 0.007 0.008 0.008 0.007 0.008 0.007 0.007 0.007 0.007
...
0.008 0.007 0.008 0.008 0.008 0.008 0.008 0.009 0.009 0.009 0.009 0.009 0.01 0.01 0.011 0.011 0.012 0.013 0.013 0.015 0.016 0.019 0.023 0.033 0.046]
Rango de Señal
[-0.99999877 -0.97979676 -0.95959475 -0.93939274 -0.91919073 -0.89898873 -0.87878672 -0.85858471 -0.8383827 -0.8181807 -0.79797869 -0.77777668 -0.75757467 -0.73737266 -0.71717066 -0.69696865 -0.67676664 -0.65656463
...
0.63636386 0.65656587 0.67676788 0.69696988 0.71717189 0.7373739 0.75757591 0.77777791 0.79797992 0.81818193 0.83838394 0.85858595 0.87878795 0.89898996 0.91919197 0.93939398 0.95959598 0.97979799 1. ]
Aproximación a contínua
[ 2.22750138 1.68300104 1.1385007 0.89100055 0.84150052 0.69300043 0.69300043 0.59400037 0.59400037 0.54450034 0.54450034 0.49500031 0.49500031 0.49500031 0.44550028 0.44550028 0.44550028 0.39600024
...
0.39600024 0.44550028 0.44550028 0.44550028 0.44550028 0.44550028 0.49500031 0.49500031 0.54450034 0.54450034 0.59400037 0.6435004 0.6435004 0.74250046 0.79200049 0.94050058 1.1385007 1.63350101 2.27700141]
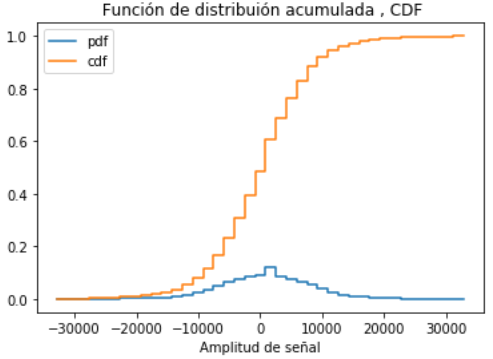
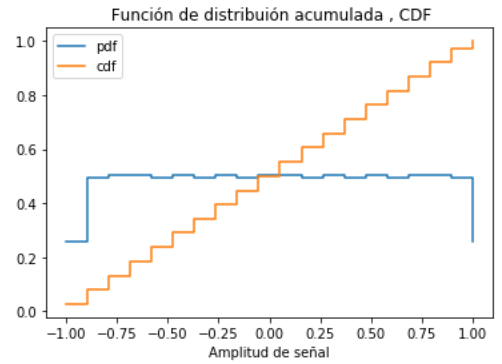
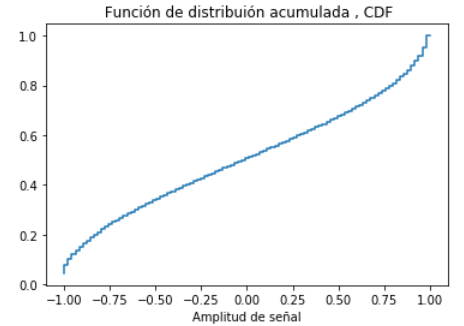
Determinar la Función de distribucíón acumulada
Considere el caso discreto, solo es necesario ir acumulando los valores de «relativa».
Al usar la aproximación a contínua, la sumatoria debe considerar el área bajo la curva, por lo que los valores se multiplican por Δx antes de acumular los valores de las frecuencias.
# Función distribución acumulada
acumulada=np.cumsum(relcontinua*deltax)
# Salida CDF
# plt.step(senalrango,relcontinua,label='pdf', where='post')
plt.step(senalrango,acumulada,label='cdf', where='post')
plt.xlabel('Amplitud de señal')
plt.title(' Función de distribuión acumulada , CDF')
plt.legend()
plt.show()
Tarea: realice el ejercicio con otras señales periódicas.
Referencia: Leon W Couch apéndice B p675