Publicado en

Densidad Espectral de Potencia Concepto

Referencia: León García 10.1.1 p578

Sea X(t) un proceso aleatorio contínuo en el tiempo estacionario en el sentido amplio WSS, con media mX y función de autocorrelación RX(t).

Si cambiamos el dominio de la función desde tiempo a frecuencia, lo anterior deberá también cambiarse de dominio. Si la función densidad de probabiliad se cambia de dominio, se conocería como periodograma estimador, y se llega a determinar la densidad espectral de potencia de X(t) definida como:

S_X (f) = lim_{T \rightarrow \infty} \frac{1}{T} E \left[ \left| \tilde{x} (f) \right| ^2\right]

La densidad espectral de potencia de X(t) está dada por la transformada de Fourier de la función de autocorrelación:

S_X (f) = Fourier\{R_x(\tau) \} = \int_{-\infty}^{\infty} R_x(\tau) e^{-j2\pi f \tau} d\tau

La potencia promedio de X(t) se expresa también como:

E[ X^2(t)] = R_X(0) = \int_{-\infty}^{\infty} S_X (f) df

La densiddad espectral de potencia también se relaciona con la autocorrelación y autocovarianza por medio de la transformada de Fourier:

S_X(f) = Fourier\{ C_x (\tau) + m^2_x\}

si consideramos que m_x es un componente constante o «DC»

S_X(f) = Fourier\{ C_x (\tau)\} + m^2_x \delta(f)

ampliando el concepto a densidad espectral de potencia cruzada SX,Y (f) se define como:

S_{X,Y}(f) = Fourier\{ R_{X,Y} (\tau) \}
Publicado en

Autocorrelación Propiedades

Referencia León-García 9.6 p522

Potencia Promedio

La función autocorrelación a τ=0 entrega la potencia promedio (segundo momento) del proceso:

R_{X}(0) = E[X(t)^2]

para todo valor de t

Función par respecto a τ

R_{X}(\tau) = E[X(t+\tau)X(t)] = E[X(t)X(t+\tau)] = R_{X}(-\tau)

Mide la tasa de cambio

La función de autocorrelación es una medida de la tasa de cambio de un proceso aleatorio

P[|X(t+\tau) - X(t)| > \epsilon] = P[(X(t+\tau) - X(t))^2 > \epsilon ^2] \leq \frac{E[(X(t+\tau) - X(t))^2]}{\epsilon ^2} =\frac{2\{R_X(0) - R_X(\tau) \}}{\epsilon ^2}

como resultado de usar la inequidad de Markov

tiene maximo en τ=0

si se usa la inequidad de Cauchy-Schwarz:

E[XY]^2 \leq E[X^2]E[Y^2] R_X(\tau )^2 = E[X(t+ \tau) X(t)]^2 \leq E[X^2(t+ \tau)] E[X^2(t)] = R_X(0) |R_X(\tau)| \leq R_X(0)

Periódica en media cuadrática

si R_X(0) = R_X(d) , entonces R_X(\tau) es periódica con periodo d y X(t) es «periódica en media cuadrática».

R_X(\tau + d)| = R_X(\tau)

se aproxima a el cuadrado de la media cuando τ tiende a infinito

Publicado en

Proceso aleatorio estacionario

Referencia: León-García 9.6, 9.6.1 p518,521; Gubner 10.3, 10.2 p395, p392; Ross 10.7 p654, p656

Estacionario

Un proceso aleatorio discreto o contínuo en el tiempo 
X(t) es estacionario si la distribución conjunta de 
cualquier grupo de muestras No depende de la ubicación 
del tiempo de origen.
F_{X(t_1),..., X(t_k)} (x_1, ... x_k) = F_{X(t_1+\tau),..., X(t_k)} (x_1, ... x_k+\tau)

para cualquier τ, k, o muestras t1, … , tk.

Estacionario con cdf de 1er Orden

Un proceso aleatorio estacionario con cdf de primer orden debe ser independiente del tiempo

F_{X(t)} (x) = F_{X(t+\tau)} (x) = F_X(x)

para todo t, τ, dicho de otra forma, sus resultados son constantes

m_{X}(t) = E[X(t)]=m VAR[X(t)] = E[(X(t)-m)^2] = \sigma ^2

Estacionario con cdf de 2do Orden

Un proceso aleatorio estacionario con cdf de segundo orden debe depender solo de la diferencia de tiempo entre muestras y NO en particular del tiempo de las muestras

F_{X(t_1),X(t_2)} (x_1,x_2) = F_{X(0),X(t_2-t_1)} (x_1,x_2)

para todo t1, t2

R_{X}(t_1,t_2) = R_{X} (t_2-t_1) C_{X}(t_1,t_2) = C_{X} (t_2-t_1)

Estacionario en el Sentido Amplio (WSS o débil)

 Un proceso aleatorio discreto o contínuo en el tiempo 
X(t) es estacionario en el sentido amplio (WSS) 
si satiface que:
m_X(t) = m C_{X}(t_1,t_2) = C_{X} (t_2-t_1)

De forma semejante, los procesos X(t) y Y(t) son estacionarios conjuntos si ambos son estacionarios en el sentido amplio y si covarianza cruzada depende solo de t1-t2.

R_{X}(t_1,t_2) = R_{X} (\tau) C_{X}(t_1,t_2) = C_{X} (\tau)
Publicado en

Autocovarianza PM

Referencia: León García Ejemplo 9.10 p495, Gubner Ejemplo 10.8 p389, Gubner Ejemplo 10.17 p396

Sea X(t) = cos(ω t + Φ), donde Φ es uniforme en el intervalo (-π,π) Encontrar la autocovarianza de X(t).

la variable aleatoria Φ tiene distribución uniforme en el intervalo, por lo que la función fΦ(φ) es constante = 1/[π – (-π)] = 1/2π.

Recordamos que:

E[g(x)] = \int_{-\infty}^{\infty} g(x) f(x) dx

Media (León-García 4.15 p158):

m_X(t) = E[cos(\omega t + \Phi)] = = \int_{-\pi}^{\pi} cos(\omega t + \Phi) \frac{1}{2\pi} d\Phi = \left. \frac{-1}{2\pi} (sin (\omega t + \Phi)) \right|_{-\pi}^{\pi} = \frac{-1}{2\pi} [sin (\omega t + (-\pi)) - sin (\omega t + \pi)] = 0

Autocovarianza

dado que el valor esperado es cero, la autocovarianza es igual a la autocorrelación

C_{X} (t_1,t_2) = R_X (t_1,t_2) - E[X(t_1,t_2)] = R_X (t_1,t_2) = E[cos(\omega t_1 + \Phi) cos(\omega t_2 +\Phi)]

Recordando que:

E[g(x)] = \int_{-\infty}^{\infty} g(x) f(x) dx cos(x) cos(y) = \frac{cos(x-y) + cos(x+y) }{2}

se tiene que:

= \int_{-\pi}^{\pi} [cos(\omega t_1 + \Phi) cos(\omega t_2 +\Phi)] \frac{1}{2\pi} d\Phi = \int_{-\pi}^{\pi} \frac{cos(\omega (t_1 - t_2))+cos(\omega (t_1 + t_2)+ 2\Phi)}{2} \frac{1}{2\pi} d\Phi = \int_{-\pi}^{\pi} \frac{cos(\omega (t_1 - t_2))}{2} \frac{1}{2\pi} d\Phi + \int_{-\pi}^{\pi} \frac{cos(\omega (t_1 + t_2 )+ 2\Phi)}{2} \frac{1}{2\pi} d\Phi

El primer integral, el coseno no depende de Φ, mientras que el segundo integral es semejante al intergral de la media y cuyo resultado es cero.

= \left. \frac{cos(\omega (t_1 - t_2))}{2} \frac{\Phi}{2\pi} \right|_{-\pi}^{\pi} + 0
C_{X} (t_1,t_2) = R_X (t_1,t_2) =
= \frac{1}{2} cos(\omega (t_1 - t_2))

Publicado en

Autocovarianza en AM

Referencia: León García Ejemplo 9.9 p495, Gubner Ej10.35 p496

Sea X(t) = A cos(2πt), donde A es una variable aleatoria, con un comportamiento semejante a la figura.

Encontrar el valor esperado , la autocorrelación y autocovarianza de de X(t).

El valor esperado se calcula a continuación, note que la media varia respecto a t y que el valor es cero para valores de t donde cos(2πt) =0.

E[X(t)] = E[A cos(2\pi t)] E[X(t)] = E[A] cos(2\pi t)

La autocorrelación es:

R_X(t_1,t_2) = E[A cos(2\pi t_1) A cos(2\pi t_2)] = E[A^{2} cos(2\pi t_1) cos(2\pi t_2)] = E[A^{2}] cos(2\pi t_1) cos(2\pi t_2)

usando:

2 cos(x)cos(y) = cos(x-y) + cos(x+y) cos(x)cos(y) = \frac{ cos(x-y) + cos(x + y)}{2}

se reemplaza:

= E[A^{2}] \frac{1}{2}[cos(2\pi t_1 - 2\pi t_2) + cos(2\pi t_1 + 2\pi t_2)] R_X(t_1,t_2) = E[A^{2}] \frac{[cos(2\pi (t_1 - t_2)) + cos(2\pi (t_1 + t_2))]}{2}

se observa que el valor de autocorrelación depende de las diferencias de tiempo t1 y t2.

La autocovarianza es:

Cov_X(t_1,t_2) = R_X(t_1,t_2) - E[X(t_1)]E[X(t_2)] = E[A^{2}] cos(2\pi t_1) cos(2\pi t_2) - E[A] cos(2\pi t_1)E[A] cos(2\pi t_2) = E[A^{2}] cos(2\pi t_1) cos(2\pi t_2) - E[A]^2 cos(2\pi t_1)cos(2\pi t_2) = (E[A^{2}] - E[A]^2) cos(2\pi t_1)cos(2\pi t_2) = Var[A] cos(2\pi t_1)cos(2\pi t_2)

con el mismo procedimiento de cos(x)cos(y):

Cov_X(t_1,t_2) = Var[A] \frac{[cos(2\pi (t_1 - t_2)) + cos(2\pi (t_1 + t_2))]}{2}
Publicado en

Autocorrelación, Autocovarianza con variable tiempo

Referencia: León-García 9.2.2 p493

Se puede usar los momentos de muestras en el tiempo para parcialmente especificar un proceso aleatorio al resumir la información contenida en las cdf conjuntas.

Procesos aleatorios Contínuos en tiempo

Media:

m_X(t) = E[X(t)] = \int_{-\infty}^{\infty} x f_{X(t)}(x) dx

Varianza:

VAR[X(t)] = \int_{-\infty}^{\infty} ( x - m_X(t))^2 f_{X(t)}(x) dx

donde f_{X(t)}(x) es la pdf de X(t). Note que ambas son funciones determinísticas de tiempo.

Autocorrelación

R_X(t_1,t_2) = E[X(t_1,t_2)] = = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} xy f_{X(t_1),X(t_2)}(x,y) dx dy

Autocovarianza:

C_X(t_1,t_2) = E[\{X(t_1) - m_X(t_1) \} \{ X(t_2) - m_X(t_2)\} C_X(t_1,t_2) = R_X(t_1,t_2) - m_X(t_1) m_X(t_2)

coeficiente de correlación

\rho (t_1, t_2) = \frac{C_x(t_1,t_2)}{\sqrt{C_x(t_1,t_1)}\sqrt{C_x(t_2,t_2)}}

El coeficiente de correlación es la medida en la cual una variable aleatoria puede predecirse como una función lineal de otra.

Procesos aleatorios Discretos en tiempo

Media:

m_X(n) = E[X(n)]

Varianza:

VAR[X(n)] = E[(X(n) - m_X(n))^2]

Autocorrelación

R_X(n_1,n_2) = E[X(n_1,n_2)]

Autocovarianza:

C_X(n_1,n_2) = E[\{X(n_1) - m_X(n_1) \} \{ X(n_2) - m_X(n_2)\} C_X(n_1,n_2) = R_X(n_1,n_2) - m_X(n_1) m_X(n_2)

 

Publicado en

Funciones de una Variable aleatoria

Sea X una variable aleatoria y sea g(x) una función de valor real definida en el eje real.

Defina Y= g(X), esto es. Y está determinada por la evaluación de la función en g(x) en el valor que ha tomado la variable aleatoria X.  Entonces Y también es una variable aleatoria.

Las probabilidades de los valores para Y dependen de la función g(x) así como la función distribución acumulada de X.

Considere una función no lineal Y=g(X) como la que se muestra en la figura.

donde |dy| es la longitud del intervalo y < Y ≤ (y+dy).
De forma similar, la probabilidad que el evento en cada intervalo es aproximadamente

f_Y(y)=\left.\sum_{k} \frac{f_X(x)}{|dy/dx|} \right|_{x=x_k} =\left.\sum_{k} f_X(x) \left| \frac{dx}{dy} \right| \right|_{x=x_k}

Ejemplo: León García 4.30 p.176

Sea X el valor de las muestras de voltaje de una señal de voz, y suponga que X tiene una distribución uniforme en el intervalo [-4d,4d].

Sea Y = q(X), donde la función característica de entrada-salida de un cuantizador (convertidor analógico-digital) se muetra en la figura. Encuentre la función de probabilidad de masa para Y.

Solución: El evento {Y=q} para q en SY es equivalente al evento {X en Iq}, donde Iq es un intervalo de puntos equivalentes mapeados en representación al punto q. La pmf de Y se encuentra evaluando:
P[Y=q] = \int_{I_q} f_X(t) dt

Lo que permite ver fácilmente que la representación de un punto tiene un intervalo de longitud d mappeado en él. Entonces existirán ocho posibles salidas equiprobables, es decir, P[Y=q] = 1/8 para q en SY–

Publicado en

Metodo de la Transformada

Referencia: Gubner 4.3 p159, León García 7.6.2 p 398

Los metodos de transformadas son muy útiles para cálculos que involucran derivadas e integrales de funciones. Muchos problemas involucran el uso de la «convolución» de dos funciones f1(x) * f2(x), cuyo cálculo se facilita si se tabaja con un método de transformadas.

Usar por ejemplo la transformada de Fourier, al cambiar de dominio convierte la convolución de funciones en una multiplicación, al resultado se le realiza la antitransformada y se obtiene el resultado buscado.

Función característica

Sea X una variable aleatoria contínua con función densidad de probabilidad f(x), entonces:

\Phi_{X} (\omega) = E\left[ e^{j \omega X} \right] = \int_{-\infty}^{\infty} f_{X}(x) e^{j\omega x} dx \text{donde } j=\sqrt{-1}

lo que también es la transformada de Fourier de f, la fórmula para invertir la transformada es:

f_{X}(x) = \frac{1}{2\pi} \int_{-\infty}^{\infty} \Phi_{X}(\omega) e^{-j\omega x} d\omega

Es una transformación de la función desde el dominio del tiempo (t) al dominio de la frecuencia (ω).

Nota: En los libros de sistemas y señales, se define la transformada de Fourier de f por \int_{-\infty}^{\infty} e^{-j\omega x} dx . Para ser mas preciso, se debería decir φX(v) es la transformada de Fourier evaluada en -v.

Convolutions | Why X+Y in probability is a beautiful mess. 3Blue1Brown. 27 junio 2023.

Publicado en

cdf – Modulación AM

Referencia: Leon W Couch 4-2 p234, «El Aguacate» introducción

Modulación en Amplitud (AM)

La modulación es el proceso de codificación de la información fuente, sonido o moduladora, dentro de una señal pasabanda s(t), resultande o modulada. La señal modulada se obtiene de:

senal(t) = A_c[1+moduladora(t)] cos(\omega_c t) s(t) = A_c[1+m(t)] cos(\omega_c t)

donde:

\omega_c = 2\pi f_c

fc es la frecuencia de la portadora o «carrier».
Ac es la amplitud de la portadora.

Como ejemplo, si se quiere enviar una señal de sonido obtenida de un archivo.wav modulada en Amplitud, la señal m(t) será:

muestra_GuitarraCuerda.wav

Instrucciones en Python

# pmf de un sonido
# entrada es archivo01
# propuesta:edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import scipy.io.wavfile as waves
import scipy.stats as stats

# INGRESO 
# archivo01 = input('archivo de sonido 01: ' )
# k = int(input('muestras para ejemplo: '))
archivo01 = 'muestra_GuitarraCuerda.wav'
k = 500

# PROCEDIMIENTO
muestreo, sonido01 = waves.read(archivo01)

# Extrae un canal en caso de estéreo
canales = sonido01.shape
cuantos = len(canales)
canal = 0   
if (cuantos==1): # Monofónico
    uncanal = sonido01[:]  
if (cuantos>=2): # Estéreo
    uncanal = sonido01[:,canal]
    
moduladora = uncanal[0:k].astype(float)
dt = 1/muestreo
t  = np.arange(0,k*dt,dt)

# SALIDA GRAFICA
plt.plot(t,moduladora)
plt.title(' Moduladora m(t)')
plt.xlabel('t')
plt.ylabel('señal')
plt.plot()
plt.show()

Para el ejemplo, la señal de la portadora presentada tiene frecuencia de 5500 para que se pueda visualizar el efecto.
(Revisar frecuencias de portadoras AM estándares o ver el dial de un radio AM).

# Portadora:
fc = 5500
portadora = np.cos(2*np.pi*fc*t)

# SALIDA GRAFICA
plt.plot(t,portadora, color='orange')
plt.title(' Portadora')
plt.xlabel('t')
plt.ylabel('señal')
plt.plot()
plt.show()

Antes de aplicar la moduladora, se la normaliza para mantener la proporción en la gráfica

# normalizar y subir a positiva
moduladoranorm = moduladora/np.max(moduladora)
moduladora = (1+ moduladoranorm)

# Modular portadora
Ac = 1
modulada = Ac*moduladora*portadora

# SALIDA GRAFICA
plt.plot(t,moduladora,label='moduladora')
plt.plot(t,modulada,label='modulada')
plt.title(' Señal modulada S(t)')
plt.xlabel('t')
plt.ylabel('señal')
plt.legend()
plt.show()

Publicado en

cdf – una señal de sonido

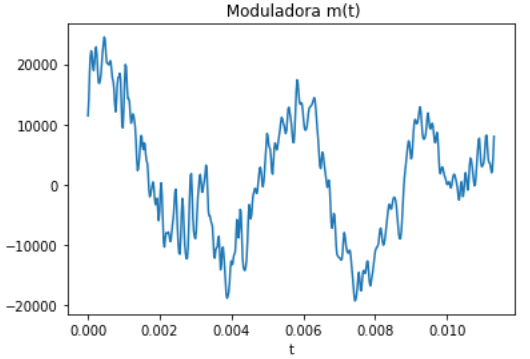
Referencia: Leon W Couch apéndice B p675, «El Aguacate», pasillo introducción, Archivos de Audio.wav – Abrir, extraer una porción

De forma semejante al análisis para una señal triangular, se obtiene barriendo una ventana estrecha de Δx voltios de ancho, verticalmente a lo largo de las formas de onda y después midiendo la frecuencia relativa de la ocurrencia de voltajes en la ventana Δx.

El eje de tiempo se divide en n intervalos y la forma de onda aparece nΔx veces dentro de estos intervalos en la ventana Δx.

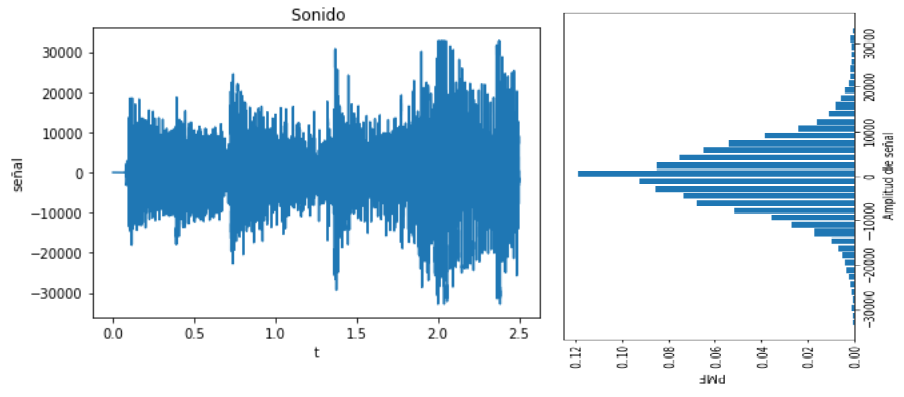
Se inicia abriendo el archivo 'muestra01_ElAguacateIntro.wav', seleccionando un canal en caso de ser estéreo. Para los cálculos se convierte a números reales ‘float’ de tipo estándar de python y para la gráfica se determina el rango de tiempo 't'.

# pmf de un sonido
# entrada es arcchivo01
# propuesta:edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import scipy.io.wavfile as waves
import scipy.stats as stats

# INGRESO 
# archivo01 = input('archivo de sonido 01:' )
archivo01 = 'muestra01_ElAguacateIntro.wav'

# PROCEDIMIENTO
muestreo, sonido01 = waves.read(archivo01)

# Extrae un canal en caso de estéreo
canales=np.shape(sonido01)
cuantos=len(canales)
canal = 0   
if (cuantos==1): # Monofónico
    uncanal=sonido01[:]  
if (cuantos>=2): # Estéreo
    uncanal=sonido01[:,canal]
    
senal=uncanal.astype(float)
dt=1/muestreo
n=len(senal)
t=np.arange(0,n*dt,dt)

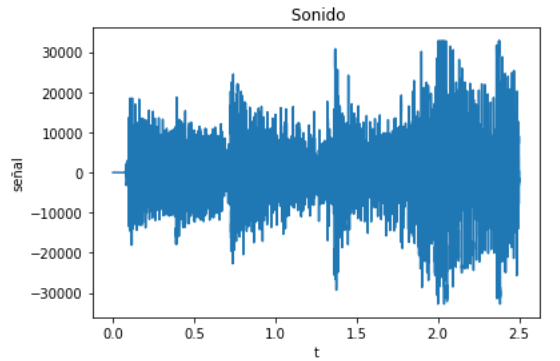
Se grafica la señal en observación de uncanal:

# SALIDA GRAFICA
plt.plot(t,senal)
plt.title(' Sonido')
plt.xlabel('t')
plt.ylabel('señal')
plt.plot()
plt.show()


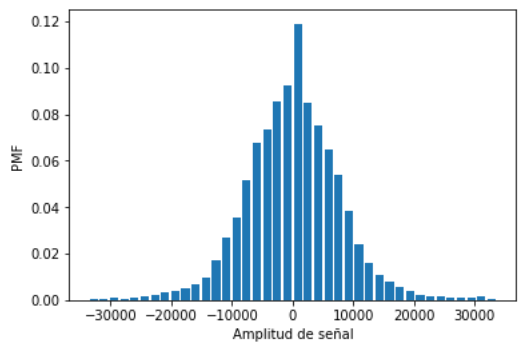
Aplicando luego el mismo algoritmo usado para señales triangulares y senoidales, manteniendo la forma discreta.

# Función de Probabilidad de Masa, PMF
m=40  # intervalos eje vertical

#PROCEDIMIENTO
relativa = stats.relfreq(senal, numbins = m )
deltax=relativa.binsize

# Eje de frecuencias, por cada deltax
senalmin=np.min(senal)
senalmax=np.max(senal)
senalrango=np.linspace(senalmin,senalmax,m)

# SALIDA
print('frecuencia relativa:')
print(relativa.frequency)
print('Rango de Señal')
print(senalrango)

frecuencia relativa:
[ 0.00023583  0.00073469  0.00089796  0.00053515  0.00084354  0.00179592  0.00245805  0.00306576  0.0039093   0.00504308  0.0066576   0.0099229  0.01693424  0.02671202  0.03568254  0.05160998  0.06758277  0.07323356  0.08575057  0.09217234  0.11898413  0.08494331  0.07535601  0.06454422  0.05382313  0.03821315  0.02429932  0.01573696  0.01075737  0.00767347  0.00576871  0.00365533  0.00245805  0.00176871  0.00145125  0.00103401  0.0008254   0.00106122  0.00137868  0.0004898 ]
Rango de Señal
[-32768.         -31087.61538462 -29407.23076923 -27726.84615385 -26046.46153846 -24366.07692308 -22685.69230769 -21005.30769231 -19324.92307692 -17644.53846154 -15964.15384615 -14283.76923077 -12603.38461538 -10923.          -9242.61538462  -7562.23076923  -5881.84615385  -4201.46153846  -2521.07692308   -840.69230769    839.69230769   2520.07692308   4200.46153846   5880.84615385   7561.23076923   9241.61538462  10922.          12602.38461538  14282.76923077  15963.15384615  17643.53846154  19323.92307692  21004.30769231  22684.69230769  24365.07692308  26045.46153846  27725.84615385  29406.23076923  31086.61538462  32767.        ]
# SALIDA Grafico de PMF
plt.bar(senalrango,relativa.frequency, width=deltax*0.8)
plt.xlabel('Amplitud de señal')
plt.ylabel('PMF')
plt.show()

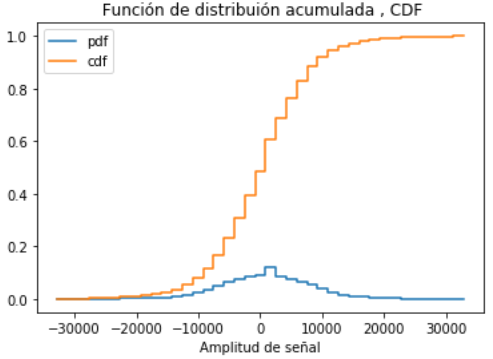
# Función distribución acumulada
acumulada=np.cumsum(relativa.frequency)

# SALIDA CDF
plt.step(senalrango,relativa.frequency,label='pmf', where='post')
plt.step(senalrango,acumulada,label='cdf', where='post')
plt.xlabel('Amplitud de señal')
plt.title(' Función de distribuión acumulada , CDF')
plt.legend()
plt.show()

Para grabar los archivos puede usar np.savetxt(‘nombrearchivo.txt’, arreglodata )