Categoría: Unidades

Referencia: Leon-García 1.3 p.4

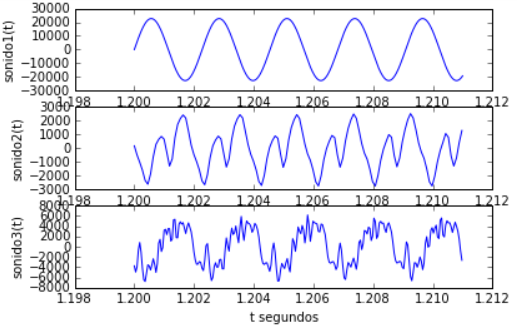
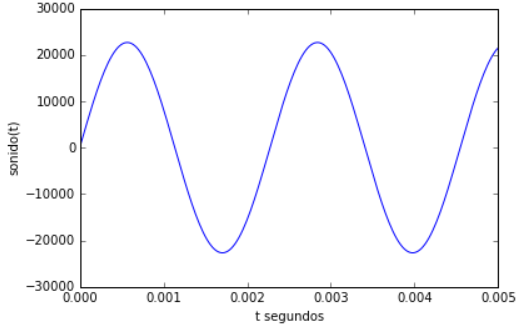
Muchos modelos de señales muestran variaciones impredecibles y un comportamiento aleatorio o probabilístico.

En un experimento aleatorio, repetido sobre las mismas condiciones, entrega resultados que varian de forma poco predecible. Si consideramos realizar un modelos determinístico, encontramos que no es el más apropiado al predecir siempre el mismo resultado.

Experimento aleatorio clásico

En un ánfora se colocan tres pelotas de igual tamaño numeradas con 0, 1 y 2, se agita el ánfora para que no exista un «orden» predeterminado.

Al sacar una pelota cualquiera, no se podría predecir cual será, luego se anota el número de la pelota y se la devuelve al ánfora.

El resultado del experimento, cada vez que se realiza un intento, es un número que pertenece al grupo S={0,1,2}, que formalmente se lo denomina espacio muestral

El resultado del experimento para 20 intentos, se obtiene un vector con los valores siguientes:

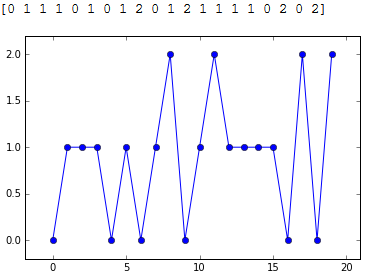
Simulación en Python

Para simular el experimento con python, se puede usar el generador de enteros aleatorios np.random.randint().

# Simulador de Urna con pelotas 0,1,2 
# propuesta: edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt

# INGRESO 
intentos = 20
pelotas  = 3

# PROCEDIMIENTO
aleatorios = np.random.randint(pelotas,size=intentos)

# SALIDA
print(aleatorios)

# grafica
plt.plot(aleatorios,'o-')
plt.xlabel('intentos')
plt.ylabel('aleatorios')
plt.margins(0.1)
plt.show()

# SALIDA - ARCHIVO
archivotxt = 'aleatoriosurna.txt'
np.savetxt(archivo, aleatorios, fmt='%d ')
print(' ... archivo: '+archivotxt+' guardado ...')

Revise la aplicación codificar a morse

Ahora, revise el resultado obtenido al codificar un mensaje cualquiera en morse, y realice sus observaciones:

codigo morse :
'. ... .--. --- .-.. .. -- .--. ..- .-.. ... .- 
 -. -.. --- .-.. .- ... --- -.-. .. . -.. .- -..
 -.. . .-.. -.-. --- -. --- -.-. .. -- .. . -. -
 --- ' 

1. ¿Cuál sería el conjunto posible de resultados?
2. defina el espacio muestral S

Si diseña un equipo para transmitir el tono «la» de 440Hz, debe tomar en cuenta que no siempre es posible obtener una expresión matemática «sencilla» de una señal.

Escuche los siguientes sonidos, vea sus gráficas y realice sus observaciones:

440Hz_44100Hz_16bit_05sec.wav

440Hz_piano.wav

440Hz_violin_A4.wav

• • • • Proponga algunas expresiones matemáticas para cada una de las graficas mostradas.
      • ¿Que tienen en común cada una de las señales?
      • ¿Que tienen de diferente?

Algoritmo en Python

Para obtener la gráfica de los sonidos, se leen los datos y frecuencias de muestreo de cada uno de los archivos.wav

# Señales analógicas
import numpy as np
import matplotlib.pyplot as plt
import scipy.io.wavfile as waves

# INGRESO
archivo1 = '440Hz_44100Hz_16bit_05sec.wav'
[muestreo1, sonido1] = waves.read(archivo1)

archivo2 = '440Hz_piano.wav'
[muestreo2, sonido2] = waves.read(archivo2)

archivo3 = '440Hz_violin_A4.wav'
[muestreo3, sonido3] = waves.read(archivo3)

# SALIDA - Observacion intermedia
print('archivo, frecuencia , dimensiones:')
print('sonido1: ', muestreo1, np.shape(sonido1))
print('sonido2: ', muestreo2, np.shape(sonido2))
print('sonido3: ', muestreo3, np.shape(sonido3))

con lo que se obtiene:

archivo, frecuencia , dimensiones:
sonido1:  44100 (220500,)
sonido2:  11025 (16538,)
sonido3:  22050 (98160,)

Nota: si el archivo.wav tiene etiquetas, se descartan para el ejercicio. por lo que se presenta una advertencia «WavFileWarning».

c:\python34\lib\site-packages\scipy\io\wavfile.py:179: WavFileWarning: Chunk (non-data) not understood, skipping it.
  WavFileWarning)

Se observa que:

• todos los «sonidos» son monofónicos,
• las frecuencias de muestreo de cada archivo son diferentes
• las dimensiones de cada «sonido» o cantidad de muestras indican una duración diferente

Se recomienda escuchar nuevamente cada sonido y decidir el intervalo de observación para las gráficas. Se propone usar una ventana de observación o fragmento desde de los 1.2 segundos por 11 milisegundos.

Se extraen los fragmentos de cada sonido y se determinan los tiempos a los que corresponden basados en cada dt, con lo que se grafican los fragmentos.

# PROCEDIMIENTO
# ventana de observación
inicia  = 1.2
termina = 1.211
canal   = 0

# Extraen los fragmentos de sonido
dt1 = 1/muestreo1
t1  = np.arange(inicia,termina,dt1)
muestras   = len(t1)
fragmento1 = sonido1[int(inicia/dt1):int(inicia/dt1)+muestras]

dt2 = 1/muestreo2
t2  = np.arange(inicia,termina,dt2)
muestras   = len(t2)
fragmento2 = sonido2[int(inicia/dt2):int(inicia/dt2)+muestras]

dt3 = 1/muestreo3
t3  = np.arange(inicia,termina,dt3)
muestras  = len(t3)
fragmento3 = sonido3[int(inicia/dt3):int(inicia/dt3)+muestras]

# SALIDA
# grafica
plt.subplot(311)
plt.plot(t1,fragmento1)
plt.ylabel('sonido1(t)')

plt.subplot(312)
plt.plot(t2,fragmento2)
plt.ylabel('sonido2(t)')

plt.subplot(313)
plt.plot(t3,fragmento3)
plt.ylabel('sonido3(t)')
plt.xlabel('t segundos')

plt.show()

Una vez obtenidas las gráficas, realice observaciones adicionales a cada una de las señales de sonido:
1.
2.
3.

Pregunta:
Para la nota musical «la», ejecutada en un violin tradicional tradicional de madera, ¿tendrá la misma forma de señal siempre?.

Considere las siguientes situaciones:
a. Tocada por diferentes músicos
b. en diferentes lugares
c. en diferentes días

---

Tarea

Buscar la nota «La» en otros instrumentos en formato.wav. De ser necesario realizar observaciones adicionales.

Referencia: Lathi 1.3.2 pdf/p.63, Estándar ISO16, Frecuencias de afinación de un piano

Referencia: Lathi 1.3.2 pdf/p.63, Estándar ISO16, Frecuencias de afinación de un piano

Señal determinística, conocida como una señal cuya descripción física es completamente conocida por su forma matemática o gráfica.

Ejemplo: Señal 440 Hz

Es una señal que puede ser escrita de forma determinística como:

x(t)= cos(2\pi f t)

Siendo f=440 Hz

La señal de 440 Hz es usada como la frecuencia referencia para la afinación de todos los instrumentos musicales desde 1936, adoptada por ISO en 1955 y reafirmado en 1975 como ISO16.

Algoritmo en Python – Graficar en dominio del tiempo

El audio del archivo.wav se puede escuchar con windows media player. Para visualizar la forma de señal del archivo.wav, se puede usar python para leer el archivo y graficar la señal en el dominio del tiempo.

El archivo.wav debe encontrarse en el mismo directorio que el archivo .py de python.

# Señales analógicas
import numpy as np
import matplotlib.pyplot as plt
import scipy.io.wavfile as waves

# INGRESO
# archivo = input('archivo.wav a leer: ')
archivo = '440Hz_44100Hz_16bit_05sec.wav'
[muestreo, sonido] = waves.read(archivo)

# SALIDA - Observación intermedia
print('frecuencia de muestreo: ', muestreo)
print('dimensiones de matriz: ', np.shape(sonido))

frecuencia de muestreo:  44100
dimensiones de matriz:  (220500,)

Nota: si el archivo.wav tiene etiquetas, se descartan para el ejercicio. por lo que se presenta una advertencia «WavFileWarning».

c:\python34\lib\site-packages\scipy\io\wavfile.py:179: WavFileWarning: Chunk (non-data) not understood, skipping it. WavFileWarning)

Existen 220500 muestras en el archivo del ejemplo, que en una sola gráfica puede resultar muy denso y poco observable. La gráfica se limitará a una ventana de tiempo del archivo definida en el rango de tiempo por inicio y termina, con valores en el rango de milisegundos.

El rango de la ventana puede cambiarse si es de interés usar otro rango de tiempo.

De las dimensiones de la matriz (220500,), se determina que el audio es de tipo monofónico al tener una sola dimensión. El audio estéreo tiene dimensiones de (n,2).

# PROCEDIMIENTO
# ventana de observación
inicia  = 0
termina = 0.005
canal   = 0

# selecciona datos
dt = 1/muestreo
t  = np.arange(inicia,termina,dt)
muestras = len(t)
fragmento = sonido[int(inicia/dt):int(inicia/dt)+muestras]

# SALIDA
plt.plot(t,fragmento)
plt.ylabel('sonido(t)')
plt.xlabel('t segundos')
plt.show()

Aunque la señal es simple de ver, y oir, la riqueza del sonido de un instrumento corresponde a otros componentes de frecuencia que los hace únicos al oido estando en la misma nota musical.