Referencia: Ross p192, 196-197, 216
(4.1) Pronóstico del clima
Suponga que la posibilidad que llueva mañana depende de las condiciones del estado del clima de hoy. No importa las condiciones de los días anteriores, solo del estado del clima de hoy.
Suponga también que si llueve hoy, entonces lloverá mañana con una probabilidad α, y si no llueve hoy, entonces lloverá mañana con una probabilidad β.
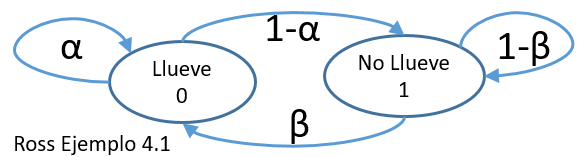
Si se dice que el proceso esta en estado cero cuando llueve y en estado 1 cuando no llueve, entonces el problema se puede realizar con una cadena de Markov de dos estados cuyas probabilidades de transición se encuentran dadas por:
p=\begin{pmatrix} \alpha & 1-\alpha\\ \beta & 1-\beta \end{pmatrix}(4.8) Pronóstico del clima
Considere ahora que α = 0.7 y β = 0.4.
Calcule la probabilidad que lloverá en cuatro días a partir de hoy, dado que está lloviendo hoy.
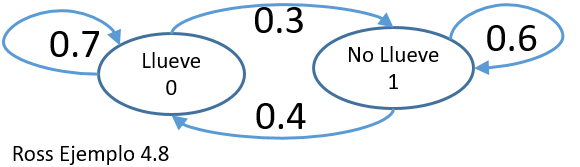
Probabilidad de un paso: solo un día, de hoy a mañana es p
p=\begin{pmatrix} 0.7 & 0.3\\ 0.4 & 0.6 \end{pmatrix}Solución
Transiciones:
Probabilidad en dos dias, pasado mañana: p2
p^{(2)}=\begin{pmatrix} 0.7 & 0.3\\ 0.4 & 0.6 \end{pmatrix} . \begin{pmatrix} 0.7 & 0.3\\ 0.4 & 0.6 \end{pmatrix}
= \begin{pmatrix} 0.61 & 0.39\\ 0.52 & 0.48\end{pmatrix}
Probabilidad en tres dias: p3
Probabilidades en cuatro dias: p4
p^{(4)} = p^{(2)} p^{(2)}
Probabilidad que este lloverá en cuatro días, dado que está lloviendo hoy: p(4)00= 0.5749
El cálculo de la matriz elevado a la potencia n se puede resolver con la instrucción de numpy:
np.linalg.matrix_power(p,n)
import numpy as np # INGRESO p = np.array([[0.7, 0.3], [0.4, 0.6]]) n = 4 # PROCEDIMIENTO pn = np.linalg.matrix_power(p,n) # SALIDA print(pn)
[[ 0.5749 0.4251] [ 0.5668 0.4332]]
Obteniendo nuevamente el resultado p(4)00= 0.5749
(4.20) Las probabilidades al límite o a largo plazo se pueden encontrar escribiendo las ecuaciones para cada πi a partir de la matriz de transición p:
p=\begin{pmatrix} \alpha & 1-\alpha \\ \beta & 1-\beta \end{pmatrix} \pi_0 = \alpha \pi_0 + \beta \pi_1 \pi_1 = (1 - \alpha)\pi_0 + (1 - \beta )\pi_1 \pi_0 + \pi_1 = 1resolviendo con las ecuaciones numeradas como (1), (2) y (3):
usando ecuación (1)
(1-\alpha)\pi_0= \beta \pi_1 \pi_0=\frac{\beta}{1-\alpha} \pi_1usando ecuación (3)
\frac{\beta}{1-\alpha} \pi_1 + \pi_1 =1 \frac{\beta+(1-\alpha)}{1-\alpha} \pi_1 = 1 \pi_1=\frac{1-\alpha}{1+\beta-\alpha}usando la ecuacion (2)
\pi_0=\frac{\beta}{(1-\alpha)} \frac{1-\alpha}{(1+\beta-\alpha)} \pi_0=\frac{\beta}{1+\beta-\alpha}Si α = 0.7 y β = 0.4 como se usaba en el ejemplo anterior, la probabilidad a largo plazo que llueva será:
π0 = 4/7 = 0.571
resultado que también se obtiene en la columna 0 llevando la matriz p(n) a un tiempo n muy grande como en el ejemplo:
import numpy as np # INGRESO p = np.array([[0.7,0.3], [0.4,0.6]]) n = 50 # PROCEDIMIENTO pn = np.linalg.matrix_power(p,n) # SALIDA print(pn)
[[ 0.57142857 0.42857143] [ 0.57142857 0.42857143]]