2. Cadena Markov – Ejemplo: Clima con dos días

Referencia: Ross p.193, 197

(4.4) Pronostico del clima con dos días

Suponga que si llueve o no hoy depende de las condiciones del clima de los dos últimos días.

Si ha llovido en los dos últimos días, entonces que llueva mañana tiene probabilidad de 0.7;
si llovió hoy pero no ayer, entonces que llueva mañana tiene probabilidad de 0.5;
si llovio ayer pero no hoy, entonces que llueva mañana tiene probabilidad de 0.4;
si no ha llovido ni ayer ni hoy, entonces que llueva mañana tiene probabilidad de 0.2

Solución propuesta

Se puede hacer un modelo de cadena de Markov haciendo que el estado del clima mañana sea determinado por las condiciones de hoy y ayer:

Estado 0: si ha llovido hoy y ayer
Estado 1: si ha llovido hoy pero no ayer
Estado 2: Si ha llovido ayer pero no hoy
Estado 3: si no ha llovido ayer y tampoco hoy

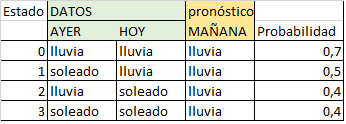
Para considerar los posibles estados añadiendo los valores cuando está soleado, dado que el problema enuncia solo cuando lloverá.

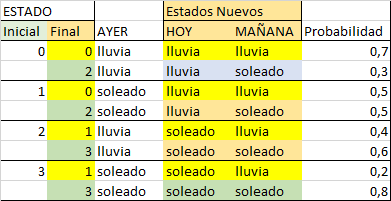
con lo que se puede construir el diagrama de transición de estados:

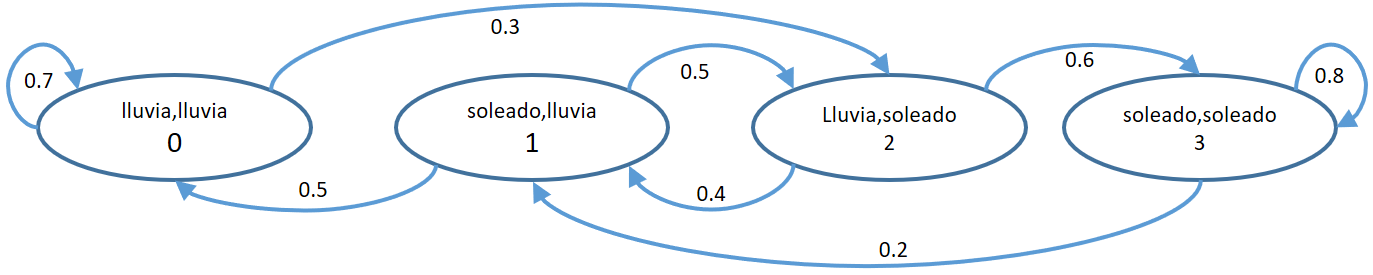
y la matriz de transición es entonces:

p= \begin{pmatrix} 0.7 & 0 & 0.3 & 0 \\ 0.5 & 0 & 0.5 & 0 \\ 0 & 0.4 & 0 & 0.6 \\ 0 & 0.2 & 0 & 0.8 \end{pmatrix}

(4.9) Pronóstico para pasado mañana

Siguiendo con el ejemplo anterior.
Dado que llovió el Lunes y Martes, ¿Cuál es la probabilidad que lloverá el Jueves?

Solución propuesta

La matriz de transición permite hacer el pronóstico hasta el miércoles, para el día jueves es necesario hacer una matriz de dos pasos dada por p⁽²⁾

p^{(2)}= \begin{pmatrix} 0.7 & 0 & 0.3 & 0 \\ 0.5 & 0 & 0.5 & 0 \\ 0 & 0.4 & 0 & 0.6 \\ 0 & 0.2 & 0 & 0.8 \end{pmatrix} \text{.} \begin{pmatrix} 0.7 & 0 & 0.3 & 0 \\ 0.5 & 0 & 0.5 & 0 \\ 0 & 0.4 & 0 & 0.6 \\ 0 & 0.2 & 0 & 0.8 \end{pmatrix}

= \begin{pmatrix} 0.49 & 0.12 & 0.21 & 0.18 \\ 0.35 & 0.20 & 0.15 & 0.30 \\ 0.20 & 0.12 & 0.20 & 0.48 \\ 0.10 & 0.16 & 0.10 & 0.64 \end{pmatrix}

Que llueva el jueves es equivalente no importa si llovió o nó el miércoles, por lo que para la probabilidad del jueves se usa la probabilidad de la fila para estado 0, sumando si llovió o no el miércoles.

p(lloverá jueves|llovió lunes y martes)= p⁽²⁾₀₀+p⁽²⁾₀₁= = 0.49 + 0.12 = 0.61.

Usando python para determinar p⁽²⁾

# 4.9 pronostico para pasado mañana
import numpy as np

# INGRESO
p = np.array([[0.7,   0, 0.3, 0  ],
              [0.5,   0, 0.5, 0  ],
              [  0, 0.4,   0, 0.6],
              [  0, 0.2,   0, 0.8]])

#PROCEDIMIENTO
p2 = np.linalg.matrix_power(p,2)

# SALIDA
print(p2)
print('Para el jueves:', p2[0,0]+p2[0,1])

[[ 0.49  0.12  0.21  0.18]
 [ 0.35  0.2   0.15  0.3 ]
 [ 0.2   0.12  0.2   0.48]
 [ 0.1   0.16  0.1   0.64]]
Para el jueves: 0.61