Referencia: Leon-Couch, 3–8 Modulación Delta, p.192 ; Delta-sigma_modulation Wikipedia, Sigma-Delta – Modulación
La señal de entrada para el decodificador es la señal codificada en los archivo.txt del ejemplo anterior:
deltasigma_datos.txt, deltasigma_parametros.txt
Los archivos para ser leidos deben copiarse al directorio donde se encuentra el algoritmo.py.
Los parametros obtenidos del archivo.txt son:
- ΔY = deltaY = datos[1]
- Δt = datos[0]
- muestras en el rango de observación: k como tamaño del arreglo yentrada.
% matplotlib inline
# Modulacion Sigma-Delta Decodificador
# entrada y[n], salida: x[n]
# propuesta:edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import scipy.io.wavfile as waves
# INGRESO - Lectura de datos desde archivos
# archivoparam = intput('archivo.txt de parametros: ')
# archivodatos = input('archivo.txt de datos: ')
# arhivoaudio = input('archivo.wav a grabar: ')
archivoparam = 'deltasigma_parametros.txt'
archivodatos = 'deltasigma_datos.txt'
archivoaudio = 'sigmadeltaaudio.wav'
param = np.loadtxt(archivoparam,dtype=float)
yentrada = np.loadtxt(archivodatos,dtype=int)
Decodificar la señal +1 y -1 en el vector yentrada consiste en acumular los valores de la secuencia en xdigital usando escalones de tamaño deltaY.
Se procede de forma semejante para los tiempos td usados para el eje de las abscisas usando pasos deltaT.
# PROCEDIMIENTO
deltaT = param[0] # Tamaño delta en eje tiempo
deltaY = param[1] # Tamaño delta en eje Y
k = len(yentrada) # número de muestras
xdigital = np.zeros(k, dtype='int16')
punto = np.zeros(k, dtype=int) # número de muestras
td = np.zeros(k, dtype=float) # tiempo muestreo
# DECOdifica Sigma-Delta
xdigital[0] = yentrada[0]
punto[0] = 0
td[0] = 0
for i in range(1,k):
punto[i] = i
td[i] = deltaT*i
xdigital[i] = xdigital[i-1]+yentrada[i]*deltaY
El resultado puede ser observado en los vectores, en una gráfica de los vectores y en un archivoaudio.wav.
# SALIDA
print('entrada: ')
print(yentrada)
print('salida: ')
print(xdigital)
entrada: [ 0 1 -1 1 -1 1 1 -1 1 -1 1 1 -1 1 -1 1 -1 1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 -1 1 -1 1 -1 1 -1 -1 1 -1 1 -1 -1 1 -1 1 -1 -1 1 -1 1 -1 -1 1 -1 1 -1 -1 1 -1 1 -1 1 -1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 1 -1 1 -1 1] salida: [ 0 6801 0 6801 0 6801 13602 6801 13602 6801 13602 20403 13602 20403 13602 20403 13602 20403 27204 20403 27204 20403 27204 20403 27204 20403 27204 20403 27204 20403 27204 20403 27204 20403 13602 20403 13602 20403 13602 20403 13602 6801 13602 6801 13602 6801 0 6801 0 6801 0 -6801 0 -6801 0 -6801 -13602 -6801 -13602 -6801 -13602 -20403 -13602 -20403 -13602 -20403 -13602 -20403 -27204 -20403 -27204 -20403 -27204 -20403 -27204 -20403 -27204 -20403 -27204 -20403 -27204 -20403 -27204 -20403 -13602 -20403 -13602 -20403 -13602]
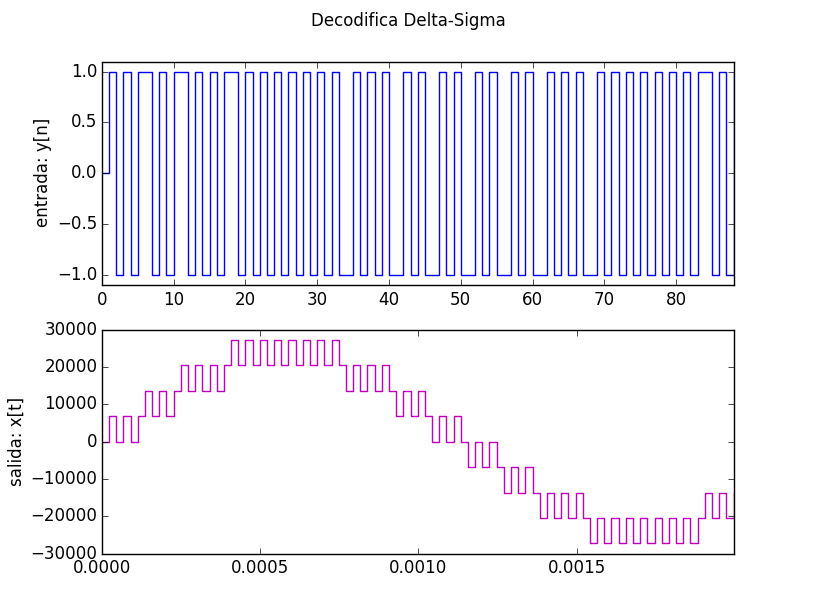
# Graficar
plt.figure(1) # define la grafica
plt.suptitle('Decodifica Delta-Sigma')
plt.subplot(211) # grafica de 2x1 y subgrafica 1
plt.ylabel('entrada: y[n]')
plt.axis((0,k-1,-1.1,1.1)) # Ajusta ejes
plt.step(punto,yentrada, where='post')
plt.subplot(212) # grafica de 2x1 y subgrafica 2
plt.ylabel('salida: x[t]')
xmax = np.max(xdigital)+0.1*np.max(xdigital)# rango en el eje y
xmin = np.min(xdigital)-0.1*np.max(xdigital)
plt.axis((0,td[k-1],xmin,xmax)) # Ajusta ejes
plt.step(td,xdigital, where='post', color='m')
plt.show()
Archivo de Audio del decodificador
Para crear el archivo de audio que permita escuchar el resultado del decodificador, se utiliza una instrucción de scipy que require:
- el nombre del archivoaudio.wav: ‘sigmadeltaaudioruido.wav’
- la frecuencia de muestreo del sonido: muestreo
- el arreglo con la señal digital reconstruida: xdigital
El archivo.wav creado puede ejecutarse con windows media player:
sigmadeltaaudio440Hz_1s.wav
# Salida
# Archivo de audio.wav
muestreo = int(1/deltaT)
waves.write(archivoaudio, muestreo, xdigital)
print(' ... ' + archivoaudio + ' ...')
... sigmadeltaaudio.wav ...