Referencia: Ross problema 8.15 p.570
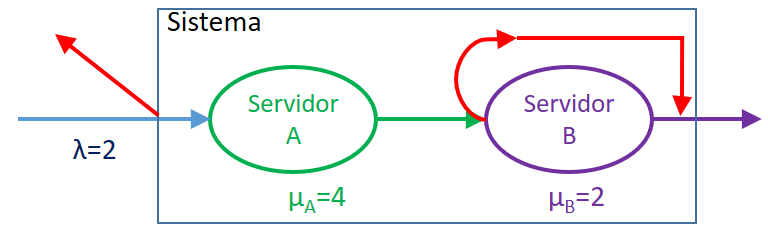
Considere un sistema de servicio secuencial de dos servidores A y B.
Los clientes que llegan entran al sistema solo si el servidor A esta libre.
Si un cliente entra, entonces es atendido inmediatamente por el servidor A.
Cuando la atención del servidor A se completa, el cliente pasa a ser atendido por el servidor B siempre que esté libre, si B esta ocupado, el cliente sale del sistema.
Una vez que el cliente sale del servidor B, el cliente se parte del sistema.
Suponga que las llegadas de cientes son tipo Poisson con tasa de llegada de dos clientes por hora, y que los servidores A y B atienden a tasas exponenciales de cuatro y dos clientes por hora.
a) ¿Cuál es la proporción de clientes que entran al sistema?
b) ¿Cuál es la proporción de clientes que entraron al sistema son atendidos por el servidor B?
c) ¿Cuál es el número promedio de clientes en el sistema?
d) ¿Cuál es el monto promedio de tiempo que un cliente que entró se mantiene dentro del sistema?
Solución
los estados propuestos son:
00 P00
10 P10
01 P01
11 P11
El diagrama de transición entre estados propuesto, considerando de un solo evento por unidad de tiempo:

con lo que se puede plantear las ecuaciones de balanceo («sale=entra»):
2 P00 = 2 P01 4 P10 = 2 P00 + 2 P11 (2+2) P01 = 4 P10 + 4 P11 (4+2) P11 = 2 P01 P00 + P10 + P01 + P11 = 1
Resolviendo:
P00 = P01 ecuación(1) 2 P10 = P00 + P11 (2) P01 = P10 + P11 (3) 3 P11 = P01 (4) P00 + P10 + P01 + P11 = 1 (5)
de la ecuación (2) restando la ecuación (3)
2 P10 - P01 = P00 + P11 - P10 - P11 2 P10 - P01 = P00 - P10 3 P10 - P01 = P00
usando la ecuación (1)
3 P10 - P00 = P00 3 P10 = 2 P00 P10 = 2/3 P00
usando la ecuación (4) y (1)
P11 = (1/3) P01 P11 = (1/3) P00
usando la ecuación (5)
P00 + P10 + P01 + P11 = 1 P00 + P00 + (2/3) P00 + (1/3)P00 = 1 3 P00 = 1 P00 = 1/3
y se obtienen los otros valores para p
P01 = 1/3 P10 = (2/3)(1/3 )= 2/9 P11 = (1/3)(1/3) = 1/9
Con lo que se puede responder:
a) ¿Cuál es la proporción de clientes que entran al sistema?
P00 + P01 = 1/3 + 1/3
= 2/3
c) ¿Cuál es el número promedio de clientes en el sistema?
0*P00 + 1*P10 + 1*P01 + 2*P11 = 0 + 2/9 + 1/3 + 2*1/9 =
= (0+2+3+2)/9 = 7/9
d) ¿Cuál es el monto promedio de tiempo que un cliente que entró se mantiene dentro del sistema?
W = L/λA W = (promedio de clientes en el sistema)/(tasa de los que entran) W= (7/9)/[2(2/3)] = 7/12
Usando Numpy
resolviendo con numpy, se convierten las ecuaciones a matrices, sustituyendo una ecuación con la última (suma de probabilidades =1), se obtiene:
2 P00 = 2 P01 4 P10 = 2 P00 + 2 P11 (2+2) P01 = 4 P10 + 4 P11 (4+2) P11 = 2 P01 P00 + P10 + P01 + P11 = 1
reorganizando:
2 P00 -2 P01 = 0
2 P00 - 4 P10 + 2 P11 = 0
-4 P01 + 4 P10 + 4 P11 = 0
2 P01 - 6 P11 = 0
P00 + P01 + P10 + P11 = 1
se obtienen las matrices A y B para usar con la instrucción solver de numpy:
import numpy as np
A=np.array([
[2,-2,0,0],
[2,0,-4,2],
[0,-4,4,4],
[1,1,1,1]])
B=np.array([0,0,0,1])
p=np.linalg.solve(A,B)
print(p)
[ 0.33333333 0.33333333 0.22222222 0.11111111]
con lo que los valores buscados son:
P00=0.33333333 P01=0.33333333 P10=0.22222222 P00=0.11111111
