Geométrica pmf

Referencia: Gubner p.74, León-García p.102

Variable aleatoria Geométrica

Para 0 ≤ p < 1, se define como una variable aleatoria geométrica₁ que inicia en 1 o estandarizada como:

P(X=k) = (1-p)^{k-1}p k= 1,2,...

Este tipo de variable se usa cuando se pregunta cuántos intentos se requieren de un experimento hasta que se obtenga un resultado específico.

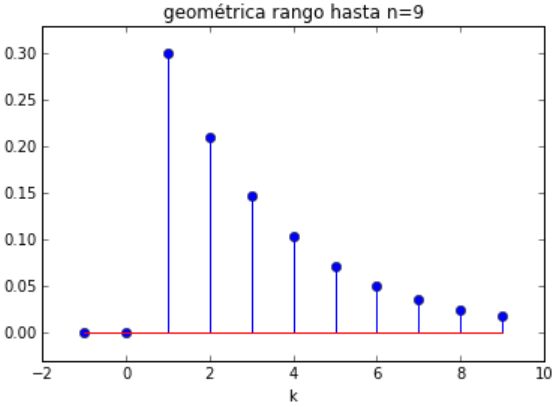
ejemplo de una distribución geométrica₁(p), p=0.3

# Distribución geométrica con valor p
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

# INGRESO
n = 9 
p = 0.3
media = 0

# PROCEDIMIENTO
k  = np.arange(media-1, n+1)
px = stats.geom.pmf(k,p,media)

# SALIDA
print('k: ', k)
print('p(k):', px)

# grafica
plt.title('Uniforme rango hasta n='+str(n))
plt.stem(k,px)
plt.xlabel('k')
plt.margins(0.1)
plt.show()

k:    [-1  0  1  2  3  4  5  6  7  8  9]
p(k): [ 0.         0.          0.3       0.21
        0.147      0.1029      0.07203   0.050421
        0.0352947  0.02470629  0.0172944 ]

Ejemplo

León-García 3.9 p.102
Sea X el número de veces que un mensaje tienen que ser transmitido hasta que sea recibido correctamente en el receptor. Encuentre la pmf de X y la probabilidad que X sea un número par.

X es un variable aleatoria discreta, que toma valores de S_x ={1,2,3,…}. El Evento {X=k} sucede si el experimento principal encuentra las K-1 transmisiones consecutivas con error o fallas seguidas de una sin error o éxito.

p_x(k)= P[X=k] = P[00...01] = (1-p)^{k-1}p = q^{k-1}p \text{para k=1,2,...}

Se puede indicar que X tiene una distribución geométrica.

En la ecuación podemos ver que la suma es 1.

P[\text{X es par}] = \sum\limits_{k=1}^{\infty} p_x(2k) = p\sum\limits_{k=1}^{\infty} q^{2k-1} =p\frac{1}{1-1^2} = \frac{1}{1+q}

Ejemplo: Gubner E2.12 p.74.
Cuando una computadora lee un dato , lo hace primero en la memoria intermedia o caché, en caso de no encontrarla, procede a la memoria RAM.

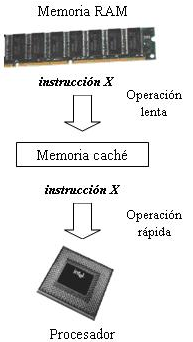
El dato se encuentra en el cache con probabilidad p.

Encuentre la probabilidad que la primera vez que no se encuentra el dato en la memoria intermedia o caché ocurre en la k-ésisma lectura.

Suponga que la presencia del dato en el caché es independiente en cada lectura.

Solución: Sea T=k si la primera vez que no esta un dato en el cache ocurre en la k-ésima lectura.

Para i=1,2,…,

• sea X_i =1 si la en la i-ésima lectura el dato está en caché
• X_i=0 en otro caso

Entonces P( X_i=1) = p y p( X_i=0)=1-p.

La buscado es la primera lectura en que el cache no contiene el dato, es decir la k-ésima lectura, las primeras k-1 tenían el dato en cache.

En términos de eventos:

\{T=k\} = = \{X_1=1\}\cap ...\cap \{ X_{k-1}=1\} \cap \{X_k=0\}

dado que X_i es independiente, y tomando las probabilidades en ambos lados de la ecuación:

P(T=k) = = P(\{X_1=1\}\cap ...\cap \{ X_{k-1}=1\} \cap \{X_k=0\} ) = P(X_1=1) ...P(X_{k-1}=1).P(X_k=0) = p^{k-1}(1-p)

Ejemplo

Gubner E2.13 p.75
Continuando con el ejercicio anterior, ¿Cuál es la probabilidad que la primera lectura fallida en caché sea después de la tercera lectura de memoria?

Solución: Se requiere encontrar:

P(T>3) = \sum\limits_{k=4}^{\infty} P(T=k)

Sin embargo dado que P(T=k) =0 para k≤0, se puede reescirbir en una serie finita:

P(T>3) = 1-P(T \leq 3) = \sum\limits_{k=1}^{3} P(T=k) = 1-(1-p)[1+p+p^2]