Referencia: Código Morse Wikipedia, Recommendation ITU-R M.1677-1 (10/2009) International Morse code, Leon-Couch, 5–9 Señalización Pasabanda Modulada Binaria (OOK)
Morse – Decodificador de sonido de Un simbolo
Analisis de archivo.wav en python
Para analizar el sonido de un símbolo Morse, se inicia por recordar la duración de cada símbolo:
- un punto
'.', cuenta como una marca : morsetonopunto.wav - una raya
'-'dura 3 marcas : morsetonoraya.wav - espacio
' ', que separa una palabra, dura una marca : morsetonoespacio.wav - una pausa se intercala al final del cada símbolo convertido a un tono.
Para la detección de un tono, se revisa la frecuencia activa en varios intervalos de tiempo o ventanas.
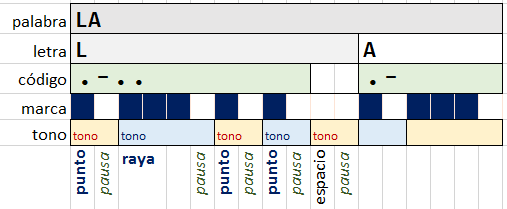
Al contar el número de intevalos (marcas) que aparece un tono vs. el número de intervalos de pausa, se podrá determinar si el sonido corresponde a un punto, una raya o un espacio. Es el proceso contrario a lo realizado para crear el tono, contanto las marcas, la relacion entre marcas y pausas indicará el símbolo recibido.
Algoritmo en python
El sonido para el análisis se obtiene de un archivo.wav, creado con el generador de tonos para un punto '.' o raya '-'. La lectura del archivo proporciona los datos de sonido, y frecuencia de muestreo.
Para el análisis, se supondrá que la ventana tiene la mitad de la duración de un punto, para el ejercicio es 0.04 segundos. Así, una ventana tiene la mitad de muestras que una marca '.' o pausa, obteniendo al menos dos ventanas por cada punto o pausa y tres ventanas por cada raya. Se cuentan las ventanas que tienen sonido o pausa y se comparan para determinar el símbolo.
Que existan al menos dos ventanas por cada punto tienen relación con el muestreo de Nyquist.
Lo expuesto se prueba primero analizando solo una ventana:
# Código Morse - Determina un simbolo a partir de UN sonido # propuesta: edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt import scipy.io.wavfile as waves import scipy.fftpack as fourier # INGRESO # archivo = input('nombre del archivo: ') # archivo = 'morsetonopunto.wav' archivo = 'morsetonoraya.wav' muestreo, sonido = waves.read(archivo) # PROCEDIMIENTO duracion = 0.04 # segundos de un punto partes = 2 # divisiones de un punto # Extraer ventanas para espectro por partes tventana = duracion/partes mventana = int(muestreo * tventana) # muestras de una ventana
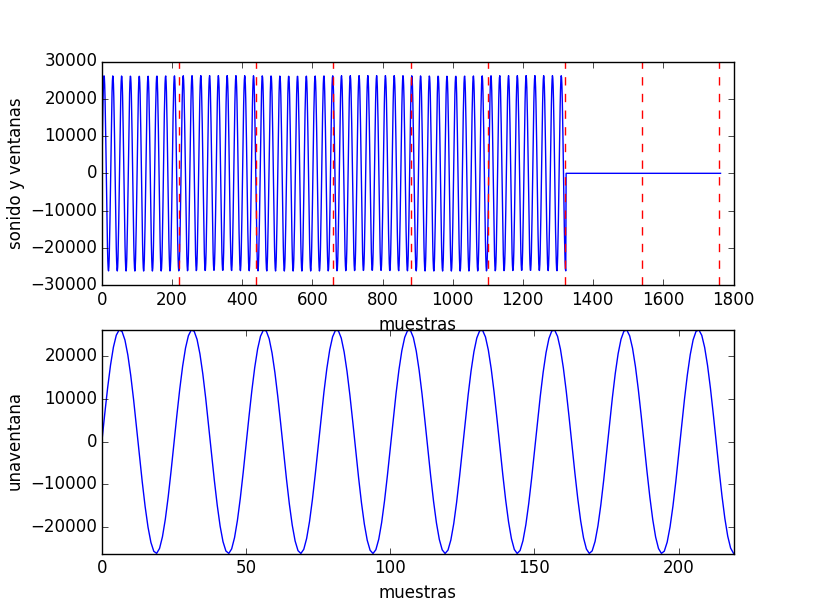
# Observacion intermedia unaventana = sonido[0:mventana] # SALIDA GRAFICA print('muestreo:', muestreo) print('muestras en sonido', len(sonido)) print('intervalo de ventana: ', tventana) print('muestras por ventana: ', mventana) plt.figure(1) plt.subplot(211) plt.plot(sonido, label='sonido') plt.xlabel('muestras') plt.ylabel('sonido y ventanas') k = 1 for i in range(0,int(len(sonido)/mventana)): plt.axvline(x=k*mventana, color='r', linestyle='--') k = k + 1 plt.subplot(212) plt.plot(unaventana) plt.xlabel('muestras') plt.ylabel('unaventana') plt.margins(0) plt.show()
muestreo: 11025 muestras en sonido 1764 intervalo de ventana: 0.02 muestras por ventana: 220
Análisis de una ventana
Para determinar si existe un tono en una ventana, se analiza la existencia de una señal observada en el dominio de la frecuencia.
En el dominio de la frecuencia se requiere usar la «Transformada de Fourier» de la señal en la ventana. La Transformada rápida de Fourirer fft() se encuentra disponible en las librerias «scipy» y el rango de frecuencias para la gráfica se obtiene con fftfreq().
En el resultado se busca la frecuencia (np.argmax()) con mayor magnitud (np.abs()) y se determina si corresponde al «tono» morse esperado.
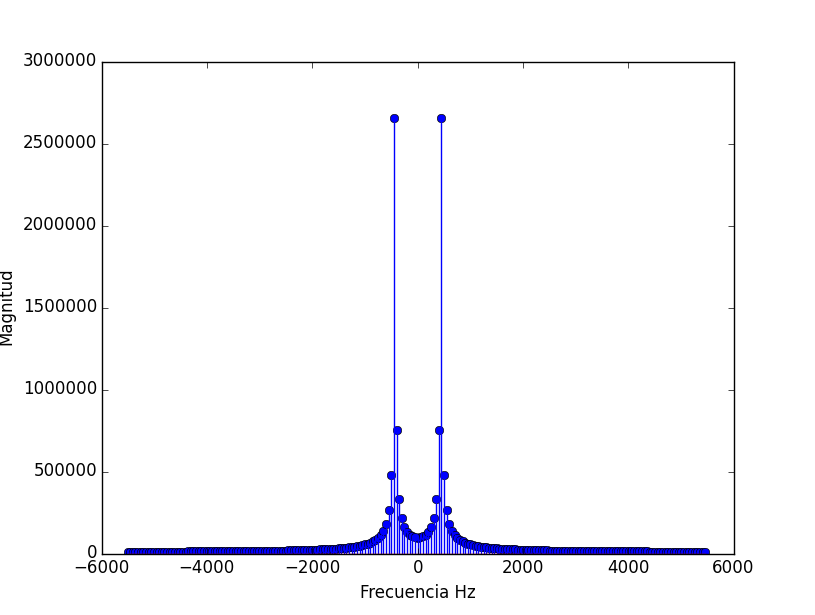
# Espectro de Fourier de una ventana [0:nventana] xf = fourier.fft(unaventana) xf = np.abs(xf) # magnitud de xf tono = np.argmax(xf) # tono en donde # frecuencias para eje frq = fourier.fftfreq(mventana, 1/muestreo ) # SALIDA GRAFICA /Observacion intermedia print('frecuencia tono (Hz): ',frq[tono]) plt.figure(2) plt.xlabel('Frecuencia Hz') plt.ylabel('Magnitud') plt.stem(frq,xf) plt.show()
frecuencia tono (Hz): 451.022727273
Analisis del archivo.wav de un símbolo Morse
Para analizar todo el archivo de sonido, los datos se segmentan por «ventanas» en una matriz, cada fila corresponde a las muestras de una ventana de tiempo.
La matriz debe ser rectangular, por lo que es necesario confirmar que el número de muestras por ventana sean iguales. En caso de no ser así, se realiza un ajuste del ancho del sonido para que el numero de muestras en el archivo sea múltiplo del número de muestras por ventana.
Observar el resultado de crear varias ventanas de tiempo, es semejante a tener un cuaderno en el que cada hoja tiene una imagen con los valores de la señal en cada ventana.
# Ajuste de muestras de ventanas para matriz antes = len(sonido) anchosonido = int(len(sonido)/mventana)*mventana sonido = np.resize(sonido,anchosonido) ventanas = np.reshape(sonido,(-1,mventana)) # -1 indica que calcule las filas # SALIDA print('muestras en sonido: ', antes) print('muestras recortadas a: ', anchosonido) print('ventanas: ') print(ventanas)
muestras en sonido: 1764 muestras recortadas a: 1760 ventanas: [[ 0 6504 12602 ..., -22161 -24942 -26163] [-25748 -23722 -20212 ..., 9594 3241 -3315] [ -9663 -15408 -20188 ..., 25762 26158 24919] ..., [-15377 -9629 -3278 ..., -9733 -15468 -20236] [-23738 -25755 -26161 ..., 0 0 0] [ 0 0 0 ..., 0 0 0]]
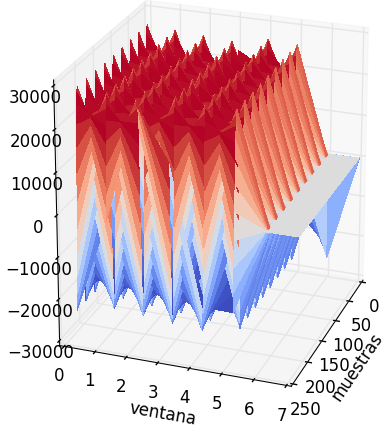
Para observar el resultado se usa una gráfica 3d de superficie.
# Observacion intermedia from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm nfilas,ncolumnas = np.shape(ventanas) x = np.arange(0,ncolumnas) # valores para cada eje y = np.arange(0,nfilas) X, Y = np.meshgrid(x, y) # valores para punto. Z = ventanas # Matriz # Salida, gráfico 3d fig = plt.figure(3,figsize=plt.figaspect(0.5)) ax = fig.add_subplot(1, 2, 1, projection='3d') surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm, linewidth=0, antialiased=False) plt.xlabel('muestras') plt.ylabel('ventana') plt.show()
El proceso de analisis se repite para cada ventana (una fila) en la matriz, guardando cada resultado en un vector «marcas«.
# Analiza con FFT todas las ventanas del sonido filas, columnas = np.shape(ventanas) marcas = np.zeros(filas,dtype=float) # Espectro de Fourier de cada ventana # frecuencias para eje frq = fourier.fftfreq(mventana, 1/muestreo) for fila in range(0,filas,1): xf = fourier.fft(ventanas[fila]) xf = np.abs(xf) # magnitud de xf tono = np.argmax(xf) # tono, frecuencia mayor marcas[fila] = frq[tono]
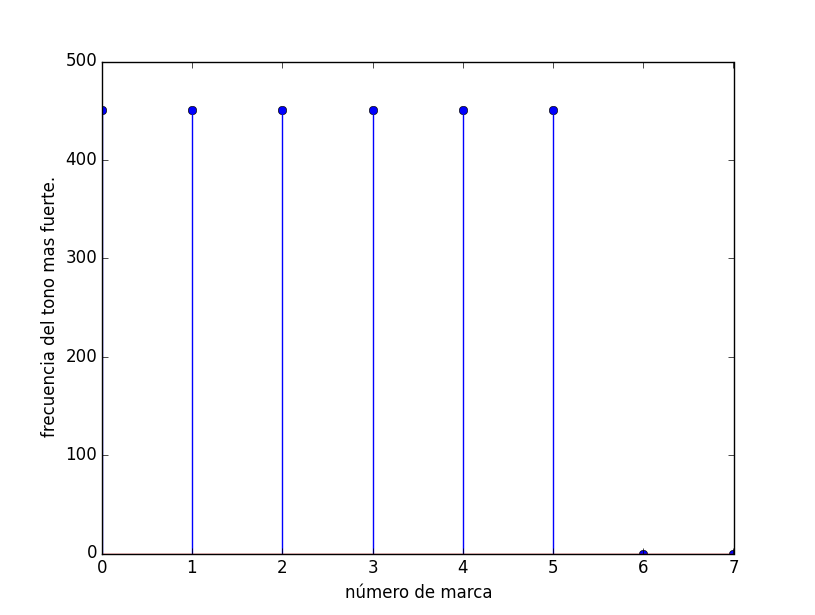
Observamos el resultado en una gráfica 2D.
# SALIDA GRAFICA /Observacion intermedia print(marcas) plt.figure(4) plt.stem(marcas) plt.xlabel('número de marca') plt.ylabel('frecuencia del tono mas fuerte.') plt.show()
[ 451.02272727 451.02272727 451.02272727 451.02272727 451.02272727 451.02272727 0. 0. ]
Para determinar si es punto '.', raya'-' o espacio ' ', se cuentan los noceros y los ceros del arreglo de marcas, la relación entre ellos determina el símbolo que representa el sonido del archivo.wav.
# determina el simbolo noceros = np.count_nonzero(marcas) ceros = len(marcas)-noceros relacion = int(noceros/ceros) if (relacion==3): simbolo = '-' if (relacion==1): simbolo = '.' if (relacion==0): simbolo = 'espacio' # SALIDA print('relacion noceros/ceros:', relacion) print('simbolo morse detectado: ', simbolo)
relacion noceros/ceros: 3 simbolo morse detectado: -
Nota: Observe que cualquier frecuencia en una ventana marca un punto '.'. El detalle es tratado en «Morse – Decodificador del sonido de un mensaje» en : # Busca frecuencia del tono punto.
Programa resumido
El resultado del programa resumido se muestra a continuación:
# Código Morse - Determina un simbolo a partir de UN sonido # propuesta: edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt import scipy.io.wavfile as waves import scipy.fftpack as fourier # INGRESO # archivo = input('nombre del archivo: ') # archivo = 'morsetonopunto.wav' archivo = 'morsetonoraya.wav' muestreo, sonido = waves.read(archivo) # PROCEDIMIENTO duracion = 0.04 # segundos de un punto partes = 2 # divisiones de un punto # Extraer ventanas para espectro por partes tventana = duracion/partes mventana = int(muestreo * tventana) # muestras de una ventana # Ajuste de muestras de ventanas para matriz antes = len(sonido) anchosonido = int(len(sonido)/mventana)*mventana sonido = np.resize(sonido,anchosonido) ventanas = np.reshape(sonido,(-1,mventana)) # -1 indica que calcule las filas # Analiza con FFT todas las ventanas del sonido filas, columnas = np.shape(ventanas) marcas = np.zeros(filas,dtype=float) # Espectro de Fourier de cada ventana # frecuencias para eje frq = fourier.fftfreq(mventana, 1/muestreo) for f in range(0,filas,1): xf = fourier.fft(ventanas[f]) xf = np.abs(xf) # magnitud de xf tono = np.argmax(xf) # tono, frecuencia mayor marcas[f] = frq[tono] # determina el simbolo noceros = np.count_nonzero(marcas) ceros = len(marcas)-noceros relacion = int(noceros/ceros) if (relacion==3): simbolo = '-' if (relacion==1): simbolo = '.' if (relacion==0): simbolo = 'espacio' # SALIDA print('relacion de marcas:', relacion) print('simbolo morse detectado: ', simbolo)
relacion de marcas: 3 simbolo morse detectado: -