Publicado en por Edison Del Rosario

Pdf Bivariada Ejercicio

Referencia: León García Ejercicio 5.16 pag 252

Ejemplo

Encuentre la constante c de normalización y las pdf marginales de la siguiente función:

fX,Y(x,y)={ce−xe−y,0≤y≤x<∞0,otro caso f_{X,Y}(x,y)= \begin{cases} c e^{-x} e^{-y} &, 0\leq y \leq x < \infty \\ 0 & ,\text{otro caso} \end{cases}

Solución

la función es válida en la región mostrada:

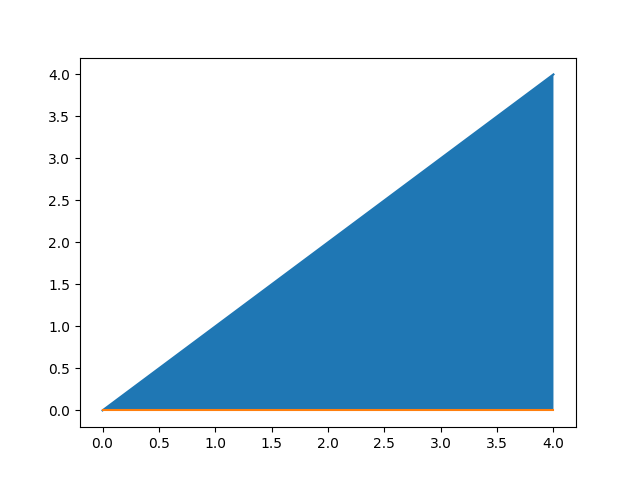
La constante c se encuentra cumpliendo la condición de normalización:

1=∫0∞∫0xce−xe−ydydx= 1 = \int_{0}^{\infty} \int_{0}^{x} c e^{-x} e^{-y} dy dx = =∫0∞ce−x(1−e−x)dx=c2 = \int_{0}^{\infty} c e^{-x} (1-e^{-x}) dx = \frac{c}{2} 1=c2 1 = \frac{c}{2} c=2 c = 2

Determinar las marginales, conociendo que c=2:

fX(x)=∫0∞fX,Y(x,y)dy= f_X (x) = \int_{0}^{\infty} f_{X,Y}(x,y) dy = =∫0x2e−xe−ydy=2e−x∫0xe−ydy= = \int_{0}^{x} 2 e^{-x} e^{-y} dy = 2 e^{-x} \int_{0}^{x} e^{-y} dy = =2e−x[−e−y]∣0x=2e−x[−e−x−(−e0)]= = 2 e^{-x} \left. \left[ - e^{-y} \right]\right|_{0}^{x} = 2 e^{-x} \left[ -e^{-x}-(-e^{0}) \right] = fX(x)=2e−x(1−e−x) f_X (x) = 2 e^{-x} (1- e^{-x}) 0≤x<∞ 0\leq x < \infty
fY(y)=∫0∞fX,Y(x,y)dx= f_Y (y) = \int_{0}^{\infty} f_{X,Y}(x,y) dx = =∫y∞2e−xe−ydx=2e−y∫y∞e−xdx= = \int_{y}^{\infty} 2 e^{-x} e^{-y} dx = 2 e^{-y} \int_{y}^{\infty} e^{-x} dx = =2e−y[−e−x]∣y∞=2e−y[−e−∞−(−e−y)]= = 2 e^{-y} \left. \left[ - e^{-x} \right]\right|_{y}^{\infty} = 2 e^{-y} \left[-e^{-\infty}-(-e^{-y})\right] = =2e−y2e−y = 2 e^{-y} 2 e^{-y} fY(y)=2e−2y f_Y (y) = 2 e^{-2y} 0≤y<∞ 0\leq y < \infty

Tarea: Verificar que las funciones marginales cumplen que el integral es 1

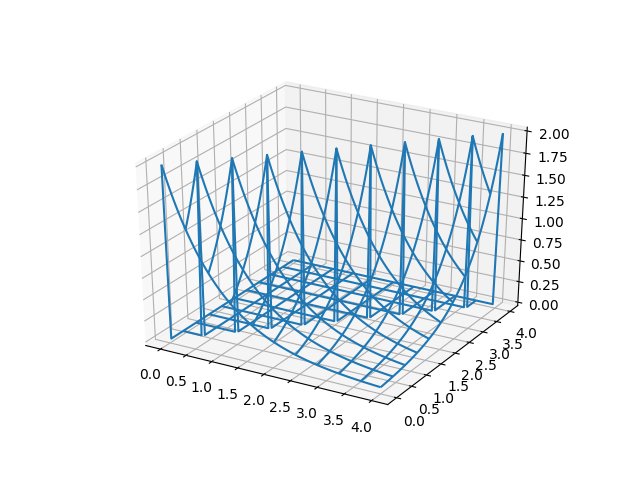
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Función evaluada
def fxydensidad(X,Y):
    n,m =np.shape(X)
    Z=np.zeros(shape=(n,m),dtype=float)
    
    c=2
    for i in range(0,n,1):
        for j in range(0,m,1):
            x=X[i,j]
            y=Y[i,j]
            
            if (y>=0 and y<=x):
                z=c*np.exp(-x)*np.exp(y)
                Z[i,j]=z
    return(Z)

# PROGRAMA ---------

# INGRESO
# Rango de evaluación
xa = 0
xb = 4
ya = 0
yb = 4
# muestras por eje
nx = 500
ny = 500

# PROCEDIMIENTO

# Matriz de evaluación
y = np.linspace(ya,yb,ny)
x = np.linspace(xa,xb,nx)
X,Y = np.meshgrid(x,y)

# Evalúa la función
Z = fxydensidad(X,Y)

# SALIDA
figura  = plt.figure(1)
grafica = figura.add_subplot(1, 1, 1, projection='3d')
grafica.plot_wireframe(X, Y, Z, rstride=10, cstride=10)
plt.show()


# Zona de integración
def arealimite(X):
    n = len(X)
    yinferior = np.zeros(n,dtype=int)
    ysuperior = X
    return(yinferior, ysuperior)

# PROCEDIMIENTO
yinferior, ysuperior = arealimite(x)

# SALIDA
plt.plot(x, yinferior)
plt.plot(x, ysuperior)
plt.fill_between(x, yinferior, ysuperior, where=(ysuperior>=yinferior))
plt.show()


# Forma de las marginales
def marginalx(x):
    fx = 2*np.exp(-x)*(1-np.exp(-x))
    return(fx)

# PROCEDIMIENTO
deltax = (xb-xa)/nx
fx = marginalx(x)
Fx = np.cumsum(fx*deltax)
integrax = np.sum(fx*deltax)

# SALIDA
plt.plot(x,fx, label='f(x)')
plt.plot(x,Fx, label='F(x)')
plt.xlabel('x')
plt.legend()
plt.show()


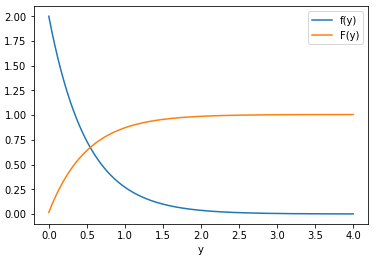
# Forma de las marginales
def marginaly(y):
    fy = 2*np.exp(-2*y)
    return(fy)

# PROCEDIMIENTO
deltay = (yb-ya)/ny
fy = marginaly(y)
Fy = np.cumsum(fy*deltay)
integray = np.sum(fy*deltay)

# SALIDA
print(' El integral sobre el area es: ', integray)

plt.plot(y,fy, label='f(y)')
plt.plot(y,Fy, label='F(y)')
plt.xlabel('y')
plt.legend()
plt.show()