Referencia: Gubner p.70, León-García /p.116

Variable aleatoria Poisson

Una variable aleatoria X se dice que tiene función de probabilidad de masa pmf con parámetro λ>0, definida por:

P_x(k) = \frac {\lambda^k e^{-\lambda}}{k!} k=0,1,2,...

Ejemplo

El número de visitas a un sitio de Internet muy popular en intervalos de 1 minuto se describe con una variable aleatoria tipo Poisson.

Encuentre la probabilidad que se de al menos una visita entre las 3:00 am y 3:01 am si λ=2. Luego encuentre la probabilidad que se realicen al menos 2 visitas durante el mismo intervalo de tiempo.

Solución: Sea X el número de visitas. Entonces:

P(X\geq 1) = 1 - P(X=0) = 1-e^{-\lambda} = 1- e^{-2} \approx 0.865

De forma similar:

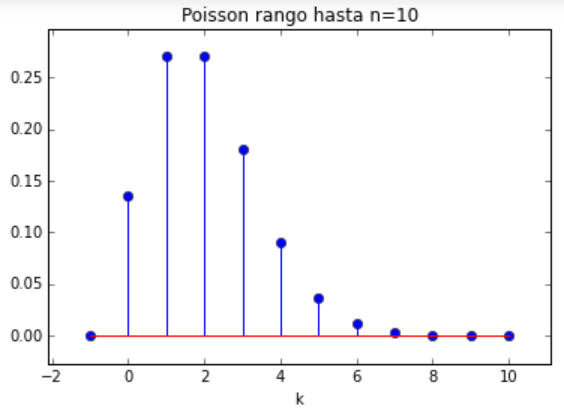
P(X\geq 2) = 1 - P(X=0) - P(X=1) = 1-e^{-\lambda} - \lambda e^{-\lambda} = 1-e^{-\lambda}(1+\lambda) = 1-e^{-2}(1+2) = 0.594

# Distribución Poisson con valor lambda
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

# INGRESO
n = 10
lambd = 2
media = 0

# PROCEDIMIENTO
k  = np.arange(media-1, n+1)
px = stats.poisson.pmf(k,lambd)

# SALIDA
print('k: ', k)
print('p(k):', px)

# grafica
plt.title('Poisson rango hasta n='+str(n))
plt.stem(k,px)
plt.xlabel('k')
plt.margins(0.1)
plt.show()

k:    [-1  0  1  2  3  4  5  6  7  8  9 10]
p(k): [ 0.0000000e+00   1.3533528e-01   2.7067056e-01
        2.7067056e-01   1.8044704e-01   9.0223522e-02
        3.6089408e-02   1.2029803e-02   3.4370865e-03
        8.5927164e-04   1.9094925e-04   3.8189850e-05]