Referencia: León-García p.47, Gubner p.27, Parsen p.41/pdf.62, Ross p.7
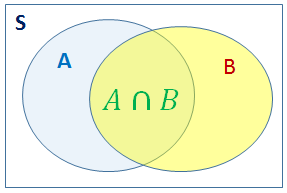
Dos eventos A y B, relacionados de forma que al ocurrir uno, por ejemplo B, se altera la posibilidad de que ocurra el otro, por decir A, lleva a manejar el concepto de probabilidad condicional:
P[A|B] = \frac{ P[A \cap B] }{ P[B] }, \text{para } P[B] > 0Ejemplo :
Una empresa ensambladora de televisores en la ciudad obtiene sus partes de dos proveedores (marca1 y marca2) para reducir el riesgo falla de suministros.
Dado que el proveedor tiene relación directa con la falla de sus equipos, la empresa busca encontrar:
¿cuál proveedor entrega las partes con menor defecto?.
Desarrollo:
Si se analizaron n=1688 televisores para determinar si están buenos o dañados, se resume que:
| marca1 | marca2 | |
|---|---|---|
| bueno | 754 | 499 |
| dañado | 221 | 214 |
Observe que la suma de la primera columna es el número de partes de marca1: N[marca1].
La frecuencia relativa de las partes buenas de marca 1 es:
\frac{N[bueno,marca1]}{N[marca1]}Para cada parte existen cuatro posibles resultados:
| marca1 | marca2 | |
|---|---|---|
| bueno | N[bueno, marca1] | N[bueno, marca2] |
| dañado | N[dañado, marca1] | N[dañado, marca2] |
Observe que las frecuencias relativas de las partes buenas de la marca 1 tambien se puede escribir como el cociente de frecuencias relativas:
\frac{N[bueno,marca1]}{N[marca1]} = \frac{\frac{N[bueno,marca1]}{n} }{ \frac{N[Marca1]}{n}}La probabilidad condicional de que se use una parte buena, sabiendo que se ha seleccionado de la marca1 se puede escribir como P[bueno|marca1]
Si A=bueno, B=marca1 y si P(marca1)>0 entonces:
P[A|B] = \frac{P[A \cap B]}{P[B]} P[A \cap B] = P[A|B]P[B]| B | marca2 | |
|---|---|---|
| A | P[A∩B] | N[bueno, marca2] |
| dañado | N[dañado, marca1] | N[dañado, marca2] |
| P[B] |
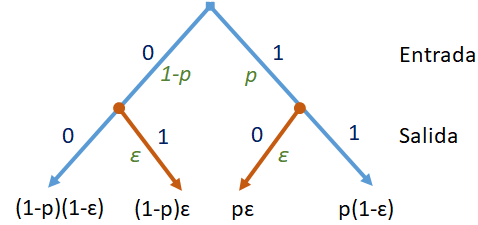
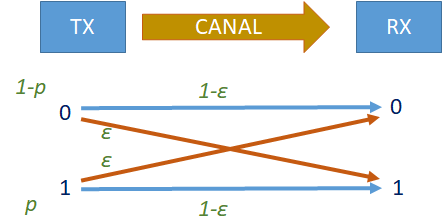
Ejemplo : Sistema de Comunicación Binaria
León-García E2.26 p.50
Los sistemas de comunicación se pueden modelar de la siguiente manera: el usuario ingresa un 0 o un 1 en el sistema y se transmite la señal, luego el receptor detecta la señal transmitida y lo convierte nuevamente en un 0 ó 1.
Suponga que el usuario envia 0´s con probabilidad (1-p) y 1’s con probabilidad p y que al receptor le llegan datos errados con probabilidad ε.
Para cada i=0,1 sea Ai el evento que la «entrada fué i» y sea Bi el evento que lo «recibido en el receptor fue i».
Encuentre las probabilidades P[Ai ∩ Bi] para i=0,1 y j=0,1
| B0 | B1 | |
|---|---|---|
| A0 | (1-p)(1-ε) | (1-p)ε |
| A1 | pε | p(1-ε) |
p[A0 ∩ B0] = (1-p)(1-ε)
p[A0 ∩ B1] = (1-p)ε
p[A1 ∩ B0] = pε
p[A1 ∩ B1] = p(1-ε)
El diagrama de árbol para el sistema es: