Referencia: Gubner 7.1 p 287, León García 5.2 p234, Ross 2.5 p44
Probabilidades conjuntas y marginales
- Un canal telefónico con una señal X presenta un ruido aditivo Y: X+Y
- En un canal inalámbrico la señal X es afectada por un desvanecimiento o ruido multiplicativo: XY
- Si X y Y son las tasas de tráfico de dos routers en un proveedor de Internet, se busca mantener la tasas en valores menores a la capacidad del router : max(X,Y)≤μ
- Sean X y Y los voltajes de un sensor, y se quiere activar una alarma si al menos uno de los voltajes cae por debajo del umbral v: min(X,Y)≤v
Pares de variables aleatorias discretas
Ejemplo:
León-García 5.5. Un switch de datos, tiene dos puertos de entrada y dos puertos de salida. En cualquier instante de tiempo, un paquete llega a cada puerto con probabilidad de 1/2, lo que es equitativamente probable que sea enviado por el puerto 1 o 2.
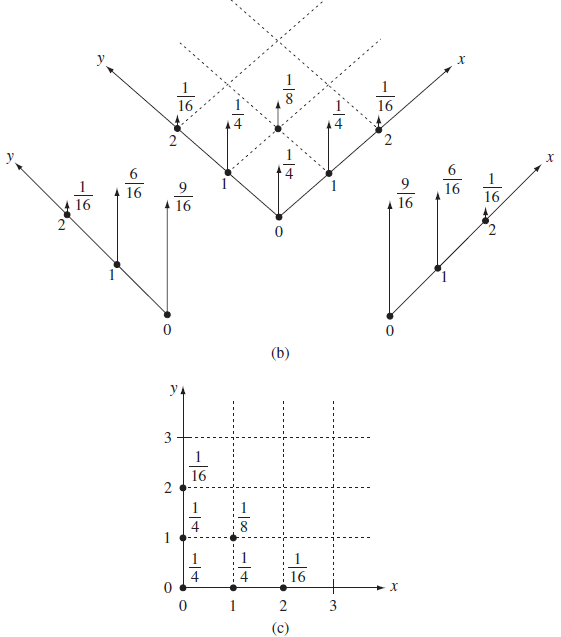
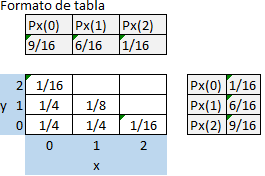
Sea X y Y los números de paquetes destinados para salir por los puertos 1 y 2, respectivamente. Encuentre la pmf de X y Y, mostrando la pmf de forma gráfica.
Solución: La salida Ij para una un puerto de entrada j, puede tomar los siguientes valores:
-
- «n», que no llegue un paquete al puerto de entrada. probabilidad de 1/2
- «a1», llega un paquete con destino de salida puerto 1. con probabilidad de 1/4
- «a2». llega un paquete con destino de salida puerto 2. con probabilidad de 1/4
El espacio muestral S relacionado, consiste de los resultados en pareja de entrada ζ =(I1, I2), El mapeo para cada (X,Y) se muestra en la tabla siguiente:
| ζ | X,Y |
| (n,n) | (0,0) |
| (n,a1) | (1,0) |
| (n,a2) | (0,1) |
| (a1,n) | (1,0) |
| (a1,a1) | (2,0) |
| (a2,a2) | (1,1) |
| (a2,n) | (0,1) |
| (a2,a1) | (1,1) |
| (a2,a2) | (0,2) |
la pmf de (X,Y) es entonces:
pX,Y (0,0) = P[ζ = (n,n)] = 1/2*1/2 = 1/4
pX,Y (0,1) = P[ζ ∈ {(n,a2), (a2,n)}] = 2*1/8 = 1/4
las gráficas de las cdf son: