Proceso pasos aleatorios-caminata aleatoria

Ejemplo: Caminata de pasos aleatorios o Random Step Process

Referencia: Leon-García. E9.14 p.500

Un contador «up-down» o «sube-baja» genera pulsos +1 ó -1. La entrada del contador está dada por D_n = 2 I_n-1, donde I_n es un proceso aleatorio tipo Bernoulli.

D_n = \begin{cases} +1 & \quad \text{, } I_n = 1\\ -1 & \quad \text{, } I_n = 0 \end{cases}

Por ejemplo D_n representaría el cambio en la posición de una partícula que se mueve a lo largo de una linea recta, y cambia entre ±1 cada unidad de tiempo. Ej: n=20, p=0.5

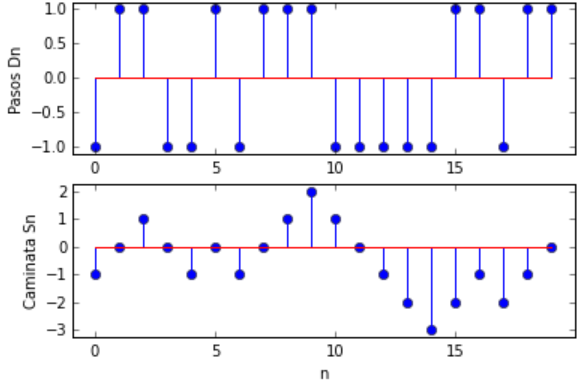
La media de D_n es:

mD(n) = E[Dn] 
    = E[ 2In -1] = 2E[In]-1
    = 2p - 1

La varianza de D_n se encuentra como:

VAR[Dn] = VAR[2In - 1]
    = 22 VAR[In]
    = 4p(1 - p)

Las probabilidades de los eventos de D_n se calculan como en el ejemplo del tema de la Binomial.

---

Instrucciones en Python

# Proceso caminata de pasos aleatorios
# Leon-Garcia E 9.14 p.500
# propuesta: edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

# INGRESO
# n=int(input('cuantos aleatorios: '))
# p=float(input('probabilidad p: '))
n = 20
p = 0.5

# PROCEDIMIENTO

# inicializa vectores
pasos  = np.zeros(n, dtype=int)
camina = np.zeros(n, dtype=int)
ejex   = np.zeros(n, dtype=int)

s = 0 
for i in range(0,n):
    # genera aleatorio con binomial
    pasos[i] = 2*(stats.binom.rvs(1,p))-1
    s = s+pasos[i]
    camina[i] = s
    ejex[i]   = i

# SALIDA
# grafica pasos 
plt.subplot(211)
plt.stem(ejex,pasos)
plt.ylabel('Pasos Dn')
plt.margins(0.05)

# grafica caminata aleatoria
plt.subplot(212)
plt.stem(ejex,camina)
plt.ylabel('Caminata Sn')
plt.margins(0.05)
plt.xlabel('n')

plt.show()

Referencia: León-García 9.14 p.500-501