Un proceso aleatorio o proceso estocástico es una familia de variables aleatorias.
Por ejemplo, al enviar una secuencia de bits sobre un canal inalámbrico, no existe un grupo predeterminado de bits a transmitir, que para modelar se usa una secuencia infinita de variables aleatorias.
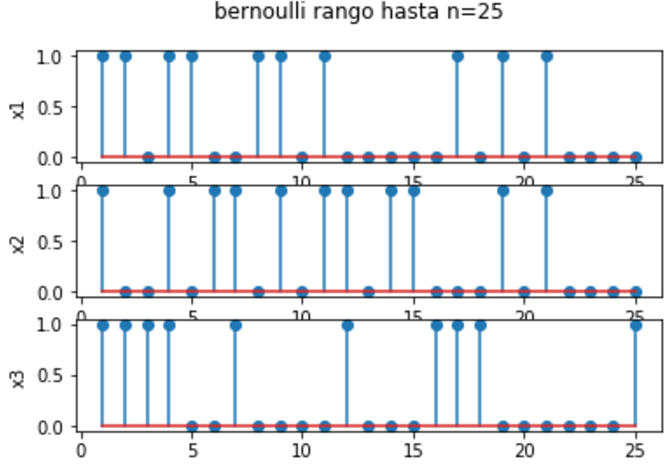
Tres realizaciones de X1, X2, ... se obtienen como:
Instrucciones en Python
# secuencia de bits (trama) # propuesta: edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt import scipy.stats as stats # ingreso n = 25 p = 0.5 # PROCEDIMIENTO # indice k k = np.arange(1, n+1) # genera muestras de variable aleatoria con bernoulli x1 = stats.bernoulli.rvs(p, size=n) x2 = stats.bernoulli.rvs(p, size=n) x3 = stats.bernoulli.rvs(p, size=n) # SALIDA plt.suptitle('bernoulli rango hasta n='+str(n)) # grafica X1 plt.subplot(311) plt.stem(k,x1) plt.ylabel('x1') plt.margins(0.05) # grafica X2 plt.subplot(312) plt.stem(k,x2) plt.ylabel('x2') plt.margins(0.05) # grafica X3 plt.subplot(313) plt.stem(k,x3) plt.ylabel('x3') plt.margins(0.05) plt.xlabel('k') plt.show()
Procesos discretos en el tiempo
Un proceso aleatorio discreto en el tiempo es una familia de variables aleatorias {Xn}, donde a partir de n se define en un subgrupo de enteros.
Por ejemplo:
{Xn, n=1, 2, ...}
{Xn, n=0, 1, 2, ...}
{Xn, n=0, ± 1 , ± 2 ...}
Recordando que las variables aleatorias son funciones definidas en un espacio muestral S, se puede pensar en Xn(ω) en dos formas:
-
- Para n fijos, Xn(ω) es función de ω y por lo tanto una variable aleatoria.
- Para ω fija, se obtiene una secuencia de números X1(ω), X2(ω), X3(ω), ... . Secuencia que se denomina una realización, camino muestral, o función muestral del proceso aleatorio.
Ejemplo: Envío de bits sobre un canal con ruido
Referencia: Gubner 10.1 pdf/p.383
Enviar una secuencia de bits sobre un canal con ruido , los bits se invierten de forma independiente con probabilidad p.
Sea:
-
-
-
- Xn(ω)=1 si se invierte el n-ésimo bit y
- Xn(ω)=0 de otra forma.
-
-
entonces {Xn(ω), n= 1, 2, ...} es una secuencia Bernoulli(p) i.i.d .
Tres realizaciones del ruido se reprerentan en la gráfica del ejercicio anterior. Sin embargo, el resultado de la señal Xn afectada por el Ruidon como se vería en el receptor se muestra a continuación.
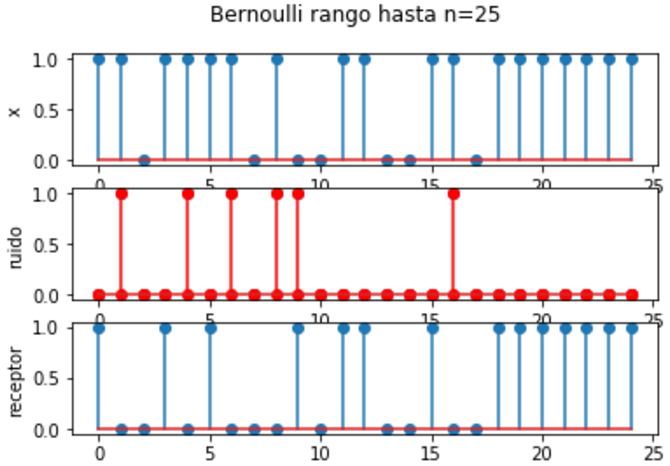
# Ejercicio: Envío de bits sobre un canal con ruido # Gubner 10.1 # propuesta: edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt import scipy.stats as stats # INGRESO n = 25 pcanal = 0.5 p = 0.2 # error o inversión de bit # PROCEDIMIENTO # muestras k k = np.arange(1, n+1) # transmisor x = stats.bernoulli.rvs(pcanal, size=n) # ruido del canal ruido = stats.bernoulli.rvs(p, size=n) # En el receptor receptor = np.zeros(len(x), dtype = int) for i in range(0,len(x)): if (ruido[i] == 0): receptor[i] = x[i] if (ruido[i] == 1): # invierte el bit if (x[i] == 1): receptor[i] = 0 if (x[i] == 0): receptor[i] = 1 # SALIDA plt.suptitle('Bernoulli rango hasta n='+str(n)) # trama de bits en transmisor plt.subplot(311) plt.stem(k,x) plt.ylabel('x') plt.margins(0.05) # ruido del canal plt.subplot(312) plt.stem(k,ruido,markerfmt='or') plt.ylabel('ruido') plt.margins(0.05) # Señal recibida en receptor plt.subplot(313) plt.stem(k,receptor) plt.ylabel('receptor') plt.margins(0.05) plt.xlabel('k') plt.show()
Procesos contínuos en el tiempo
Un proceso aleatorio contínuo en el tiempo es una familia de variables aleatorias {Xt} donde t esta definido en un intervalo de tiempo.
{Xt, t ≥ 0}
{Xt, 0 ≤ t ≤ T}
{Xt, -∞ ≤ t ≤ ∞}
Ejemplo: Portadora con fase aleatoria
Referencia: Gubner 10.5 pdf/p.386
En radio comunicación, una señal portadora se modela como una sinusoide con fase aleatoria. La razón para usar una fase aleatoria es que en receptor no se conoce cuando se encendió el transmisor o la distancia entre el transmisor y receptor, que son factores que afectan a la fase.
El modelo matemático para éste caso es el proceso aleatorio contínuo en el tiempo, definido por:
xt = cos(2πft + θ)
donde f es la frecuencia de la portadora y θ es una variable aleatoria uniforme [-π, π].
Tres realizaciones del proceso que dan tres valrores dirferenctes de θ y su efecto en la portadora se obtienen como:

# Gubner 10.5 Portadora con fase aleatoria # propuesta: edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt import scipy.stats as stats # ingreso n = 5 f = 1 # PROCEDIMIENTO # muestras ti t = np.arange(0,n,0.1) # genera muestras aleatorias con f: uniforme theta = stats.uniform.rvs(loc=-np.pi, scale=2*np.pi ,size=3) # selales desfasadas xt0 = np.cos(2*np.pi*f*t + theta[0]) xt1 = np.cos(2*np.pi*f*t + theta[1]) xt2 = np.cos(2*np.pi*f*t + theta[2]) # SALIDA print('theta: ',theta) # grafica plt.suptitle('Portadora') # grafica x0 plt.subplot(311) plt.plot(t,xt0) plt.ylabel('x0') plt.margins(0.05) # grafica x1 plt.subplot(312) plt.plot(t,xt1) plt.ylabel('x1') plt.margins(0.05) # grafica x2 plt.subplot(313) plt.plot(t,xt2) plt.ylabel('x2') plt.margins(0.05) plt.xlabel('k') plt.show()
Referencia: Gubner 10 pdf/p.383, León-García 9.1 pdf/p.488