a) Determine el espacio de estados del sistema
"Para los estados utilice la nomenclatura (tp1, tp2), donde tpi corresponde a la cantidad de atención de enlaces tipo i."
Para el caso que λ1>sea positivo y λ2=0
s1 = {00, 10, 20, 30, 40, 50}
Para el caso que λ1=0 y λ2 es positivo
s2 = {01, 02}
Se completan los casos intermedios para usar toda la capacidad
sotros = {11, 12, 21, 31}
El total de Espacios de estados será la union de los tres espacios anteriores:
s = {00, 10, 20, 30, 40, 50, 01, 02, 11, 12, 21,31}
b) Dibuje y etiquete el diagrama de estados del sistema
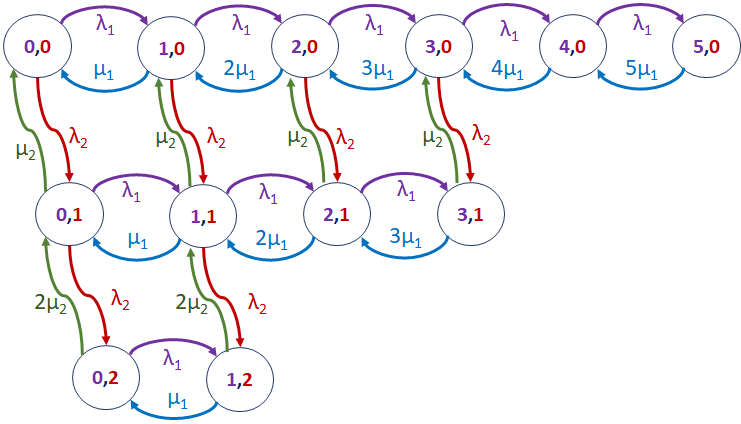
c) Plantee las ecuaciones de estados del sistema
SALE = ENTRA
Primera Fila del diagrama
(λ1 +λ2 ) p00 = µ1p10 + µ2p01
(λ1 +λ2 + µ1) p10 = 2µ1p20 + µ2p11 +λ1p00
(λ1 +λ2 +2µ1) p20 = 3µ1p30 + µ2p21 +λ1p10
(λ1 +λ2 +3µ1) p30 = 4µ1p40 + µ2p31 +λ1p20
(λ1 +4µ1) p40 = 5µ1p40 + +λ1p30
5µ1 p50 = λ1p40
Segunda Fila del diagrama
(λ1 +λ2 + µ2 ) p01 = µ1p11 + 2µ2p02 +λ2p00
(λ1 +λ2 + µ1 +µ2) p11 = 2µ1p21 + 2µ2p12 +λ1p01 +λ2p10
(λ1 +2µ1 +µ2) p21 = 3µ1p31 +λ1p11 +λ2p20
( +3µ1 +µ2) p31 = +λ1p21 +λ2p30
Tercera Fila del diagrama
(λ1 +2µ2) p02 = µ1p12 +λ2p01
(µ1 +2µ2) p12 = λ1p02 +λ2p11
p00 +p10 +p20 +p30 +p40 +p50 +p01 +p11 +p21 +p31 +p02 +p12 =1
d) Determine la probabilidad de pérdidas de conexiones tipo 1 y tipo 2, y la probabilidad de pérdidas del sistema.
Pérdidas de tipo 1 se dan en los estados 12, 31, 50 ptipo1 = p12 + p31 + p50 Pérdidas de tipo 2 se dan en los estados 12, 31, 50, 02, 21, 40 ptipo2 = p12 + p31 + p50 + p02 + p21 + p40
e) ¿Cuál probabilidad de pérdidas es más alta? Para conexiones tipo 1 o 2, describa su respuesta.
Se pierden más conexiones del tipo 2, pues existen más términos en la suma de probabilidades
f) Calcule la utilización del enlace por cada tipo
Se calcula como valor esperado por ocupación de servidores:\rho = \frac{\sum_{i=0}^{5} \sum_{j=0}^{3} p_{ij} (i \text{1MB} + j \text{2MB})}{\text{5MB}}
En el caso que se requieren por tipo de conexión:
\rho_{1} = \frac{\sum_{i=0}^{5} \sum_{j=0}^{3} p_{ij} (i \text{1MB} )}{\text{5MB}}
\rho_{2} = \frac{\sum_{i=0}^{5} \sum_{j=0}^{3} p_{ij} (j \text{2MB})}{\text{5MB}}
