1ra Evaluación I Término 2017-2018. Junio 27, 2017

Tema 1
Cadena de Markov, desarrollo a partir de la matriz

\begin{pmatrix} 1/2 & 1/2 & 0 & 0 \\ 9/10 & 0 & 1/10 & 0 \\ 0 & 1/10& 0 & 9/10\\ 0 & 0 & 1/2 & 1/2 \end{pmatrix}

Diagrama de Estados de transición:

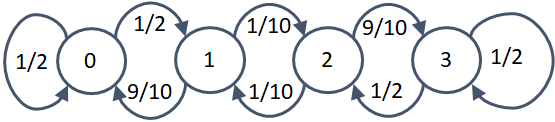
Resolución planteando las ecuaciones

π0 = (1/2)π0 + (9/10)π1
π1 = (1/2)π0 + (1/10)π2
π2 = (1/10)π1 + (1/2)π3
π3 = (9/10)π2 + (1/2)π3
π0 + π1 + π2 + π3 = 1

usando ecuacion (1)
π0 -(1/2)π0 = (9/10)π1
(1/2)π0  = (9/10)π1
π1 = (5/9)π0

usando ecuacion(2)
(5/9)π0 = (1/2)π0 + (1/10)π2
(5/9)π0 - (1/2)π0 = (1/10)π2
[(10 - 9)/18] π0 = (1/10)π2
[1/18] π0 = (1/10)π2
π2 = (10/18) π0
π2 = (5/9) π0

usando ecuacion (3)
(5/9) π0 = (1/10)(5/9)π0 + (1/2)π3
(5/9) π0 - (1/10)(5/9)π0 = (1/2)π3
(1-1/10)(5/9) π0 = (1/2)π3
(9/10)(5/9) π0 = (1/2)π3
(1/2) π0 = (1/2)π3
π3 = π0

usando la ecuación (5)
π0 + (5/9)π0 + (5/9) π0 +  π0 = 1
(1 + 5/9 + 5/9 + 1) π0 = 1
(2 + 10/9) π0 = 1
(28/9) π0 = 1
π0 = (9/28)

π1 = (5/9)(9/28) = 5/28
π2 = 5/28
π3 = 9/28

---

resolución usando numpy de python

# Tema 1. matriz de transición
import numpy as np

p=np.array([
    [ 1/2, 1/2,   0,   0],
    [9/10,   0,1/10,   0],
    [   0,1/10,   0,9/10],
    [   0,   0, 1/2, 1/2]
    ])
n=200
pn=np.linalg.matrix_power(p,n)
print(pn)

# Resolviendo por matrices A= AT-I) y el vector de ceros terminado en 1
k=len(p)
A=p.transpose()
A=A-np.identity(k, dtype=int)
# la última fila se sustituye por la suma de probabilidades
A[-1,:]=np.ones(k,dtype=int)
B=np.zeros(k,dtype=int)
B[-1]=1  # el último
Pncalc=np.linalg.solve(A,B)
print('largo plazo')
print(Pncalc)

[[ 0.32142907  0.17857167  0.17857119  0.32142808]
 [ 0.321429    0.17857164  0.17857122  0.32142814]
 [ 0.32142814  0.17857122  0.17857164  0.321429  ]
 [ 0.32142808  0.17857119  0.17857167  0.32142907]]
largo plazo
[ 0.32142857  0.17857143  0.17857143  0.32142857]

verificando que las fracciones sean los valores encontrados por python:

print(5/28)

0.17857142857142858