1ra Evaluación I Termino 2017 Tema 3.Soluciones propuestas
Tema 3
usamos dos dígitos para representar (operadora,tecnicos) en cantidades de ocupado=0,1,2
Los estados de operadora libre serán: (00),(01),(02)
Los estados de operadora ocupada serán: (10),(11),(12)
Diagrama de Transición
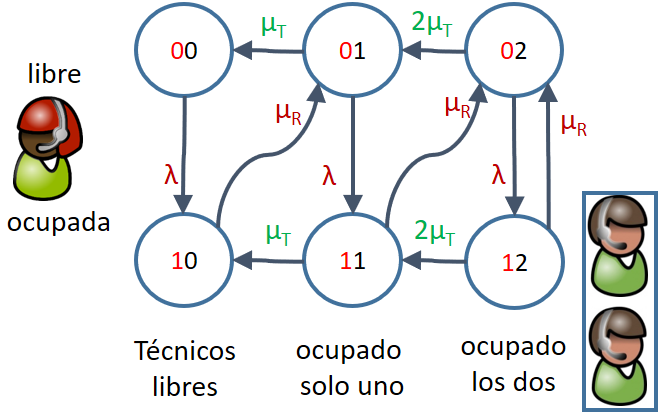
Ecuaciones de Balanceo
λ P00 = μT P01 (μT + λ) P01 = 2 μT P02 + μR P10 (2 μT + λ) P02 = μR P11 + μR P12 μR P10 = λ P00 + μT P11 (μR + μT) P11 = λ P01 + 2 μT P12 (μR + 2 μT) P12 = λ P02 P00 + P01 + P02 + P10 + P11+ P12 = 1 λ = 1/10, μR = 1/3, μT =1/15
reemplazando
1/10 P00 = 1/15 P01 (1/15 + 1/10) P01 = 2 (1/15) P02 + 1/3 P10 (2 (1/15) + 1/10) P02 = 1/3 P11 + 1/3 P12 1/3 P10 = 1/10 P00 + 1/15 P11 (1/3 + 1/15)P11 = 1/10 P01 + 2 (1/15) P12 (1/3 + 2 (1/15)) P12 = 1/10 P02 P00 + P01 + P02 + P10 + P11 + P12 = 1
reordenando para hacer la matriz que resuelve el sistema de ecuaciones:
1/10 P00 - 1/15 P01 = 0
(1/15 + 1/10) P01 - 2 (1/15) P02 - 1/3 P10 = 0
(2 (1/15) + 1/10) P02 - 1/3 P11 - 1/3 P12 = 0
1/10 P00 - 1/3 P10 + 1/15 P11= 0
1/10 P01 - (1/3+1/15) P11 + 2 (1/15) P12 = 0
1/10 P02 - (1/3 + 2 (1/15)) P12 = 0
P00 + P01 + P02 + P10 + P11 + P12 = 1
Resolver usando matrices, en python:
import numpy as np
A=np.array([
[1/10, -1/15, 0, 0, 0, 0],
[ 0,(1/15 + 1/10), -2/15,-1/3, 0, 0],
[ 0, 0,2/15+1/10, 0,-1/3,-1/3],
[1/10, 0, 0,-1/3,1/15, 0],
[ 0, 1/10, 0, 0,-(1/3+1/15),2/15],
[ 1, 1, 1, 1, 1, 1]
])
# Sustituyendo la ultima ecuación por la de suma de probabilidades,
# resolviendo por matrices y usando el vector de ceros excepto el último
k=len(A)
B=np.zeros(k,dtype=int)
B[-1]=1
Pncalc=np.linalg.solve(A,B)
print('A= ')
print(A)
print('B=',B)
print('Solucion P:')
print(Pncalc)
A= [[ 0.1 -0.0666667 0. 0. 0. 0. ] [ 0. 0.1666667 -0.133333 -0.3333333 0. 0. ] [ 0. 0. 0.233333 0. -0.3333333 -0.3333333] [ 0.1 0. 0. -0.3333333 0.0666667 0. ] [ 0. 0.1 0. 0. -0.4 0.1333333] [ 1. 1. 1. 1. 1. 1. ]] B= [0 0 0 0 0 1] Solución P: [ 0.2259007 0.3388510 0.2044791 0.0876339 0.099318 0.0438169]
e) Encuentre la probabilidad que los técnicos estén ocupados.
Ocupados al menos uno e independiente si esta o no ocupada la recepcionista
P01+P02+P11+P12 =
0.33885102 + 0.20447907 + 0.0993184 + 0.04381694 = 0.68646543
f) ¿Cuál es la probabilidad que una llamada se pierda en la recepción?
para ello la operadora tiene que estar ocupada
P10 + P11 + P12 =
0.08763389 + 0.0993184 + 0.04381694 = 0.23076923000000002
g) ¿Cuál es la tasa de clientes satisfechos? (salida del sistema, throughput)
es la tasa de clientes que la operadora logra transferir a los técnicos:
P10 μR + P11 μR =
0.08763389 * (1/3) + 0.0993184 *(1/3) = 0.06231742999999999
o también la tasa ponderada de partida de los atendidos por los técnicos:
P01 μT + P02 2 μT + P11 μT + P12 2μT =
0.33885102*(1/15)+0.20447907*(2/15)+0.0993184*(1/15)+0.04381694 *(2/15) = 0.06231742933333334
