s1Eva_IT2017_T4 Portabilidad numérica

1ra Evaluación I Termino 2017 Soluciones propuestas

Tema 4. Portabilidad Numérica

Tabla de datos:

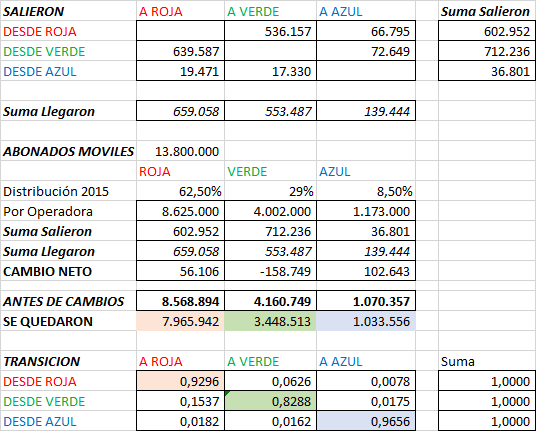
Diagrama de estados

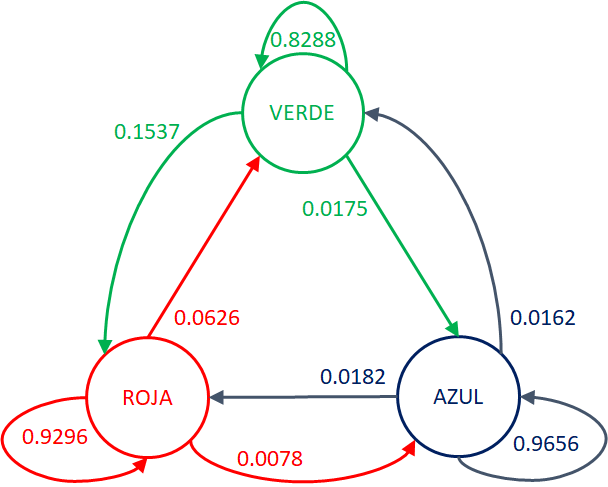
# Tema 4. Portabilidad numérica
import numpy as np

p=np.array([
    [0.9296,0.0626,0.0078],
    [0.1537,0.8288,0.0175],
    [0.0182,0.0162,0.9656]
    ])

e) Suponga que observa un abonado de la operadora ROJA:

1. Determine la probabilidad que en el siguiente periodo sea abonado de VERDE.

Se usa el valor de P_RojaVerde = P₁₂ = 0.0626

2. Luego el cliente del numeral anterior al segundo periodo decida cambiarse a la operadora AZUL

Usar la matriz en P², considerando en dos periodos se cambia AZUL iniciando en Rojo P²₁₃ = 0.01587806

p2=np.linalg.matrix_power(p,2)
print(p2)

[[ 0.87391974  0.1102022   0.01587806]
 [ 0.27058458  0.69681456  0.03260086]
 [ 0.03698258  0.0302086   0.93280882]]

3. Para otro abonado de la operadora ROJA, determine la probabilidad que luego de tres periodos no termine en la operadora VERDE.

Usar la matriz en P³, iniciando en Rojo, puede seguir en Rojo o pasar a Azul P³₁₁ + P³₁₃ = 0.87391974 + 0.01587806 = 0.8897978

también como 1- 0.1102022 = 0.8897978

p3=np.linalg.matrix_power(p,2)
print(p3)
print(0.87391974 +  0.01587806)

[[ 0.87391974  0.1102022   0.01587806]
 [ 0.27058458  0.69681456  0.03260086]
 [ 0.03698258  0.0302086   0.93280882]]
0.8897978

f) Determine las probabilidades de transición a largo plazo.

n=200
pn=np.linalg.matrix_power(p,n)
print(pn)

k=len(p)
A=p.transpose()
A=A-np.identity(k, dtype=int)
A[-1,:]=np.ones(k,dtype=int)
B=np.zeros(k,dtype=int)
B[-1]=1
Pncalc=np.linalg.solve(A,B)
print('largo plazo')
print(Pncalc)

[[ 0.54340383  0.22099379  0.23560237]
 [ 0.54339955  0.2209924   0.23560805]
 [ 0.54332021  0.22096663  0.23571316]]
largo plazo
[ 0.54338318  0.22098708  0.23562973]

g) Para cada uno de los valores encontrados en el literal anterior, con sus palabras describa en una línea el significado referenciado al problema.

largo plazo
[ 0.54338318 0.22098708 0.23562973]

algunos ejemplos:

Representa cómo se distribuyó el mercado a largo plazo, que un abonado pertenezca a una de las operadoras….

el 54,33 % de probabilidad que un abonado sea de la operadora ROJA

el 22,09% de probabilidad que un abonano sea de la operadora VERDE

que en muy largo plazo, la operadora ROJA seguirá siendo el operador dominante
que de mantenerse la tendencia, el operador AZUL solo puede crecer hasta el 23,56% del mercado.
que el operador verde podría seguir perdiendo clientes y disminuir su participación de mercado desde el 29% al 22,09 %.

recordando que los periodos serían de 6 años…