Si diseña un equipo para transmitir el tono "la" de 440Hz, debe tomar en cuenta que no siempre es posible obtener una expresión matemática "sencilla" de una señal.
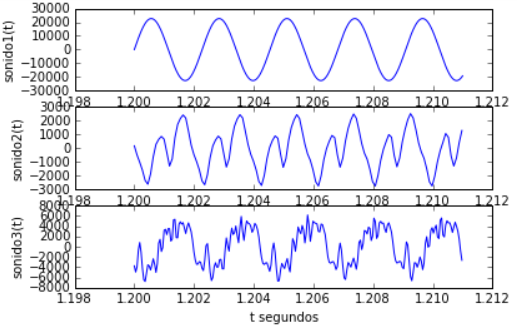
Escuche los siguientes sonidos, vea sus gráficas y realice sus observaciones:
-
-
-
- Proponga algunas expresiones matemáticas para cada una de las graficas mostradas.
- ¿Que tienen en común cada una de las señales?
- ¿Que tienen de diferente?
-
-
Algoritmo en Python
Para obtener la gráfica de los sonidos, se leen los datos y frecuencias de muestreo de cada uno de los archivos.wav
# Señales analógicas import numpy as np import matplotlib.pyplot as plt import scipy.io.wavfile as waves # INGRESO archivo1 = '440Hz_44100Hz_16bit_05sec.wav' [muestreo1, sonido1] = waves.read(archivo1) archivo2 = '440Hz_piano.wav' [muestreo2, sonido2] = waves.read(archivo2) archivo3 = '440Hz_violin_A4.wav' [muestreo3, sonido3] = waves.read(archivo3) # SALIDA - Observacion intermedia print('archivo, frecuencia , dimensiones:') print('sonido1: ', muestreo1, np.shape(sonido1)) print('sonido2: ', muestreo2, np.shape(sonido2)) print('sonido3: ', muestreo3, np.shape(sonido3))
con lo que se obtiene:
archivo, frecuencia , dimensiones: sonido1: 44100 (220500,) sonido2: 11025 (16538,) sonido3: 22050 (98160,)
Nota: si el archivo.wav tiene etiquetas, se descartan para el ejercicio. por lo que se presenta una advertencia "WavFileWarning".
c:\python34\lib\site-packages\scipy\io\wavfile.py:179: WavFileWarning: Chunk (non-data) not understood, skipping it. WavFileWarning)
Se observa que:
- todos los "sonidos" son monofónicos,
- las frecuencias de muestreo de cada archivo son diferentes
- las dimensiones de cada "sonido" o cantidad de muestras indican una duración diferente
Se recomienda escuchar nuevamente cada sonido y decidir el intervalo de observación para las gráficas. Se propone usar una ventana de observación o fragmento desde de los 1.2 segundos por 11 milisegundos.
Se extraen los fragmentos de cada sonido y se determinan los tiempos a los que corresponden basados en cada dt, con lo que se grafican los fragmentos.
# PROCEDIMIENTO # ventana de observación inicia = 1.2 termina = 1.211 canal = 0 # Extraen los fragmentos de sonido dt1 = 1/muestreo1 t1 = np.arange(inicia,termina,dt1) muestras = len(t1) fragmento1 = sonido1[int(inicia/dt1):int(inicia/dt1)+muestras] dt2 = 1/muestreo2 t2 = np.arange(inicia,termina,dt2) muestras = len(t2) fragmento2 = sonido2[int(inicia/dt2):int(inicia/dt2)+muestras] dt3 = 1/muestreo3 t3 = np.arange(inicia,termina,dt3) muestras = len(t3) fragmento3 = sonido3[int(inicia/dt3):int(inicia/dt3)+muestras] # SALIDA # grafica plt.subplot(311) plt.plot(t1,fragmento1) plt.ylabel('sonido1(t)') plt.subplot(312) plt.plot(t2,fragmento2) plt.ylabel('sonido2(t)') plt.subplot(313) plt.plot(t3,fragmento3) plt.ylabel('sonido3(t)') plt.xlabel('t segundos') plt.show()

Una vez obtenidas las gráficas, realice observaciones adicionales a cada una de las señales de sonido:
1.
2.
3.
Pregunta:
Para la nota musical "la", ejecutada en un violin tradicional tradicional de madera, ¿tendrá la misma forma de señal siempre?.
Considere las siguientes situaciones:
a. Tocada por diferentes músicos
b. en diferentes lugares
c. en diferentes días
Tarea
Buscar la nota "La" en otros instrumentos en formato.wav. De ser necesario realizar observaciones adicionales.
Referencia: Lathi 1.3.2 pdf/p.63, Estándar ISO16, Frecuencias de afinación de un piano
